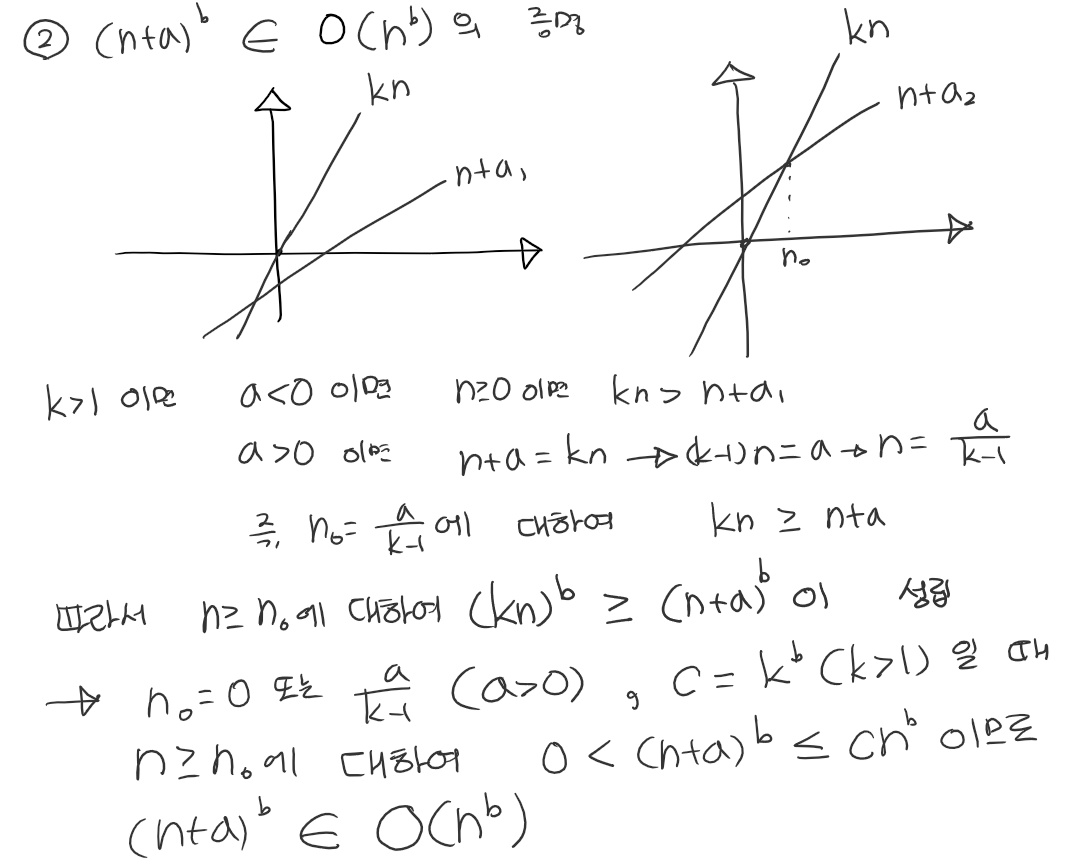
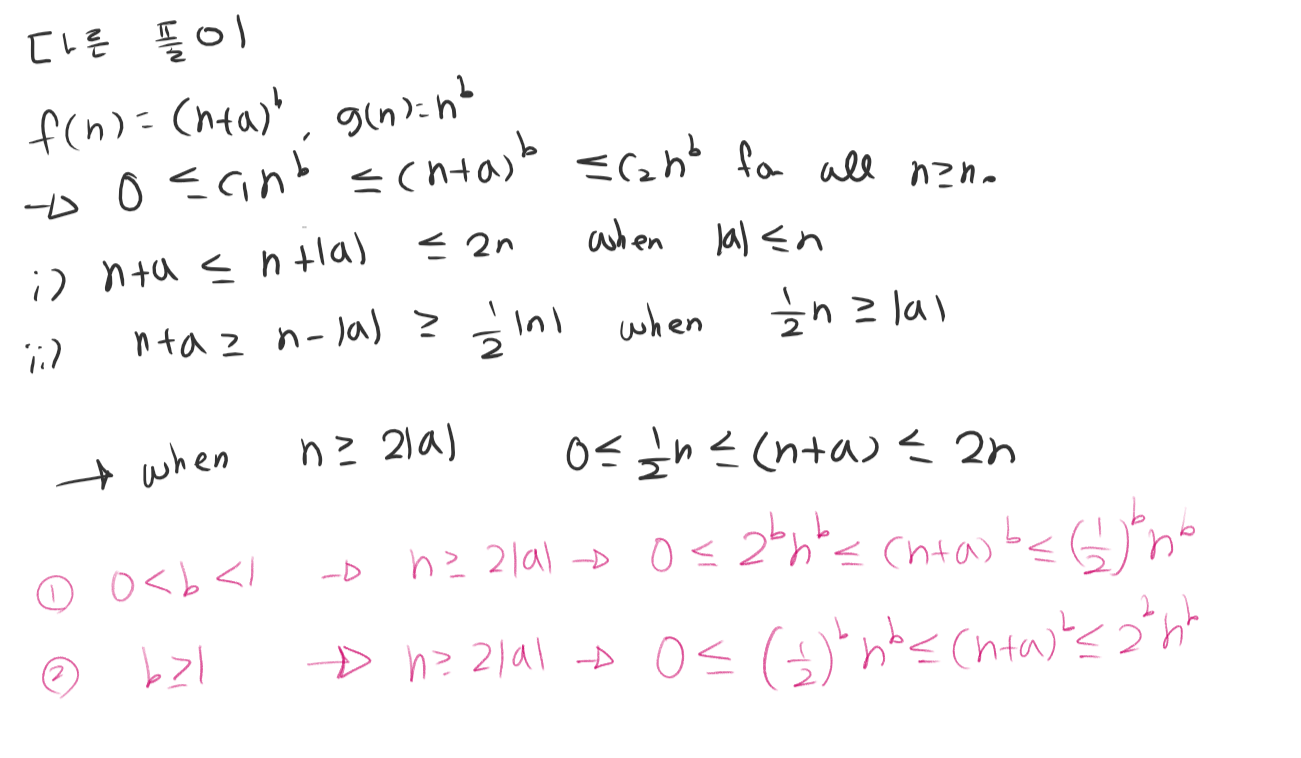알고리즘의 효율성은 차수로 간략하게 판단할 수 있다.
이를 Asymptotic efficiency of Algorithm이라 하는데 Asymptotic은 점근적임을 뜻한다.
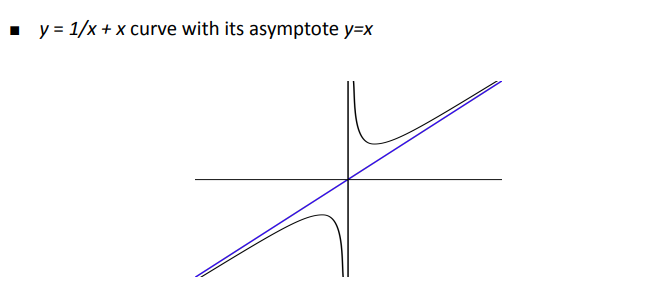
(고등 수학에서 배운 '점근'선)

차수에 따른 효율의 순서는 위와 같다.
이를 직관적으로 시간으로 비교해보면 다음과 같다.
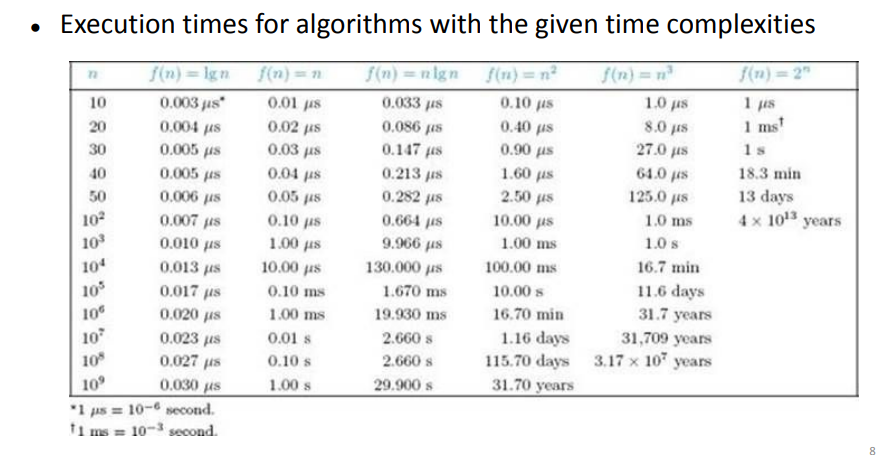
Big O notation으로 Upper Bound를 비교할 수 있는데 그 정의는 다음과 같다.
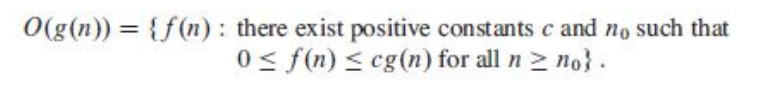
즉, f(n)이 n_0이상일 때, 0보다 크고 cg(n)보다 작게 하는 상수 c와 n_0가 존재하면 f(n)은 O(g(n))에 속한다.
ex.
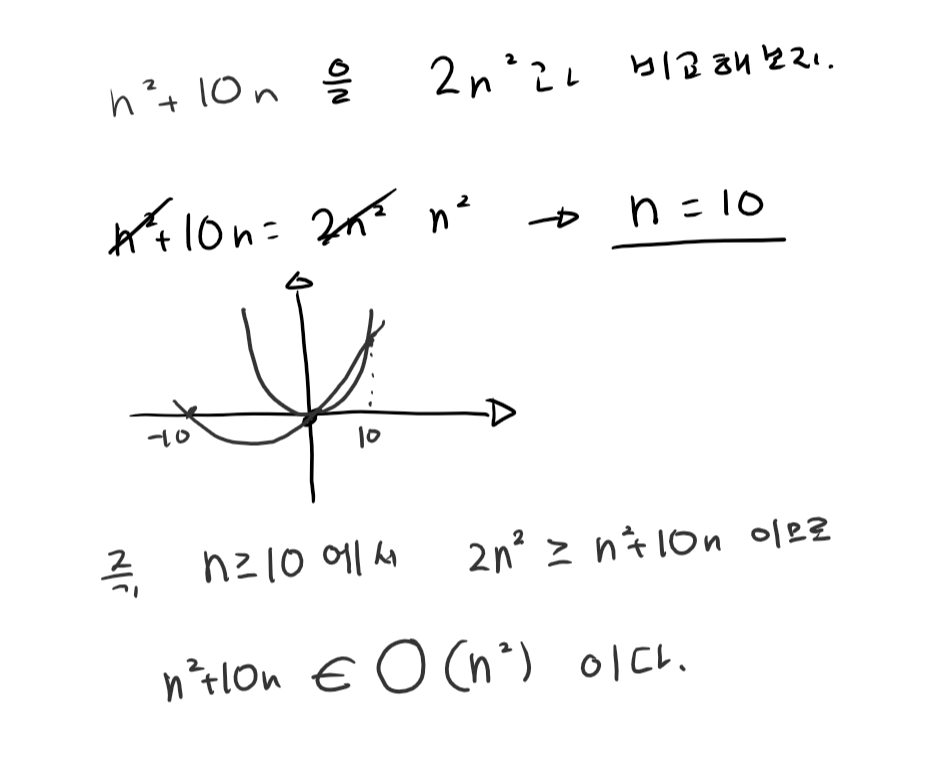
(0보다 크다는 조건이 빠졌지만 n^2 + 10*n 이 O(n^2)에 속함의 증명은 위와 같다.
정의상으로 n^2은 O(n^2 + 10n)에 속한다.
그러나 우리에게 중요한 것은 차수이므로 O(n^2 + 10n)과 같이 표기하지는 않는다.
또한 정의상으로 n은 O(n^2)에 속한다.
하지만 일반적으로 n은 O(n)이라 한다.
일반적으로 Upper Bound의 차수를 비교하기 위함인데 둘의 차수가 같지 않기 때문이다.
이는 뒤에서 비교하는 Big-theta 표기법으로 해결한다.
그럼 2^(n + 1)의 Big-O는 2^n 이 될 수 있을까?
될 수 있다. -> c = 2, n_0 = 1
2^(2n)의 Big-O가 2^n은?
이는 안된다.
2^(2n) = 4^n이므로 차수가 2^n보다 크다.
단순히 (2^n) (2^n)이라 보면 당연히 c 2^n을 무조건 추월한다.
주어진 함수들이 O(n^2)에 속하는지 판단해보자.

그리고 Upper Bound를 비교하는게 있으면 Lower Bound를 비교하는 것도 있고
이가 바로 Omega - notation이다.
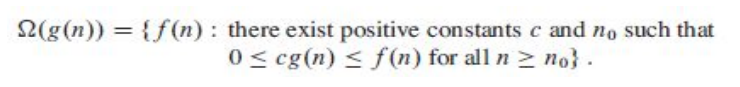
이를 점근적 하한이라고도 한다.
예제들




그리고 g(n)이 f(n)의 lower bound이자 upper bound이면 차수가 같은 것인데 이를 Big - theta라 한다.
이 Big - theta로 함수의 차수를 판단할 수 있다.
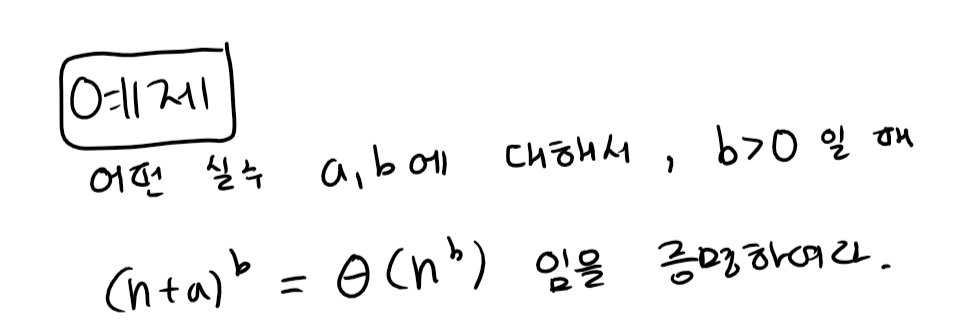
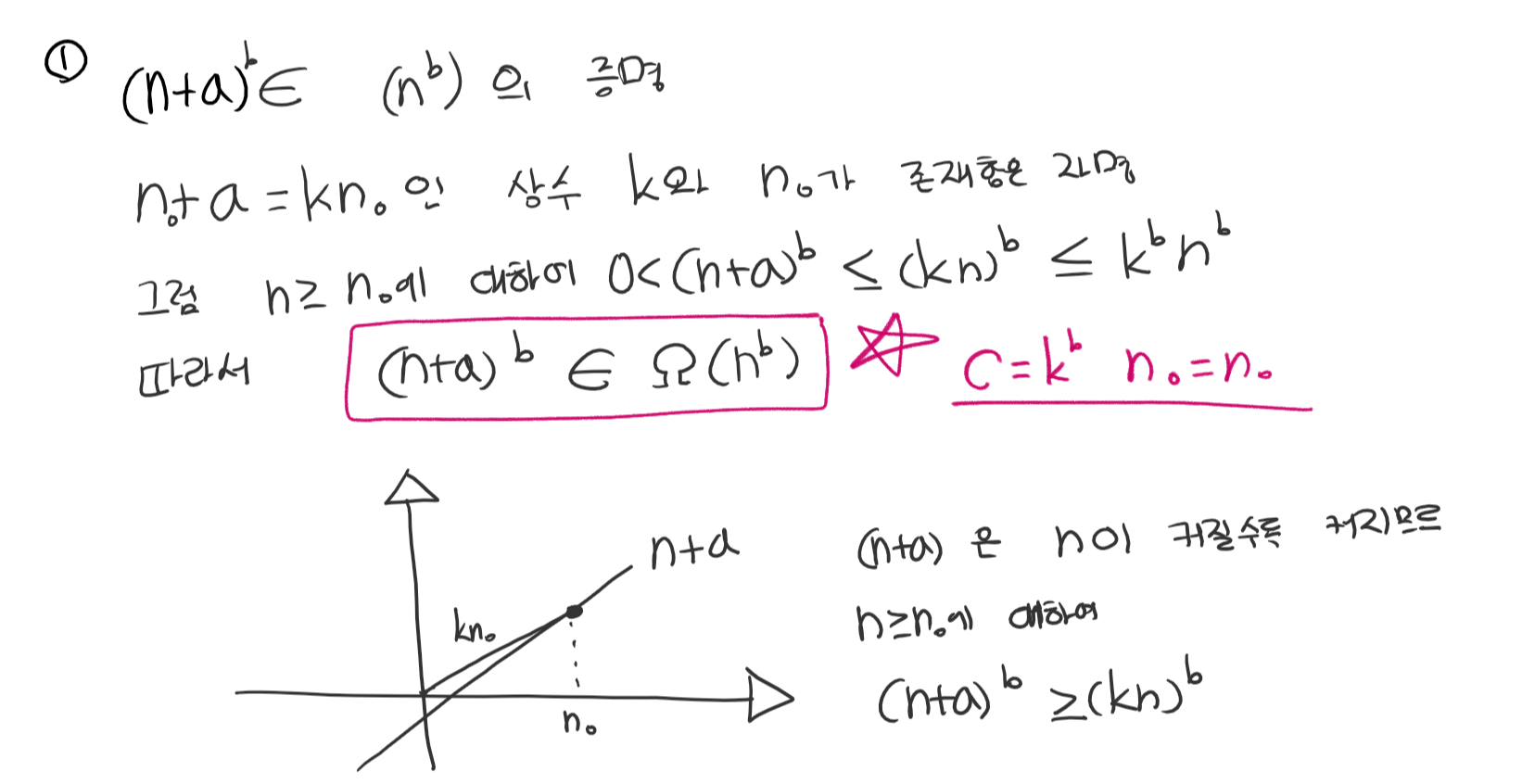
(위에는 k < 1 이라는 조건이 필요하다.)