학교 수업 - 알고리즘

삽입 정렬 코드이는1\. 처음에 한칸은 정의상 정렬되어 있는 상태이다. - 초기 조건 성립이미 정렬되어 있는 N칸에 하나를 더 삽입하면 이도 정렬되어 있다. - 유지 조건 성립N칸을 모두 정렬하면 종료 - 종료 조건 성립\-> 따라서 이는 합당한 알고리즘임을 알 수 있

이 그림을 참고하면 위와 같이 병합정렬의 연산횟수를 귀납적으로 나타낼 수 있는데 이는 수식으로도 다음과 같이 증명할 수 있다.

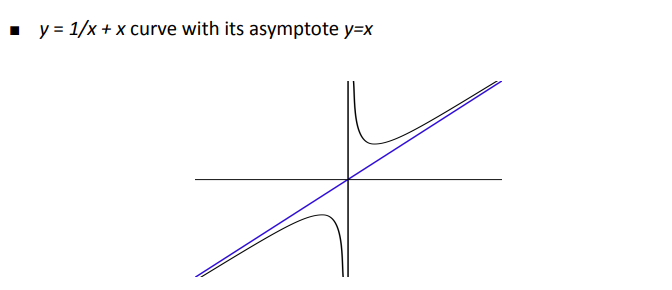
알고리즘의 효율성은 차수로 간략하게 판단할 수 있다.이를 Asymptotic efficiency of Algorithm이라 하는데 Asymptotic은 점근적임을 뜻한다.(고등 수학에서 배운 '점근'선)차수에 따른 효율의 순서는 위와 같다.이를 직관적으로 시간으로 비교

코드분할 정복의 분석

Substitution Method 복습재귀식 : T(n) = 2T(n/2) + n -> 병합정렬의 재귀식이다.추측 : T(n) = O(n logn)귀납에 의해 증명해야할 것 :T(n) <= cnlog n 이 어떤 상수 c > 0에 대해 만족해야 함먼저 basis

예제1내 풀이예제2풀이

pseudo codeBFS(G, s)for each vertex u (G.V에서 s를 제외한 모든 노드) u.color = WHITE; u.d = MAX; u.prev = NULL; s.color = GRAY; s.d = 0; s.prev =

https://m.blog.naver.com/ndb796/221234424646을 참고하여 공부 목적으로 작성한 글로 더 자세한 설명은 해당 글을 참고하여 주세요.이를 최소 거리를 배열을 모두 돌며 찾아내면 n짜리 배열을 n번 도므로 시간 복잡도는 O(V^2)

https://www.acmicpc.net/problem/1753 이를 다익스트라 알고리즘을 통해 풀어볼 것이다. 이 문제를 풀기 위해 필요한 것은 그래프 -> 정점이 20000개이므로 $$20000^2$$개의 성분이 필요한 인접행렬 방식 보다는 인접리스트 방식으로

![](https://velog.velcdn.com/images/honeyricecake/post/f9b270f8-97cd-4d46-8880-e

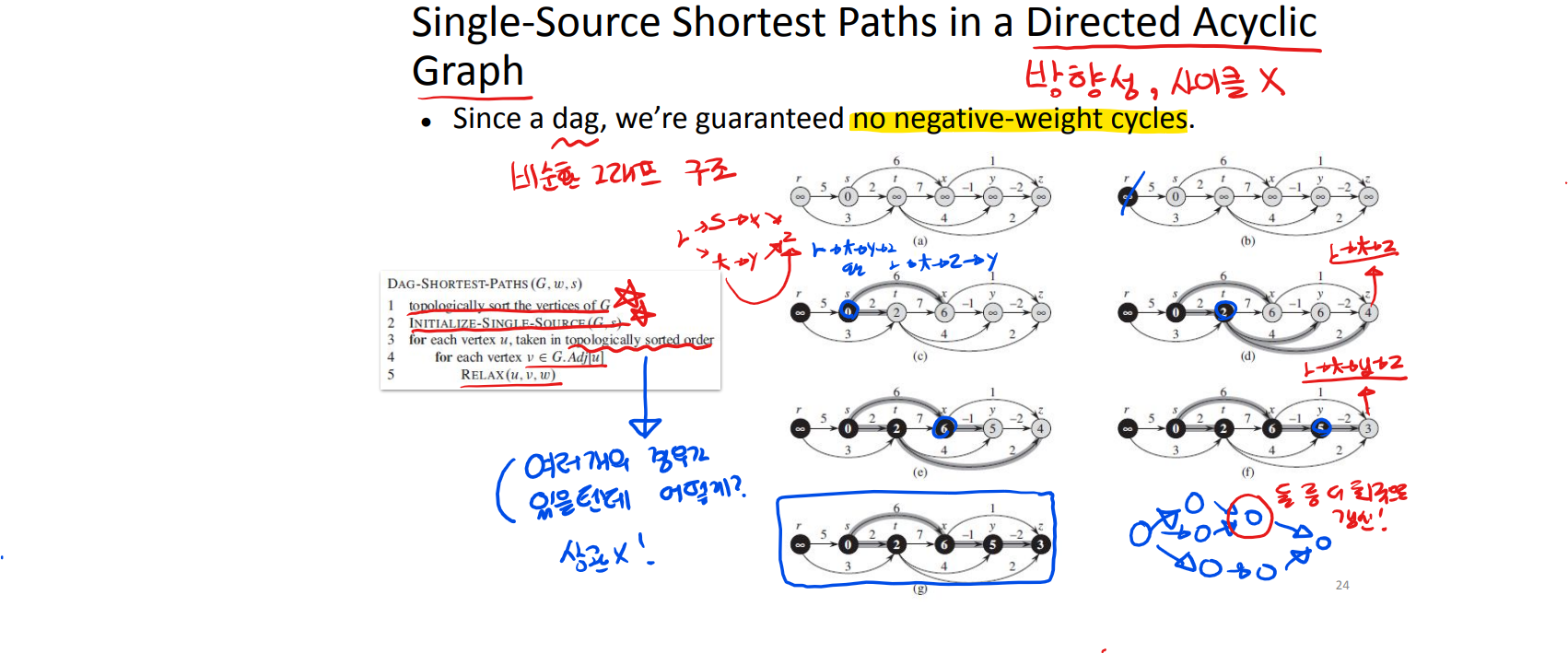
이러한 과정 반복!!1 -> 2 경로 출력 : pi(1,2) = 3pi(1,3) = 4pi(1,4) = 5pi(1,5) = 1pi(1,1) print 1따라서 1 , 5 , 4 , 3 , 2 출력확인 : -4 + 6 + -5 + 4 = 1, 경로를 따라가며 구해진 최단

앞의 내용 요약

너무 당연한 이야기이다. two free vertices를 연결하면 당연히 매칭수는 1증가XOR : 다르면 1 같으면 0 -> 매칭에 포함되는 path는 0으로 매칭에 포함되지 않는 path는 1로 !

주어진 입력이 참인지 거짓인지를 다항시간에 비결정론적으로 해결할 수 있으면 NP 알고리즘이다.즉, 비결정론적 튜링 기계 (한번에 결정할 수 있는 상태가 여러개)가 다항시간에 검증할 수 있는 알고리즘이 NP 알고리즘이다.NP의 또 다른 정의로는 다항 시간에 결정론적으로

Array(또는 리스트)는 가장 많이 사용하는 데이터 구조 중 하나이다.그래서 내부 구현 방법을 알고 써야 써도 괜찮은 상황과 더 효율적인 다른 구조를 써야할 상황을 구분 가능하다.기본 배열(Array)는 초기화할 때 크기가 지정되고 그 크기로 고정된다.데이터 크기를