




주어진 입력이 참인지 거짓인지를 다항시간에 비결정론적으로 해결할 수 있으면 NP 알고리즘이다.
즉, 비결정론적 튜링 기계 (한번에 결정할 수 있는 상태가 여러개)가 다항시간에 검증할 수 있는 알고리즘이 NP 알고리즘이다.
NP의 또 다른 정의로는 다항 시간에 결정론적으로 검증 가능(verifiable)한 문제들의 집합이다.
자세히 살펴보자면 어떤 결정 문제 X에 대해 어떤 입력과 입력 크기의 어떤 다항식으로 표현되는 크기를 갖는 증거(certificate)를 함께 제공받았을 때, 이를 다항 시간에 결정론적으로 검증하는 알고리즘이 존재하면 NP에 속한다.
검증 가능하냐 를 쉽게 말하자면 검산가능하다는 것이다.
예를 들어 헤밀토니언 사이클의 경우, 어떤 경로가 이 그래프의 헤밀토니언 사이클이다 라는 '증거'를 받았을 때, 이가 정말로 헤밀토니언 사이클의 증거인지는 O(n)에 검증가능하다.
이렇게 다항시간에 검증가능한 문제들을 NP문제라 한다.


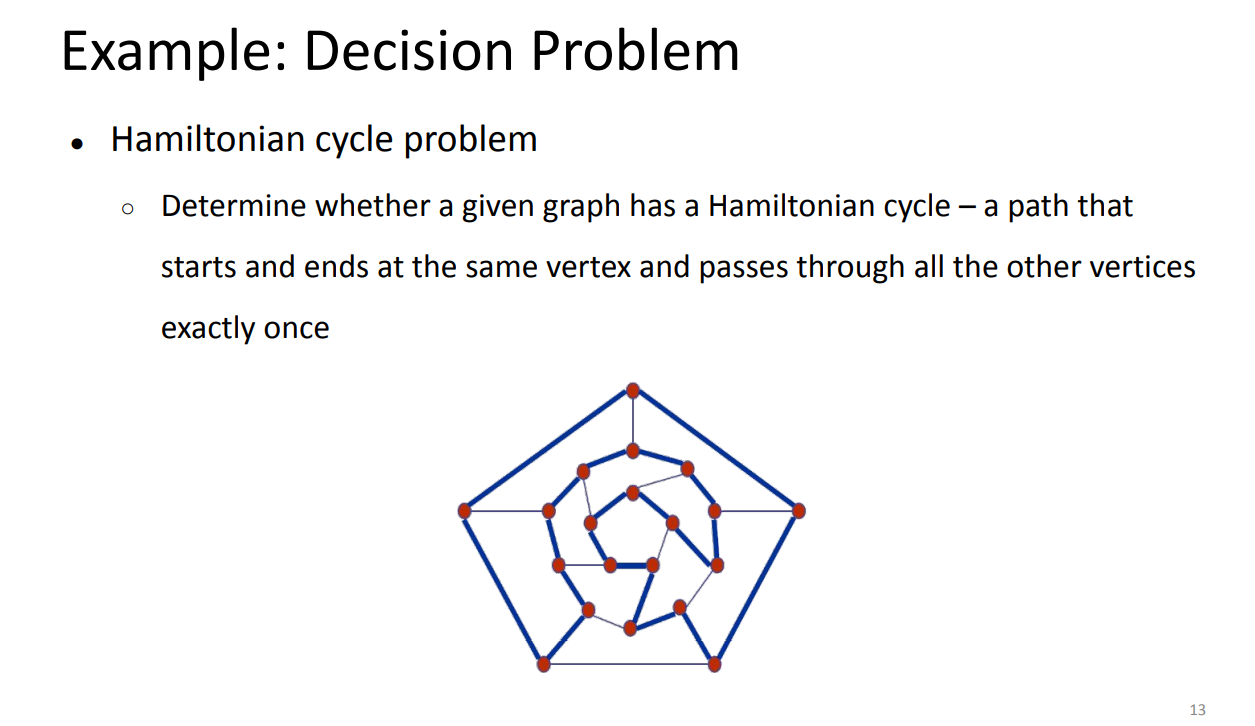

한 지점에서 모든 지점으로 이동하는 비용이 모두 주어졌을 때, 모든 지점을 한번만 방문하고 다시 원래 지점으로 돌아오는데 최소 비용이 드는 경로 구하기
이후 NP완전문제의 정의에 대해서는 이 포스트를 참고하였음울 밝힙니다.
https://gazelle-and-cs.tistory.com/74?category=877236
이미 우리는 P가 NP에 속한다는 것을 알지만 문제는 반대 방향이다.
따라서 NP문제들이 갖는 특징을 규명해 NP가 P인지를 찾고자 노력하였는데 그 결과, 어떤 특정 문제들은 그 자체로 NP에 속하기도 하지만 다른 모든 NP이 문제들에 비해 "어렵다"는 것을 보일 수 있었다. 또한 그 문제들 중 아무 하나만 P에 속한다는 것을 보인다면 P = NP라고 결론을 내릴 수 있다는 것을 알게 된다.
(반대로 P에 속하지 않는다는 것을 보이면 그 자체로 이미 P는 NP의 진부분집합임을 보이는 것이다.)
이를 NP완전문제라 한다.

NP완전은 최적화 문제가 아닌 결정 문제에 적용된다.



