기술블로그에서 서비스를 개선하거나, 새로운 기능을 추가하여 배포할 때 AB 테스트 기반으로 의사결정한다는 말을 자주 접한다. 구체적으로 어떤 상황에서 많이 쓸까?

언제 AB 테스트를 쓸까?

• 유저의 클릭율이 높은 썸네일이 뭘까? (ex. 유튜브, 넷플릭스)
• A 기능의 UI를 개선해볼까?
  • 전환율을 높이려면 총 4가지 UI 후보 중 어떤 후보를 선택할까?
  • 전환율이 0.3% 개선되었다면 이게 얼마나 영향이 있는 개선인가?
• B 기능을 추가하면 유저의 구매전환율이 높아질 것 같은데, 실제로 그럴까 or 예상치 못한 불편함을 주진 않을까

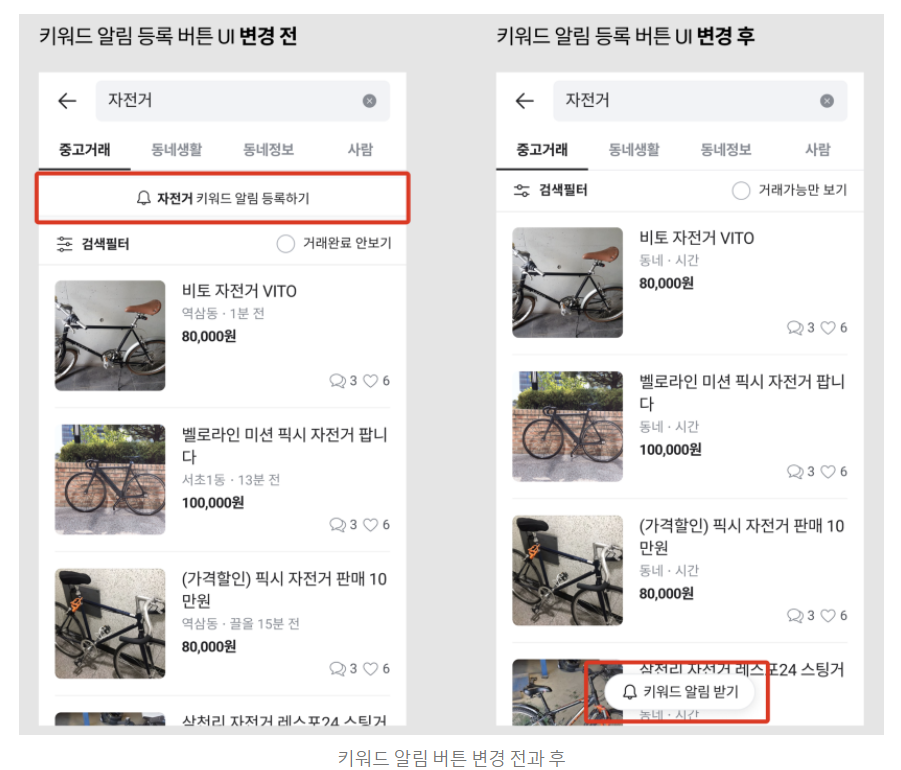
위 그림은 당근마켓 블로그 에서 소개한 키워드 알림 버튼의 위치를 변경했던 예시다. 왼쪽이 기존 방식이고, 오늘쪽이 변경된 모습이다. 검색 결과 상단에 키워드 등록, 검색 필터, 거래 완료 안 보기 기능 등이 모여 있는 것이 복잡하다고 판단하여 유저의 탐색에 방해되지 않도록 서비스 UI를 개선하려 했다고 한다.

ABCD 테스트는 어떻게?

위 그림 예시처럼 두 가지 후보 중 하나를 골라야할 때, t-test로 실험을 설계하면 통계적 유의성을 검증하며 더 나은 후보를 선택할 수 있다. 그런데 만약 후보가 3개 이상일 때는 어떻게 실험을 설계할까? 이번 글에서는 AB 테스트의 실험 대상이 A와 B 두 집단만 있는 것이 아니라 A,B,C,D 처럼 여러 여러개의 후보가 있을 때, Muticlass AB Test 실험 설계 과정은 일반적인 AB 테스트와 어떤 차이점이 있는지 작성했다.

1. 예시 : 쿠폰 디자인 개선하기

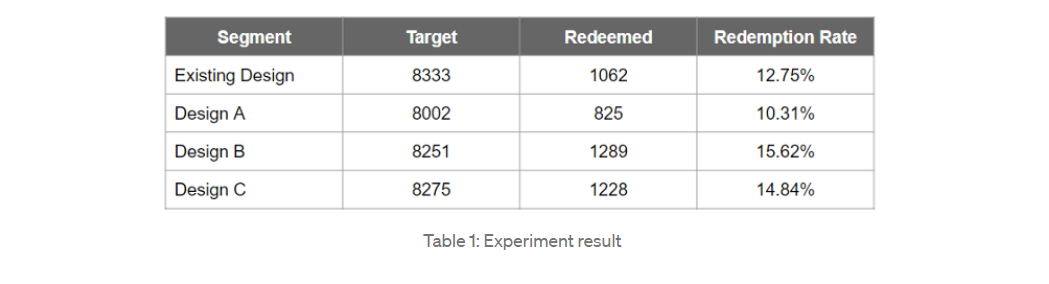
유저에게 프로모션 쿠폰을 뿌린 다음, 유저가 그 쿠폰을 구매에 이용하는 비율을 쿠폰 환수율(Redemption Rate)이라고 부른다. 쿠폰 환수율을 높이기 위해 디자인 UI를 개선하고자 한다. 다음과 같은 후보가 나왔다.

• 기존 Design
• Design A
• Design B
• Design C

redemption rate을 측정하는 방법은 다음과 같다.
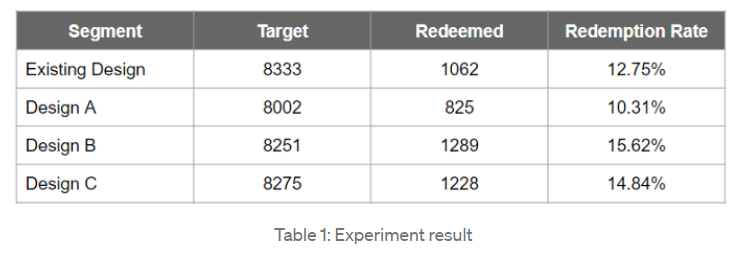
정해진 실험 기간동안 총 4 가지 후보 중 랜덤하게 디자인을 노출하고 각 유저 그룹마다 총 유저수(Target), 쿠폰 사용 수(Redeemed)를 기록한다. 분모를 Target, 그리고 분자를 Redeemed 으로 하여 Redemption Rate을 기록했고 그 결과는 다음과 같다. (이 예시는 이 곳에서 가져왔다.)

• Table 1
  

2. 실험 설계

실험 목적

• 디자인 UI 를 개선해서 기존보다 쿠폰 환수율(Redemption Rate) 높이기

유의수준 정의

• 유의수준은 귀무가설을 기각할지 여부 결정하는 기준으로, 실험 결과인 p-value가 유의수준보다 작으면 귀무가설을 기각하고, 크면 기각하지 않는다.
• 따라서 유의수준은 p-value를 계산하기 이전에 미리 정한다. 보통은 유의수준을 0.05로 설정한다.

실험1. 모든 디자인에서 쿠폰 환수율이 동일한가?

• 귀무가설 : 모든 디자인에서 쿠폰 환수 비율이 동일하다.
• 대립가설 : 적어도 하나의 디자인의 쿠폰 환수 비율 다르다.

샘플로 수집한 쿠폰 환수 여부 데이터는 categorical 변수이다. (Redeemed / not Redeemed) 따라서 두 개 이상 그룹의 categorical 변수의 분포를 비교하는 테스트인 Chi-Squared Homogeneity Test를 사용한다.

1. (Redeemed, not_Redeemed) 를 컬럼으로 하는 DataFrame 생성

import pandas as pd

target = [8333, 8002, 8251, 8275] # existing, A, B, C
redeemed = [1062, 825, 1289, 1278]

not_redeemed = [] # target - redeemed
for a, b in zip(target, redeemed):
    not_redeemed.append(a-b)

data = pd.DataFrame({'redeemed' : redeemed, 'not_redeemed' : not_redeemed})

2. Chi-Squared Homogeneity Test

from scipy.stats import chi2_contingency
# ref : https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html

stat, p_value, df, expected = chi2_contingency(data)
print(stat, p_value)
#### 결과 : 131.88996393138655 2.117192550458385e-28

테스트에서 사용할 검정통계량은 귀무가설 하에서 Chi-Squared 분포를 따르고, scipy.stats 라이브러리를 통해 검정통계량 값(stat)과 이에 해당하는 p-value 를 구할 수 있다. 결과를 보면 p-value값이 유의수준(0.05)보다 낮다. 따라서 귀무가설이 기각된다.

결론적으로 모든 디자인의 쿠폰 환수율이 같지 않다고 할 수 있다. 적어도 하나의 디자인이 쿠폰 환수율이 다르다고 판단하고 다음 스텝으로 넘어간다.

(만약 이 단계에서 귀무가설이 기각되지 않는다면? 다음 스텝으로 넘어가지 않고, 기존 디자인 UI를 유지하는 결론을 내릴 수 있다.)

실험2. 어떤 디자인의 쿠폰 환수율이 가장 높은가?

쿠폰 환수율이 가장 높은 디자인 UI를 찾기 위해 t-test를 반복적으로 수행한다.

• 언제까지 반복?
  - 통계적으로 유의한(significant) 결과를 얻기 전까지 반복
• 순서는 어떤 기준으로 정함?
  - Table 1 에서 Design B > Design C > Existing Design > Design A 순으로 쿠폰환수율이 높았다. 실험 목적은 "쿠폰 환수율이 가장 높은 디자인"을 찾는 것이므로, 가장 높은 환수율을 기록했던 B가 C보다 환수율이 높은지부터 테스트한다.

1. "Design B vs Design C" One-tailed t-test

• 귀무가설 : 두 그룹의 쿠폰 환수율이 같다. (Design B = Design C)
• 대립가설 : 디자인 B의 쿠폰 환수율이 더 높다. (Design B > Design C)

비율을 비교하는 테스트이므로 t-test for proportion을 사용한다. 두 그룹의 샘플 사이즈가 충분히 크기 때문에 CLT(중심극한정리)에 의해 z-test for proportion을 사용한다.

from statsmodels.stats.proportion import proportions_ztest

stat, p_value = proportions_ztest([1289, 1228], # redeemed Design B vs Design C
                                  [8251, 8275], # target Design B vs Design C
                                  alternative='larger')
print(p_value)
### 결과 : 0.08079746727160886

검정통계량은 귀무가설 하에 z 분포를 따르고, statsmodels.stats.proportion 라이브러리를 통해 검정통계량 값(stat)을 구하고 이에 해당하는 p-value 를 구할 수 있다. 결과를 보면 p-value값이 유의수준(0.05)보다 높다. 따라서 귀무가설이 기각되지 않는다.

결론적으로 Design B와 Design C의 쿠폰환수율은 비슷한 수준이라고 말할 수 있다. (B가 C보다 쿠폰환수율이 높다고 말할 충분한 근거가 없다.)

(만약 이 단계에서 귀무가설이 기각된다면? Design B가 가장 높은 환수율이라고 결론내릴 수 있으므로 다음 스텝으로 넘어가지 않고 테스트를 마무리한다.)

• 참고 : t 분포 대신 z 분포를 쓸 수 있는 이유
  

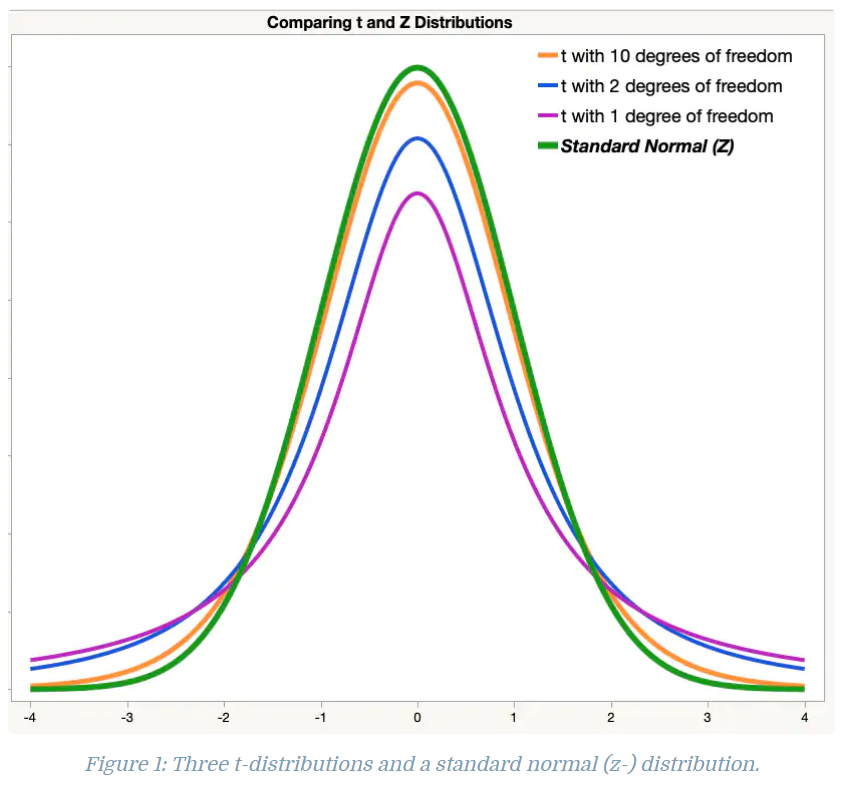
위 그림은 z-분포(초록색)과 자유도(degrees of freedom) 에 따른 t-분포를 그린 결과이다. 자유도는 샘플사이즈에 비례한다. t-분포는 자유도가 커짐에 따라 z-분포에 근사해간다고 알려져있다. 또한 CLT라는 개념이 있는데, 주어진 데이터가 어떤 분포를 따르건, 표본 평균(샘플을 표본이라고 한다)의 분포는 z분포에 근사해간다는 정리(Theorem)이다.

2. "Design BC vs Existing Design" One-tailed t-test

Design B와 Design C를 한 그룹으로 합쳐서 Segment BC라는 새로운 Segment를 만든다. 그리고 B와 C 다음으로 환수율이 컸던 Existing Design 과 비교하는 One-tailed t-test 를 수행한다.

• 귀무가설 : 두 그룹의 쿠폰 환수율이 같다. (Segment BC = Existing Design)
• 대립가설 : Segment BC의 쿠폰 환수율이 더 높다. (Design BC > Existing Design)

# Design B와 Design C를 한 그룹으로 합쳐서 Segment BC 
stat, p_value = proportions_ztest([1289+1228, 1062], # redeemed Segment BC vs Existing Design C
                                  [8251+8275, 8333], # target Segment BC vs Existing Design
                                  alternative='larger')
print(p_value)
### 결과 : 6.795738359244353e-08

p_value가 유의수준(0.05)보다 낮으므로 귀무가설이 기각된다. 통계적으로 유의한(귀무가설 기각됨) 결과가 나왔으니 t-test는 다음 스텝으로 가지 않고 종료한다.

결론적으로 Design B와 Design C는 기존 디자인에서보다 쿠폰 환수율이 높다고 말할 수 있다. 또한 Design B와 Design C의 쿠폰 환수율은 비슷한 수준이다. (=차이가 유의하지 않다.) 따라서 둘 중 무엇을 Best UI로 선택할 것인지는 의사결정권자에게 달려있다.

질문들

여기까지가 간단한 예시를 통해 알아본 Multiclass AB Test 이고, 정리하다가 생긴 몇 가지 질문들을 정리해봤다.

1. 왜 t-test를 여러번 하면 안 되는가? - 실험1

• 귀무가설 : 모든 디자인에서 쿠폰 환수 비율이 동일하다.
• 대립가설 : 적어도 하나의 디자인의 쿠폰 환수 비율 다르다.

예시처럼 디자인 후보가 4개라면, 이중 두가지를 고르는 경우의 수만큼 Multiple t-test를 수행하면 되지 않을까? 결론적으로 그렇게 하지 않는 이유는 테스트를 여러번 할수록 Type 1 Error가 증가하기 때문이다.

Type 1 Error = 귀무가설이 실제로 맞을 때, 귀무가설을 기각할 확률

4개의 그룹 중 2개를 고르는 조합의 수는 4C2=6 이다. 이렇게 총 6번의 t-test를 수행하기로 하고, 각각의 테스트는 서로 독립이며 유의수준은 0.05로 설정했다고 하자. 이 실험의 Type 1 Error를 계산하면 다음과 같다.

Type 1 Error
$= P$(6번의 테스트에서 귀무가설이 하나라도 기각 |귀무가설이 실제로 맞음)
$= 1 - P$(6번의 테스트에서 귀무가설이 모두 기각 안 됨 | 귀무가설이 실제로 맞음)
$= 1 - (1-0.05)^6$
$= 0.265$

※ 1번의 테스트에서 $P$( 귀무가설이 기각 안 됨 | 귀무가설이 실제로 맞음) $= 1-0.05$ 이다. 테스트끼리는 서로 독립이므로 테스트 숫자만큼 제곱한다.

하나의 테스트를 수행할 때는 Type 1 Error가 0.05였다. 반면 6번의 테스트를 수행하는 실험에서는 Type 1 Error가 0.265로 높아진다. 귀무가설을 잘못 기각할 확률이 5%에서 26.5%로 높아진다는 말이다. 따라서 실험을 설계할 때는 테스트를 최대한 적게 세팅해야지 Type 1 Error 증가를 방지할 수 있다.

2. 여러 집단을 비교하니까, ANOVA를 쓰면 안 되나? - 실험1

• 귀무가설 : 모든 디자인에서 쿠폰 환수 비율이 동일하다.
• 대립가설 : 적어도 하나의 디자인의 쿠폰 환수 비율 다르다.

실험 1에선 귀무가설과 대립가설을 정의하고 Chi-squared homogeneity test 로 실험 했다. 그런데 ANOVA 역시 여러 집단을 비교하는 통계 테스트 기법이다.

ANOVA : Analysis of Variance

• 2개 이상 그룹의 평균을 비교하는 테스트
• 필요한 가정(Assumption)
  • 정규분포 따라야함. (히스토그램으로 분포 확인 혹은 Q-Qplot 정규성 검증으로 확인)
  • 등분산성 만족
  • 각 관측치는 독립
• SST = SSW + SSB
  • SSW : 그룹 내부의 관측치와 그룹 평균의 차이를 Sum of Square
  • SSB : 그룹 평균과 전체 평균의 차이를 Sum of Square
• 검정통계량 F = {SSB/df_B} / {SSW/df_w} 는 귀무가설 하에, F분포를 따름

Chi-squared homogeneity test와 ANOVA의 차이는 무엇일까?

• 공통점 : 두개 이상의 그룹에서, 특정 변수의 분포가 동일한지 확인하는 테스트
• 차이점 : 그 변수가 Categorical 하다면 Chi-squared Test를, Continuous 변수가 포함되어 있다면 ANOVA 를 쓴다.

간혹가다 데이터 전처리 과정에서 Continuous 변수처럼 보이지만 Categorical 변수인 경우가 있다. 예를 들어, 값이 0 또는 1로 구성되어 있지만 0보다 1이 큰 것이 중요하다는 숫자로서의 의미가 없다면, 해당 변수는 Categorical 변수이다.

마무리하며

1. 가정의 중요성

테스트를 선택하기에 앞서, 테스트의 가정이 맞는지 확인하는 것이 중요한 것 같다. 예를 들어, 특정 기능 도입이후 구매 전환율을 기록했다고 하자.

아래 테이블에서, 구매 전환율은 대조군(Control)은 2%, 실험군(Test)에서 1.7% 로 0.3% 가량 감소했다. 이 0.3% 감소가 통계적으로 유의한 감소인지 확인하기 위해 테스트를 진행하려고 한다.

• Table 2 (출처)
  

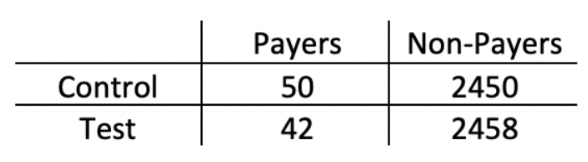
주어진 데이터는 Payers와 Non-Payer 사이의 불균형이 심하다. 이렇게 카테고리가 불균형하거나 특정 그룹의 샘플 사이즈가 매우 작은 경우에는 Chi Square Test를 쓰지 않고 Fisher Exact Test를 쓴다. (Chi Square Test 가정 : 데이터가 불균형하지 않고 샘플 사이즈가 충분히 커야함.)

Python은 라이브러리가 잘 되어 있어서 AB Test를 할 때 검정통계량의 수식이 어떻게 구해지는 지에 대한 내용은 크게 중요하지 않아 보인다. 대신, 사용하려는 테스트의 가정이 주어진 샘플 데이터에서 만족되는지 체크하는 절차가 중요한 것 같다. 위 예시처럼 불균형이 심한 데이터의 경우, Chi Square Test의 가정을 만족하지 못하므로 대안으로 Fisher Exact Test를 써야한다.

2. 실험 목적의 중요성.

Multiclass AB Test에서 실험을 최대한 적게 하려면 실험 목적을 구체적으로 설정하는 것이 중요하다는 것을 알게 되었다. 위의 예시에서 "만일 4가지 디자인의 쿠폰 환수율 순위"를 구하는 것이 목적이었다면, 불필요한 t-test를 추가로 수행하여 Type 1 Error가 높아졌을 것이다.

출처

1. Multiclass AB Testing

2. ANOVA in ABC test

3. Parametric Test vs Non Parametric Test