CS224W 3.1 Node Embeddings

1. 배경

• 전통적인 Graph 구조의 ML에서는 수동으로 Feature를 생성하고 학습해야함.
  • Lecture 2에서 다뤘던 내용들

    노드 예측을 위한 Feature: 노드의 차수, 노드중심성,
    에지 예측을 위한 Feature: distance(최단경로), neighborhood 기반....
    그래프 예측을 위한 Feature: Graph kernel(Graphlets, WL)...

• 네트워크 구조에서 Feature를 자동으로 학습하고 싶음

---

2. Graph Representation Learning

• Graph ML에서 효율적이며 태스크 독립적인 Feature learning을 하는 것이 목적

---

3. Embedding

• Task : 그래프에서의 노드를 임베딩 스페이스로 매핑하는 것

• Example : 두 노드가 하나의 에지로 연결되어 가깝다면, 임베딩 유사도는 네트워크에서의 유사도와 근사값을 갖는다

• 활용 : 다운스트림 예측작업에 활용 (임베딩 스페이스로의 표현을 Feature로 사용)
  이상탐지, 클러스터링, 그래프 분류, 링크예측 등에 사용

  💡Downstream task
  최종적으로 해결하고 싶은 문제를 의미합니다.
  Pre-train 방식으로 학습을 시켜 모델 생성한 후,
  Fine-tuning을 통해 모델을 업데이트 $\leftarrow$ 이를 의미할수도 있다고 하네요.

  💡Graph representation learning 접근론의 분류

  • Classical methods
    • Dimension-reduction-based-methods : PCA, LDA...
    • Random-walk-based methods : DeepWalk, node2vec
    • Matrix-factorization-based methods : GraRep, HOPE, ...
  • Emerging methods
    - Neural-network-based methods : GCN, Signed GCN...
    - Large Graph Embedding methods : GPNN, LINE ...
    - Hypergraph embedding : HGNN
    - Attention Graph embedding : GAT, AttentionWalks
    - Others : GraphGAN, GenVector
    💡참고:Graph representation learning:A Survey

---

4. Deepwalk (2014 ~ 2015)

4.1. Encoder & Decoder

4.1.1. 용어 정의

• Encoder : 노드($v$)를 임베딩 벡터($z_v$)로 매핑

  $Enc(v)=z_v$
  v:입력 그래프의 노드, z: d차원읜 노드 임베딩 벡터

• Similarity Function : 네트워크 상에서의 유사도 함수 정의 (# of hops)
• Decoder : 임베딩 벡터($z_k$)를 유사도 점수(Similarity score)로 매핑

  $similarity(u,v) \approx z_v^Tz_u$

• Optimization : 인코더의 파라미터를 최적화 (적합한 임베딩표현을 찾기 위함)

4.1.2. Simplest encoding approach

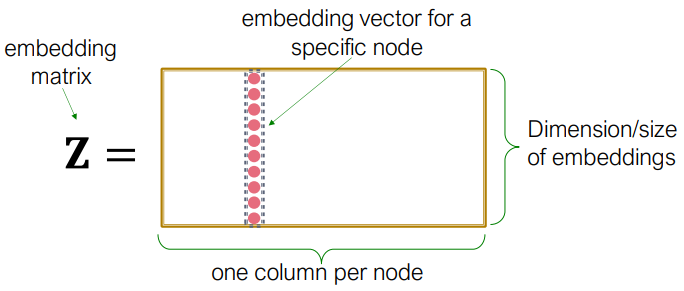
• "Shallow" Encoding : 인코더 = 단순한 Embedding-lookup
  • 개별 노드를 유일한 임베딩 벡터로 표현하는 것

    $ENC(v) = z_v = Z\cdot v$
    $Z \in R^{d\times|V|}$, matrix, 각 칼럼은 노드임베딩을 나타냄
    $v \in \mathbb{I}^{|V|}$, indicator vector, 한 칼럼에서 v제외 모두 0

• 👇그림 설명
  

4.1.3. Framework Summary

• Encoder + Decoder Framework
• Shallow Encoder : 임베딩 룩업 사용
• Parameters to optimize : 모든노드에 대한 노드임베딩 z를 포함하는 Z
• Decoder : node similarity 기반
• 목적함수 : 유사한 노드쌍 (u,v)에 대한 임베딩벡터의 내적을 최대화하는 것

  Node similarity는 어떻게 정의할까?
  서로 연결되어있는가? 이웃을 공유하는가? 유사한 구조를 가지는가?
  💡 random walk를 사용한 노드 유사도 정의를 사용함.
  💡 이 random walk 유사성을 측정하기 위해, 노드 임베딩을 최적화해서 사용.

4.1.4. 노드임베딩에 대한 참고사항

• unsupervised/self-supervised 방식임
  • 노드 임베딩의 목표값(label)을 제공하지 않음
• 이러한 임베딩은 태스크 독립적임
  • node label, node feature를 이용하지 않음
    노드가 사람이라면, 노드 특징이 될 수 있는 위치,성별,나이 등의 특징 활용x
  • 네트워크 구조 이외의 부가적인 정보를 활용하지않고, 네트워크 유사성 개념 포착
    어떤 태스크에도 사용할 수 있는 일반화된 임베딩을 고려한 방식