CS224W 3.2 Random Walk

1. Notation

1.1. 용어

• Vector $\mathbf{z}_u$ 찾고자 하는 목표
• Probability $P(v|\mathbf{z}_u)$ u에서 출발, v를 방문할 확률

1.2. non-linear function

확률밀도함수에 사용하기 위한 non-linear function

• Softmax function : 다중 분류에 사용 (보통 출력층 activation func.)

  $Softmax(z)_i=\frac{e^{z_i}}{\sum_{j=1}^{K}e^{z_j}}$

• Sigmoid function : 이진 분류에 사용 (보통 중간층 activation func.)

  $\sigma(x)=\frac{1}{1+e^{-x}}$

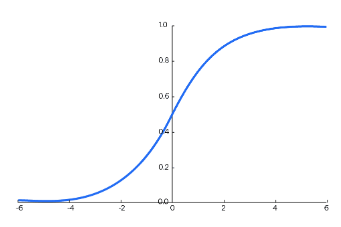
📌 참고
Softmax 함수는 Sigmoid 함수의 일반화
Odds $\rightarrow$ Logit(딥러닝의 raw출력) : 0을 기준 [$-\infin, \infin$]
Logit $\rightarrow$ Sigmoid : 상호 역함수 [0,1]
$Logit(y)=x \rightarrow y=\sigma(x)$
Sigmoid $\rightarrow$ Softmax : 다중클래스에 대해 일반화

2. Random-Walk

2.1. 개괄

• input : 그래프
• 로직
  • 1) 랜덤하게 이웃을 선택해서 그 이웃으로 이동
  • 2) 선택한 이웃에서 랜덤하게 이웃으로 이동...
  • 위 두 과정을 반복한 "노드들의 시퀀스"

2.2. Random-Walk의 Embeddings

• 유사성, 확률을 어떻게 정의할까? 👇

  $z_u^Tz_v \approx$ u와 v가 그래프 랜덤워크에서 동시에 발생하는 확률

• approach
  • 랜덤워크(무작위걷기!) 로직을 통해, 어떤 노드 u에서 v를 방문할 확률 추정 $P(v|u)$
  • 임베딩 최적화 임베딩 내적값이 필요함!

2.3. Random Walks의 Contribution?

• Expressivity : 노드 유사성에 대한 유연한 표현방식(확률론적 정의)
• Efficiency : 모든 노드를 학습할 필요가 없음. 동시발생하는 노드쌍만 필요

2.4. Unsupervised Feature Learning

• Intuition : 유사성이 보존되는 $d$차원의 노드 임베딩을 찾는 것.
• Idea : 그래프의 인근노드가, 임베딩 공간에서도 서로 가깝게 임베딩되도록 임베딩을 하자
• "가깝다"의 정의? = u의 이웃노드에 대한 정의

  $N_R(u)$ = u에서 시작한 랜덤워크 R에서 얻은 노드들

2.5. Feature Learning as Optimization

2.5.1. Notion.

• Input : G = (V, E)
• Objective : $f(u) = \mathbf{z}_u$
• Log-likelihood objective :

  $max_f \displaystyle\sum_{u\in V} logP(N_R(u) | \mathbf{z}_u)$

  • 관측치 : $N_R(u)$
  • 구하려하는 파라미터 : $\mathbf{z}_u$
  • 이 확률을 최대화하여 분포의 모수(파라미터) 예측

2.5.2. How to?

• 그래프의 노드 $u$에서 시작하는 짧은 고정 길이의 Random Walk 수행
• 노드 $u$로부터 랜덤워크로 방문한 노드들의 집합 $N_R(u)$를 생성
• 노드 $u$의 이웃 $N_R(u)$를 예측해서 임베딩을 최적화
• ❗최대우도법에 의해 최적화
• Loss function의 정의 : Negative Log likelihood 개념
  우도법은 값을최대화 > (-)부호를 통해 최소화 개념으로 전환

  $\mathcal{L} =\displaystyle\sum_{u\in V}\sum_{v\in N_R(u)}-log(P(v|\mathbf{z}_u))$
  👉 Loss를 최소화하는 임베딩 $z_u$를 찾아보자
  👉 $z_u$와 $z_v$의 내적을 최대화하면, Loss는 0에 가까워진다

• 직관 : 랜덤워크 동시발생 우도를 최대화하여, 임베딩 $z_u$를 최적화
• 랜덤워크 동시발생 우도(likelihood)의 정의

  $P(v|\mathbf{z}_u) =\frac{exp(\mathbf{z}_u^T\mathbf{z}_v)}{\displaystyle\sum_{n\in V}exp(\mathbf{z}_u^T\mathbf{z}_n)}$
  ✍ Why softmax? 다중클래스 분류문제로, 모든 노드들의 확률 분포를 정의하기 위함. 그러나 연산복잡도가 큼!

2.5.3. 연산복잡도의 문제

• Problem : node의 개수 $V$ 기준, complexity가 높음 : $O(|V|^2)$

  • 모든 노드에 대한 $Loss$를 구하긴 해야하기 때문에 $u\in V$를 줄일 순 없으나, softmax func.의 정규화를 위한 $n\in V$를 줄일 순 있지 않을까?
  • softmax의 정규화를 위해 모든 노드와의 내적연산을 거치는 부분에서 연산복잡도가 발생
  • ❓ 이 값의 근사치를 이용해서 연산을 개선할 수 없을까

• Solution : Negative sampling

  $log(\frac{exp(\mathbf{z}_u^T\mathbf{z}_v)}{\displaystyle\sum_{n\in V}exp(\mathbf{z}_u^T\mathbf{z}_n)} )$
  $\approx log(\sigma(\mathbf{z}_u^T\mathbf{z}_v)) - \sum_{i=1}^{k} log(\sigma(\mathbf{z}_u^T\mathbf{z}_v)), n_i\sim P_v$
  $\rightarrow$ 노드$u,v$가 주어졌을 때, 두 개의 노드가 서로 유사한가에 대한 이진분류문제로 전환(단, node의개수만큼 반복 *k회 수행)

  아래의 수식이 의미하는 것은 "노드 u, v가 유사하게 임베딩 되었을 확률-노드 u와 negative sampled된 노드(u와 유사하지 않을 것이라 판단된 노드.random walk에서 u 근처에 없는노드)이 유사하게 임베딩되었을 확률"로, 아래의 수식을 높게 학습시킨다는 것은 u와 v의 임베딩은 유사하도록, u와 negative sample된 다른 노드들의 임베딩은 유사하지 않도록 학습시킨다는 것을 의미함.
  아래의 수식에서의 sigmoid함수는 [0,1]확률화의 기능으로 도입
  참고:

📌참고 : 네거티브 샘플링

• 네거티브 샘플링은 전체 노드에 대한 내적값을 구하는 대신, 노드 $u$와 이웃하지 않은 노드 중 $k$개를 샘플링하여 사용함. 분자(앞)의 $\sigma$ 항은 $u$의 이웃노드와 계산되는 이웃노드일 확률로 최대화되며, 뒤의 $\sigma$ 항은 $u$의 이웃하지않은 노드와 계산되는 이웃노드일 확률로, 최소화되게 됨.

• 이 방법은 word2vec의 연산복잡도 개선 방식과 매커니즘이 동일. 문제의 정의를 아래와 같이 변경

• $V$에 포함된 모든 노드를 보지않고, $k$개의 별도 선별한 negative sample을 사용한다는 점도 다른 점입니다!

  word2vec
  AS-IS 'you'와 'goodbye' 맥락단어 입력이 주어질 때, 가운데에 나올 단어는 무엇입니까?
  TO-BE 'you'와 'goodbye' 맥락단어 입력이 주어질 때, 가운데에 나올 단어는 'say' 입니까, 아닙니까?
  Random walk
  AS-IS 입력 노드 "u"가 주어질 때, 이웃노드는 무엇입니까?
  TO-BE 입력 노드 "u"가 주어질 때, 'v'는 이웃노드입니까?

2.5.4. Negative Sampling

• negative sample을 어떻게 선별할까?
  • negative sample($k$개)로 선정될 확률 $\propto$ 노드의 차수
    빈도수가 높은 단어들은 범용적으로 활용되는 경우가 많기 때문에, 특정 노드와의 관계가 크지 않을 것이라는 직관
  • $k$의 값이 높아지면? negative event에 대한 bias를 발생시킬 수 있음
  • 일반적인 케이스 : $k=5 \sim20$

2.5.5. SGD (Stochastic Gradient Descent)

• 위 과정을 통해 Objective function에 대한 정리를 마쳤습니다.
• 그렇다면 어떻게 Loss를 최소화할 수 있을까요?
• Solution : 확률적 경사하강법(SGD)로 해결
  • vanilla GD
    • 경사도(미분)의 반대방향으로 이동하여, 수렴할 때까지 반복
    • $\mathrm{(i)}$ 단일 노드임베딩의 우도함수의 도함수(경사)를 계산
    • $\mathrm{(ii)}$ 경사의 (-)로 갱신 (한걸음의 폭은 learning-rate로 조정)
  • Stochastic(확률적) GD
    • 모든 단일노드에 대한 경사를 계산하지않고, mini-batch를 이용

(i) 경사도의 계산 : $\frac{\partial L^{(i)}}{\partial z_j}$ 의 계산
(ii) 모든 $j$에 대하여 $z_j$를 업데이트 : $z_j\leftarrow z_j-\eta\frac{\partial L^{(i)}}{\partial z_j}$

2.5.6. Random Walks Summary

• 그래프상의 각 노드에 대해 고정길이의 짧은 Random Walk를 수행
• 각 노드 $u$에 대한 $N_R(u)$를 생성
• SGD 방식을 통해 임베딩을 최적화 (네거티브 샘플링 방식을 이용하여 연산복잡도 문제 개선)

3. Random Walk를 수행하는 방법론

3.1. DeepWalk & Node2vec

• DeepWalk : 고정길이의 Random Walk, 편향되지않은 랜덤워크가 특징
• node2vec : Flexible, 편향된 랜덤워크를 사용
  • BFS를 통해 Micro view, DFS를 통해 Macro(global) view

3.2. Node2vec

3.2.1. Idea

• 노드 $u$에서 랜덤워크로 생성된 이웃 집합 $N_R(u)$를 생성하기 위해, 편향된 랜덤워크 R를 사용한다!
• 2개의 파라미터 사용
  • 이전방문 노드로 돌아가기 위한 확률 파라미터 $p$
  • 멀어지기 위한(Moving outwards) 확률 파라미터 $q$
    - 더 멀어지는 방향으로 (DFS) & 근처를 탐색하는 방향으로 (BFS)
    - $q$는 BFS와 DFS의 확률 비율
    
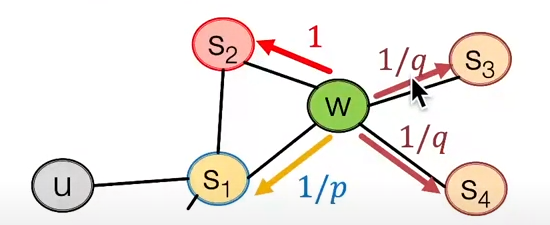
• $s_1\rightarrow w$ 로 이동했을 때, 다음노드를 선정하는 확률
  • $w\rightarrow s_1$ : $\frac{1}{p}$, 이전노드로 되돌아감
  • $w\rightarrow s_2$ : $1$, 동일한 거리를 유지하는 노드
  • $w\rightarrow s_3, s_4$ : $\frac{1}{q}$, 거리가 멀어지는 노드
  • 위 확률을 1로 정규화한다음, 확률에 의거하여 랜덤하게 진행방향을 선택함

    BFS-like walk : 낮은 $p$의 값
    DFS-like walk : 낮은 $q$의 값

3.2.2. 알고리즘

• (i) 랜덤워크의 확률 계산
• (ii) 각 노드 $u$에서 시작하여, 고정길이 $l$의 랜덤워크 시뮬레이션
• (iii) [Deepwalk와 동일] SGD를 이용하여 objective func.을 최적화

3.2.3 특징

• 선형 시간복잡도
• 알고리즘의 각 단계를 병렬처리 할 수 있음
• 단점이라면? 각 노드를 각각 학습해야한다는 점.
  • 노드의 개수가 많은 그래프일수록 임베딩 학습에 소요되는 자원👆

4. Summary

• Core idea : Input graph에서의 노드유사도를 반영할 수 있도록 노드를 임베딩
• 노드 유사도를 판단하는 방법들
  • Naive : 두 노드가 직접연결되어있다면 유사한것으로 판단
  • 개선(i) : 공통이웃을 공유한다면 유사한 것으로 판단
  • 개선(ii) : Random Walks 접근법 (3.2강에서는 이부분을 다룸)
• 모든 케이스에 적합한 방법론은 없음
  • node2vec는 링크예측보다 노드예측에서 더 좋은 퍼포먼스를 보임
  • random walk 방법론들은 제한된 수의 랜덤워크를 시뮬레이션하기 때문에 효율성이 좋음
  • 하지만 일반적으로는 각각의 애플리케이션에 적합한 노드유사도 정의를 선택해야함!