CS224W 4.4 Matrix Factorization and Node Embeddings

1. 개요

• 행렬분해와 노드유사도의 연결
  • 가장 단순한 형태의 노드유사도
    • 에지로 연결된 nodes $u, v$는 유사하다!
  • 이는 $\mathbf{z}_v^T\mathbf{z}_u=A_{u,v}$를 의미
    • 인접행렬에서의 $(u,v)$가 에지 연결을 의미하며, 노드 $u,v$의 벡터를 내적한 것이 유사도를 의미하기 때문
    • 두 노드가 유사하다면, 노드임베딩의 내적값이 1이 되어야함
  • 즉, 행렬관점으로는 : $\mathbf{Z}^T\mathbf{Z}=A$
    
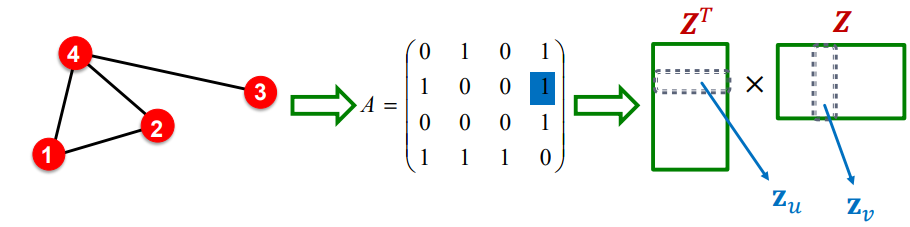
  • 즉, 인접행렬 A가 두개의 행렬로 행렬분해되었다고 볼수있음

2. 행렬분해

2.1. 가장 단순한 형태의 행렬분해

• 임베딩 차원 $d$는 일반적으로 노드의 개수 $n$보다 훨씬 작은 수임

  • 노드 100만개, 10차원의 임베딩 벡터를 생각해본다면
  • $A=\mathbf{Z}^T\mathbf{Z}$의 정확한 해를 찾는것은 불가능할 것

• 그러나 대략적으로 $Z$를 학습하는 방식으로 해를 찾을 수 있음

  • Objective

    $\displaystyle\min_Z||A-\mathbf{Z}^T\mathbf{Z}||_2$

    • Frobenius norm을 사용하여 $\mathbf{Z}$를 최적화
    • $A-\mathbf{Z}^T\mathbf{Z}$를 구하고, 제곱값을 합산
    • lecture 3에서는, l2 norm을 사용하지 않고, softmax 함수를 사용했음 (그러나 근사치를 구하려는 목표는 동일했음!)

• 결론 : 에지 연결에 의해 노드유사도를 정의하는 내적 디코더는 $A$의 행렬분해 표현과 동일함

2.2. Random walk-based similarity

• 앞 장에서 살펴본대로, DeepWalk나 node2vec에서의 노드유사도에 대한 정의는 보다 복잡한 형태를 갖게됨

• Deepwalk의 행렬분해:

  $\log(vol(G)(\frac{1}{T}\sum_{r=1}^{T}(D^{-1}A)^r)D^{-1})-\log b$

• 👇 자세한 설명

  

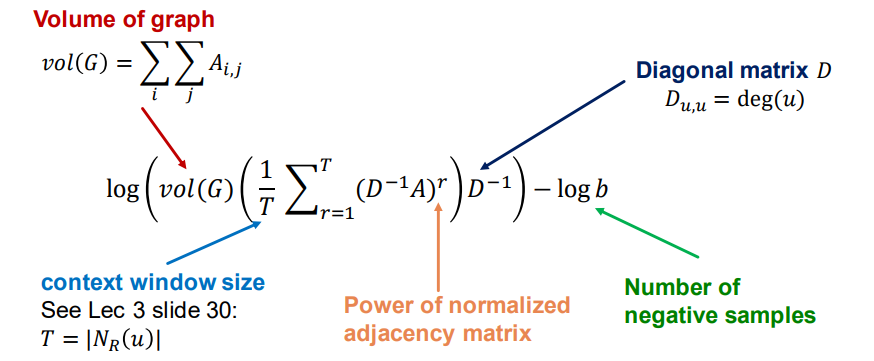
  • $vol(G)$ : 인접행렬 항목의 합 (#of edge의 2배?)
  • $D_{u,u}$ : 노드$u$의 차수를 나타내는 행렬(대각행렬)
  • $T$ : window size. 랜덤워크의 길이
  • $\log b$ : 네거티브샘플링한 수
  • $p_{uv} = w_{uv} / d_{uv} \rightarrow P=D^{-1}\cdot A$
  • Skip gram with negative sampling(SGNS)의 수식을 행 확률론적 행렬(Walk의 한걸음)의 거듭제곱으로 r개의 walk를 표현하여 유도

• 👇 논문에서 제시한 유도 과정

  

• 참고: DCST, Tsinghua

• 👇 node2vec 등등에 대한 행렬분해식

  

2.3. Limitations

• 랜덤워크의 행렬분해를 통해 노드를 임베딩하는 것의 한계점
  • (1) 동적그래프에 대한 문제
    • Training set에 없는 노드에 대한 임베딩을 계산할 수 없음
    • 네트워크의 모든 임베딩을 다시 계산하여야 한다는 한계점
    • 즉 동적 그래프에 대한 확장성이 부족
  • (2) 임베딩이 구조적 유사성을 포착할 수 없음
    • 구조적으로 유사한 부분그래프의 노드에 대한 임베딩이 매우 다르게 표현될 수 있음

      

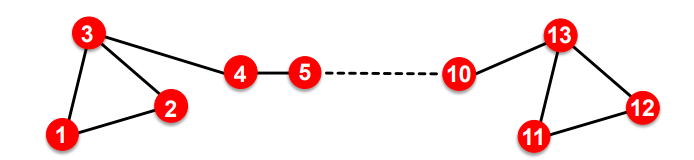
      • 노드 1과 노드 11은 구조적으로 유사(하나의 triangle 그래프의 구성요소이며, 차수는 2임)
      • 그러나 랜덤워크에서 노드1에서 시작하여, 노드11까지 도달할 수 있을까? $\rightarrow$ 아마 그렇지 않을 것이기 때문에, 매우 다른 임베딩을 갖게 될 것이라는 의미

    • 지역적으로 유사한 네트워크는 유사하게 임베딩되지만, 글로벌하게 구조적인 유사성을 포착할 수는 없음
    • AW(Anonymous walk)를 통해서 구조적인 유사성을 포착할 수는 있음
  • (3) node, edge, graph feature를 사용하지 않음
    • 가령 단백질 노드가 가진 속성 feature (임베딩에 도움이 될 수 있는 정보)가 있어도, 이를 활용하지 않고 구조적 연결관계만 사용
    • solution : 심층 표현 학습, GNN

참고

(1) J. Qiu, Y. Dong, H. Ma, J. Li, and K. Wang, "Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec," Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, ACM, 2018.