CS224W 6.1 Graph Neural Network

1. Introduction

1.1. Recap : Node embeddings

Lecture 3에서 노드임베딩에서 다루었던 내용에 대한 간략한 remind

• 노드임베딩의 Intuition

  • Input graph가 주어졌을 때, 각각의 노드들을 $d$-차원의 임베딩으로 매핑
  • 이 때, 그래프에서 유사한 노들이 가깝게 임베딩되도록 매핑하는 함수 $f(G)$를 학습!
    • Encoder-Decoder Framework에서의 목표 : $similarity(u,v) \approx \mathbf{z}_v^T\mathbf{z}_u$
    • Encoder : $ENC(v)=\mathbf{z}_v$
    • Similarity function : original network에서 $u, v$의 유사도
    • Decoder : Similarity function to 노드임베딩
  • Shallow Encoding approach : 모든 노드의 임베딩을 직접 학습하여 추론해냄

• Shallow Encoders의 한계

  • $O(|V|)$의 복잡도
    • 모든 노드에 대해 $d$차원의 임베딩을 구해야 하기 때문에
    • 학습해야하는 파라미터의 수가 그래프 노드의 수인 $|V|$에 비례
    • 노드 간 파라미터 공유 없이, 각각 계산해야함
  • transductive
    • 입력된 노드에 대해서만 임베딩가능하며, 동적그래프에 대해 적용 불가
  • node feature를 사용하지 않음
    • 많은 그래프들은 feature등의 속성을 가지고 있으나 이를 활용하지 않음

2. Deep Graph Encoders

2.1. Idea

• graph neural networks(GNNs) 기반의 deep method

  $ENC(v) =$ 그래프 구조 기반의 multiple layers 비선형 변환을 통해 최종임베딩 찾기

• deep encoders에 대한 참고사항 : lecture 3의 노드 유사도 function과 결합될 수 있음
• 즉, 유사성 함수를 인코딩하는 "Deep Encoder"에 대해 알아보자

2.2. Intuition

• Input : Graph
• Approach
  • (i) 네트워크의 비선형 변환의 여러계층을 통과
    • e.g. GC layer, Activation, Regularization, GC layer, ...
  • (ii) 최종적으로 노드 임베딩을 얻고, (sub)graph에 대한 임베딩을 얻음

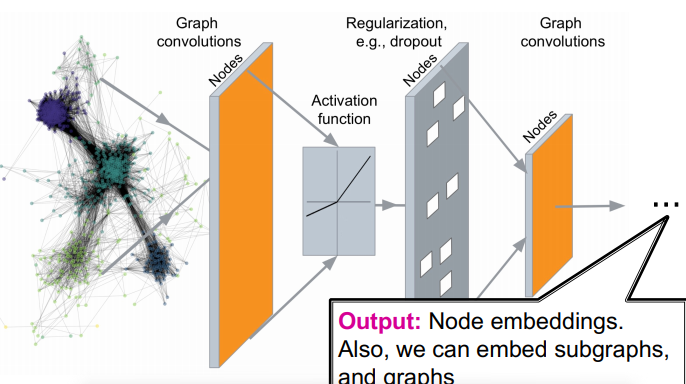
• Benefits : end-to-end 방식으로 training 가능

2.3. Tasks on Networks

응용 분야에 대해 살펴보기

• Node classification : 주어진 노드의 타입을 예측
• link prediction : 두 노드가 연결되었는가?
• community detection : 밀집 링크로 구성된 군집을 찾아내기
• network similarity : 두 네트워크가 얼마나 유사한가?

2.4. Modern ML Toolbox

그래프가 아닌, Image에서의 ML과의 차이점?

2.4.1. 기존의 데이터

• 기존 ML Toolbox는 심플한 형태의 데이터(단순시퀀스, 그리드)를 처리할 수 있도록 설계
  • Image data의 사례 : 고정된 크기의 행렬을 처리
  • Text/Speech : 선형 시퀀스를 처리
• Question : 더 복잡한 데이터 유형(그래프)을 어떻게 다뤄야하는가?

2.4.2. Networks의 난점

• 임의적인 크기(arbitrary size)
• 토폴로지 구조의 복잡성 (그리드와 같은 공간적 지역성이 없음)
• 노드의 ordering이 없음(기준점이라는 개념, 방향이라는 개념이 없음)
• 노드나 에지가 삽입되는 동적그래프이며, multimodal feature를 가지는 특성