CS224W 6.2 Basics of Deep Learning

1. Machine learning as optimization

1.1. Idea

• Supervised learning : $x$가 주어지면, label(or class) $y$를 예측하는게 목표
• Input $x$는?
  • 실수로 구성된 벡터
  • 시퀀스 데이터 : 자연어 시퀀스, 토큰 시퀀스, 음성 시퀀스
  • 행렬 : 동일한 크기로 크기가 조정된 이미지
  • 그래프 : 노드,에지 feature를 가지는 그래프
    이러한 x들을 y에 매핑하는 방식에 대해 학습해야할 것
• input $x$를 $y$에 매핑하는 함수의 학습을 최적화하는 문제를 다룸

1.2. 수식적 표현

• 1.1에서 제시한 최적화 문제를 아래와 같이 수식화할 수 있음

  $\displaystyle\min_{\Theta} \mathcal{L}(y,f(x))$
  예측된 값과 실제 값 사이의 불일치를 표현하는 것이 Loss

  • $\Theta$ : 최적화할 파라미터집합
    • 스칼라, 벡터, 행렬, 행렬집합 등이 될 수 있음
    • deepwalk에서의 사례를 생각하면, $\Theta=\{Z\}$, $Z$=임베딩룩업
  • $\mathcal{L}$ : loss function (예시:L2 loss,회귀분석에 자주 사용)
    • $\mathcal{L}(y,f(x))=||y-f(x)||_2$
      실제값-예측값의 차이의 제곱의 합
    • 일반적인 다른 loss function : L1 loss, huber loss, max margin, cross entropy..

1.3. Loss function example

• Cross entropy (CE)
  Loss func. CE에 대해 예제를 통해 개념을 알아보기
  • Label $y$를 categorical vector(one-hot encoding)으로 정의하면,
    • 예) $y = \{0, 0, 1, 0, 0\}$ $\rightarrow$ $y$는 class 3을 나타냄
  • 색상에 대한 확률분포를 모델링
    • $f(x) = Softmax(g(x))$
    • 예) $f(x) = \{0.1, 0.3, 0.4, 0.1, 0.1\}$
  • 녹색이 될 것으로 예상되는 확률과, 실제 녹색이 될 항목 사이의 loss 계산
    • $CE(y,f(x))=-\sum_{i=1}^{C}(y_i logf(x)_i)$
    • 모든 클래스 $C$에 대해 합산, $y_i$는 실제 label, $f(x)_i$는 예측값
    • 예측이 one-hot에 가까울수록, loss는 더 작아짐 ($log1=0, CE=0$)
  • 모든 훈련 예제에 대한 Total loss :
    - $\mathcal{L}=\sum_{(x,y)\in\mathcal{T}} CE(y,f(x))$
    • $\mathcal{T}$ : 모든$(x,y)$를 포함하는 트레이닝데이터, $x$:인풋,$y$:레이블

1.4. 목적함수(Loss)의 최적화 : 경사하강법

1.3까지를 통해 Loss function을 알아보았으며, 이를 어떻게 최적화할까?

1.4.1. 경사하강법의 기본 아이디어

• Gradient vector : 증가의 방향과 속도를 나타냄

  $\triangledown_{\theta}\mathcal{L}=(\displaystyle\frac{\partial\mathcal{L}}{\partial\Theta_1},\displaystyle\frac{\partial\mathcal{L}}{\partial\Theta_2},\ldots)$

• directional derivative
  • 주어진 지점에서의 해당 벡터에서 함수의 순간 변화율
• 다음의 문제를 해결
  • 손실이 가장 많이 줄어들도록 매개변수를 어느 방향으로 변경해야할까?
• 직관적 방법
  • 손실이 가장 빠르게 감소하는 방향으로 이동
  • 괜찮은 로컬 솔루션, 혹은 글로벌 최소 솔루션에 도달할 수 있기를 원함
  • 감소에 대해서만 관심이 있으므로, 기울기의 반대방향으로 이동 (-) 부호를 취함

1.4.2. 경사하강법 알고리즘

• Iterative algorithm
  • 그래디언트의 반대방향으로 $\Theta$가 수렴할때까지 업데이트를 반복
  • $\Theta\leftarrow\Theta-\eta\displaystyle\frac{\partial\mathcal{L}}{\partial\Theta}$
    • 파라미터가 있을때, 손실함수의 미분값을 계산하여,
    • 반대방향으로 웨이트를 업데이트
• Learning rate (LR) $\eta$
  • Gradient step의 크기를 결정하는 하이퍼파라미터
  • 처음에는 큰 단계를 밟고, 최소값에 가까워질수록 작아지게 (how?)
• 종료조건 : (ideal) 0 gradient
  • 실사용시엔, validation set의 performance가 증가하지 않을 때 중단

1.4.3. 확률적 경사하강법 (SGD)

• 일반적인 경사하강법 알고리즘의 문제점
  • 정확한 경사계산을 위해, 전체 데이터셋의 전달이 필요
    • $\triangledown_{\theta}\mathcal{L}(y,f(x))$ 에서, $x$는 전체 데이터셋
    • 수십억개의 데이터를 포함하는 현대의 데이터셋
    • 매 스텝마다 전체 데이터셋으로 연산하는것 : 너무 큰 연산
• 솔루션 : Stochastic gradient descent(SGD)
  • 모든 트레이닝 데이터셋에 대해 손실을 계산하는 대신
  • 매 스텝마다, 각기 다른 minibatch $B$를 선정하여 돌림
• SGD의 컨셉
  • Batch size : 미니배치에 포함될 데이터의 개수
  • Iteration : 미니배치를 이용한 SGD의 1 step
  • Epoch : 데이터 세트에 대한 전체 전달
    • 백만개의 데이터$\rightarrow$ 크기가 10인 100,000개의 배치
    • #iterations=#dataset size / #batch size
• SGD는 전체 기울기의 편향(unbiased)없는 추정치 계산 가능
  • 수렴률에 대해 보장하지는 않음
  • 수렴을 위해, 실사용에서는 learning rate에 대한 튜닝이 필요할 것
• SGD를 개선한 일반적인 optimizer :
  • Adam, Adagard, Adadelta, RMSprop ...

👉 개선된 Optimizer에 대한 참고사항

2. Neural Network Function

2.1. 1-linear layer case

f(x)의 간단한 사례에 대해서 알아보자!

• Objective : $\displaystyle\min_{\Theta} \mathcal{L}(y,f(x))$
  • 실제 딥러닝에서는, $f$는 매우 복잡한 구조로 되어있음
  • 심플하게 시작하기 위해 하나의 선형레이어로 정의할 수 있음
    • $f(x)=W\cdot x$라 정의하면, $\Theta=\{W\}$
  • $f$가 scalar값을 반환한다면, $W$는 vector
    • $\triangledown_{W}\mathcal{f}=(\displaystyle\frac{\partial f}{\partial w_1},\displaystyle\frac{\partial\mathcal{f}}{\partial w_2},\ldots)$
  • $f$가 벡터를 반환한다면, $W$는 weight matrix
    • $\triangledown_{W}\mathcal{f}=W^T$
    • $f$의 Jacobian Matrix

2.2. multi-layers case (Back-propagation)

2.2.1. 역전파의 개념

• Objective : $\displaystyle\min_{\Theta} \mathcal{L}(y,f(x))$
  • 보다 복잡한 레이어를 가정해보자
    • $f(x)=W_2 (W_1 x)$라 정의하면, $\Theta=\{W_1, W_2\}$
      • $h(x) = W_1 \mathbf{x}$, $g(z) = W_2 \mathbf{z}$
  • 💡 Chain rule :
    • $\displaystyle\frac{dz}{dx} = \frac{dz}{dy}\cdot\frac{dy}{dx}$
    • e.g. $\triangledown_x f = \displaystyle \frac{\partial f}{\partial (W_1 x)} \cdot \frac{\partial (W_1 x)}{\partial x}$
  • Back-propagation(역전파)
    기계적인 기울기 계산이 가능하게 한 방법이라는 점에서 유의미
    • chain-rule을 사용하여, 중간단계 기울기를 전파하고
    • 최종적으로 $\mathcal{L}$의 gradient(기울기)를 계산하는방식

2.2.2. 역전파 예제 (2-linear layers)

• 2-layer linear network 예제

  

  • $f(x)=g(h(x))=W_2 (W_1 x)$
  • $\mathcal{L} = \sum_{(x,y)\in\mathbf{B}}||(y,-f(x))||_2$
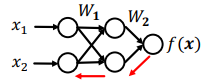
    • minibatch $\mathbf{B}$에 대한 L2 loss summation
  • Hidden layer : input $x$에 대한 중간단계 표현
    • $h(x)=W_1 x$를 hidden layer로 칭함 (중간단계 결과값)
    • $f(x) = W_2 h(x)$

• forward propagation

  • input으로부터 loss를 순차적으로 계산한다면,
    • $x \rightarrow(\times W_1) h \rightarrow (\times W_2)g \rightarrow \mathcal{L}$

• Back-propagation

  • $\displaystyle\frac{\partial\mathcal{L}}{\partial W_2} = \frac{\partial\mathcal{L}}{\partial f}\cdot\frac{\partial f}{\partial W_2}$
  • 두 번째 단계는 아래와 같이 첫단계의 결과를 이용할 수 있음
  • $\displaystyle\frac{\partial\mathcal{L}}{\partial W_1} = \frac{\partial\mathcal{L}}{\partial f}\cdot\frac{\partial f}{\partial W_2}\cdot\frac{\partial W_2}{\partial W_1}$

2.3. Non-linearity

활성화 함수에 대해 알아보자

• $f(x)$에서, $W$가 아무리 많아져도 계속 선형성이 유지됨
• 모델에 비선형성을 도입하면, 표현력이 증가함
• 비선형 함수의 예
  • $ReLU(x)=max(x,0)$
  • $\sigma(x) =\displaystyle\frac{1}{1+e^{-x}}$

2.4. Multi-layer Perceptron (MLP)

각 층에서 선형변환, 비선형변환을 결합하는 형태

• MLP의 수식을 살펴보면,

  $x^{(l+1)} =\sigma(W_l x^{(l)} + b^l)$

  • $W_1$은 $l$에서 layer $l+1$로 변환해주는 hidden representation
  • $b^l$은 layer $l$에서, $x$에 대한 선형이동 ($y=ax+b$)
  • $\sigma$는 non-linearity function (예:sigmoid)

3. Summary

• Objective function
  • Loss를 최소화하는 것을 목표로 하는 목적함수

    $\displaystyle\min_{\Theta} \mathcal{L}(y,f(x))$

    • $f$는 선형레이어, MLP, GNN 등이 될 수 있음

• input $x$에 대한 minibatch를 샘플링
• Forward propagation : input $x$에 대한 $\mathcal{L}$을 계산
• Back-propagation
  • $\triangledown_{\Theta} \mathcal{L}$ 을 얻기 위해, chain rule 적용
• SGD : 계산한 기울기를 이용하여, 여러 반복에 걸쳐 $\Theta$를 최적화

~끝~