1. Contents
6.3에서 전반적으로 다룰 내용
- Local network neighborhoods
- 집계 전략 설명 (aggregation strategies)
- computation graphs에 대한 정의
- Stacking multiple layers
신경망에 레이어 쌓기- 모델, 파라미터, 학습에 대한 설명
- 모델을 훈련하는 방법
- 감독/비감독 훈련에 대한 간단한 예시
2. Setup (표기법)
- Input Graph 를 다음으로 가정
- : vertex set (노드집합)
- : Adjacency matrix (binary로 가정, edge가 있으면1, 없으면0)
- : 노드 피쳐 행렬
- : 집합의 노드
- : 의 이웃노드 집합
- Node features
소셜 네트워크 : 프로필사진, 프로필내용
생물학적 네트워크 : 유전자 발현 프로필, 유전자 기능 정보- 노드 피쳐가 없는 그래프 데이터셋인 경우 아래 두가지 중 하나로 표현
- Indicator vectors로 노드를 표현 (one-hot encoding)
- Vector of constant 1: [1, 1, ... 1]
- 노드 피쳐가 없는 그래프 데이터셋인 경우 아래 두가지 중 하나로 표현
3. A Naive Approach (그래프 신경망)
3.1. Simple idea (naive)
- 그래프 인접행렬에 노드 피쳐를 join
- 이렇게 구성된 행렬을 심층신경망의 input으로 사용하는 방법

3.2. 문제점
- 너무 많은 파라미터의 수 :
- 다른 사이즈의 인풋 그래프에 대해 적용 불가
- Node 개수가 5개인 것과 7개인 것을 Input으로 넣는 케이스를 가정
- Hidden matrix의 사이즈가 계속 달라져야하는가..? 이는 학습 불가능
- 노드를 표현하는 순서에 따라 결과가 달라질 수 있음 (sensitive to node ordering)
- 그래프에는 고정된 노드 순서가 없기에, 그래프 노드를 정렬하는 방법이 불분명
4. Idea : Convolutional networks
이미지 처리를 하는 CNN의 직관을 그래프에 적용하여 일반화시켜보자
4.1 CNN on Image
- image를 학습하는 CNN 구조의 예시
- 슬라이딩 윈도우(e.g. 3by3 filter) 형태의 convolution 연산자 정의
- convolution subsampling 과정을 반복
- Goal 단순히 격자나 행렬간에 사용되는 컨볼루션의 개념을 일반화하여, 그래프에 적용
4.2. Problem : Real-World Graphs
- 그래프 데이터에 대해서는 '슬라이딩 윈도우' 개념을 적용하기 어려움
=지역성에 대한 어떤 고정된 표현 방법이 없음- 가령 행렬에 대한 10by10 슬라이딩 윈도우를 가정한다면?
- 어떤 케이스엔 노드3개 에지2개만 포함
- 또 다른 케이스엔 노드7개, 에지 12개를 포함할 수 있음
- 가령 행렬에 대한 10by10 슬라이딩 윈도우를 가정한다면?
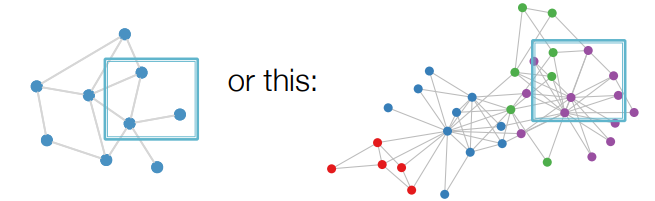
- 순열불변 속성을 가진다는 점
- 하나의 그래프에 대해 노드 혹은 에지가 나열된 순서를 바꿔도, 변하지 않음
- 즉 여러가지 표현형태를 가질 수 있다는 점
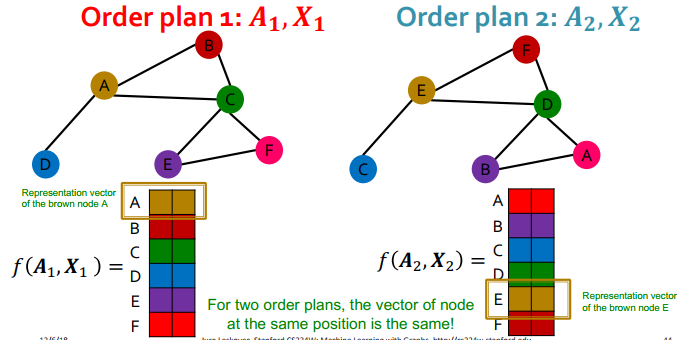
2023 강의에 추가된 부분
- 아래와 같이 다른 Order plan으로 정의된 동일한 그래프가 있을 때,
- graph 에 대하여
- 어떤 order plan 가 존재할 때, 를 만족
- 이를 만족시키는 를 순열불변함수(permutation invariant function)라 칭함
- 기존의 nn에 order가 다른 그래프 input을 넣으면, 결과가 다르게 나옴
4.3. Idea : from images to graphs
-
직관
- CNN의 단일 Convolutional layer를 생각해본다면 (3by3 filter 가정)
- Image : 3by3의 중심 픽셀이 주변 픽셀의 값을 집계 후, 새로운 픽셀생성
- Graph : 중심노드가 이웃노드의 값을 집계
- CNN의 단일 Convolutional layer를 생각해본다면 (3by3 filter 가정)
-
아이디어
위 직관을 통해 생각해낸!- 이웃 노드의 정보를 변환하고 결합하여 새로운 종류의 메시지를 생성
- 이웃으로부터의 메시지 를 변환 :
- 이를 집계 :
- 이웃 노드의 정보를 변환하고 결합하여 새로운 종류의 메시지를 생성
4.4. How works GCN
CNN의 직관을 통해 정리된 GCN의 아이디어를 알아보자
-
전반적인 아이디어
- 노드의 이웃이 신경망 아키텍처를 정의
- (i) 노드 계산 그래프(node computation graph)를 정의
- (ii) 계산그래프를 통해 정보를 전파하고 변환
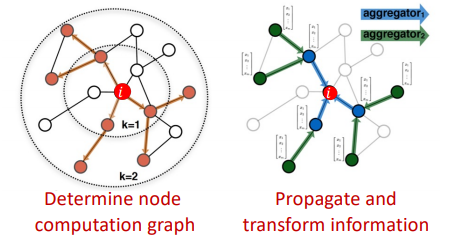
- 노드의 이웃이 신경망 아키텍처를 정의
-
아이디어 : Aggregate Neighbors
- target 노드 주변 지역의 로컬 이웃구조를 기반으로 노드 임베딩을 생성하자
- 직관적으로, 이웃구조가 비슷하다면 계산그래프도 유사할 것임 (이웃을이용하므로)
- 이웃노드로부터 전파된 메시지를 집계하는 과정을 각기 반복
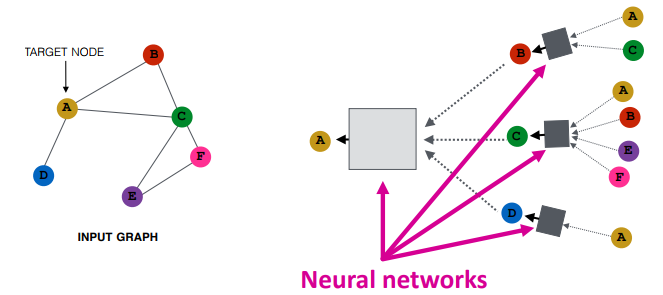
- 이웃노드로부터 전파된 메시지를 집계하는 과정을 각기 반복
- 기존신경망과의 차이점
- 모든 노드가 자체 신경망 아키텍처를 정의한다는 점
- 즉, 모든 노드는 주변 이웃 구조를 기반으로 자체 계산 그래프(computation graph)를 정의함
4.5. Deep Model : Many Layers
많은 레이어를 갖는 GCN의 모델의 깊이에 대한 논의
- 모델의 깊이는 임의적일 수 있음
- 노드들은 각 레이어마다 임베딩을 가지고 있음
- Layer-0에서 노드 의 임베딩은 이 노드의 input feature인 로 초기화
- 아래 그림에서 와 같은 표기 (input feature)
- Layer-k에서 임베딩은 hops만큼 떨어진 노드들의 정보를 가지고 있음
- 제한된 수 에 대해서만 수행함 (수렴의 개념이 없기 때문에, 수렴할때까지 반복X)
- 알려진 직경 정보가 없다면, 최대 100hop을 사용한다(?) -> 확인필요
- Layer-0에서 노드 의 임베딩은 이 노드의 input feature인 로 초기화
- 노드들은 각 레이어마다 임베딩을 가지고 있음
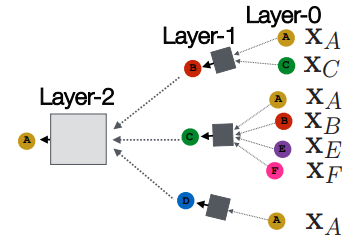
4.6. Neighborhood Aggregation
GCN 각 레이어에서, 이웃을 집계하는 function에 대해 정의해보자
-
Neighborhood Aggregation : 기존 NN과의 핵심적인 차이점이, 이 집계함수에 있음
- 집계 연산자는 순열불변이 되어야함
- 어떤 순서로든 노드를 배치할 수 있고, 이에 따라 노드를 집계하여도 항상 동일해야함
- e.g. 노드 B의 이웃 A,C, 집계연산자에 A,C가 들어오든 C,A가 들어오든 값동일
- 집계 연산자는 순열불변이 되어야함
-
각 layer의 Blackbox는 어떻게 처리할까? (hidden layer)
-
Basic approach : 이웃으로부터 정보들의 평균을 구하고, nn에 적용
- 참고 : 평균/합산 함수 = 순열불변함수 임!
-
Blackbox에서, 선형성+비선형성을 적용하여 다음 레벨 메시지를 생성 ()
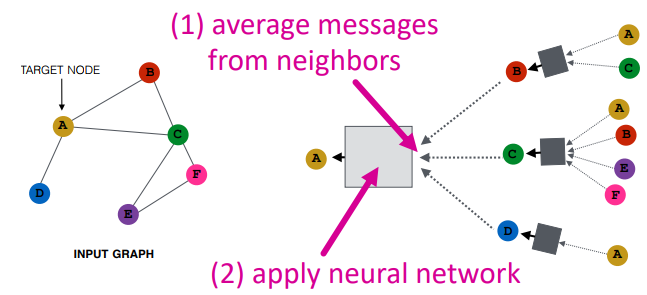
-
수식으로 어떻게 정의할까? (Deep Encoder)
h는 임베딩, 아래 첨자는 노드를 의미, 위 첨자는 신경망 layer의 수- :
0-th layer 임베딩은 노드피쳐와 동일함을 표현 - 수식(a)
- :
layer l에서의 노드v의 임베딩 - :
이웃노드들의 이전 레이어에서 임베딩된값들의 평균 - :
Non-linearity function (e.g. ReLu)(비선형성) - :
Total number of layers
-
L layer의 집계 이후의 임베딩
- :
-
4.7. Training the model
임베딩을 생성하기 위해 어떻게 모델을 훈련할까?
- 모델 훈련 방법을 정의하기 위해서는, 파라미터에 대한 정의 필요
4.7.1. Model Parameters
- 수식(a)에서, 와 이 학습가능한 weight matrix임
- 모든 레이어마다 다른 와 를 가짐
4.7.2. training을 위한 idea 및 중요점
- Idea : 임베딩을 손실함수에 입력하고, SGD를 수행해서 weight 파라미터들을 학습
- : 레이어 에서, 노드 에 대한 hidden representation
- : 이웃 집계를 위한 weight matrix
- : 자기 자신을 hidden vector로 변환하기 위한 weight matrix
- 중요점 : 가중치 행렬은 여러 노드에서 공유됨
- 모든 노드는 동일 Layer 에서 동일한 행렬 를 사용하여 변환함
4.8. Matrix Formulation
모델을 행렬변환하면, 행렬연산을 통해 효율적으로 수행할 수 있음
-
집계함수는 matrix operation을 통해 효율적으로 연산 가능
- : diagonal matrix,
- 대각성분에서만 degree값을 가지며, 그 외에 모두 0인 대각행렬
- : 대각성분에서만 1/degree값을 갖는 대각행렬 (의 역행렬)
- 위 정의에 따라,
- 이웃노드를 집계하는 것은, 대각행렬의 역행렬을 곱한것과 동치 (1/degree)
-
Matrix formulation에 의해, 수식(a)를 재정의해서 써보기
수식(b)
- 로 정의
- 실례에서, sparse matrix multiplication(희소행렬곱셈) 을 통해 효율적 수행 가능
💡희소행렬곱셈
- 0이 아닌 요소에 대해서만 연산을 수행
- 계산비용을 줄이고 메모리를 절약하는데에 도움이 됨
4.9. How to train a GNN
다시금 GNN을 training하는 법에 대해 다뤄봅시다..
-
: 인풋 그래프에 대한 노드임베딩
-
Supervised setting
- : 노드 레이블, 혹은 스칼라 값
- : L2 norm (=실수), cross entropy (=카테고리)
- 👇label 를 이미 가지고 있는 상황에서 직접 학습의 예 (drug-drug network 사례)
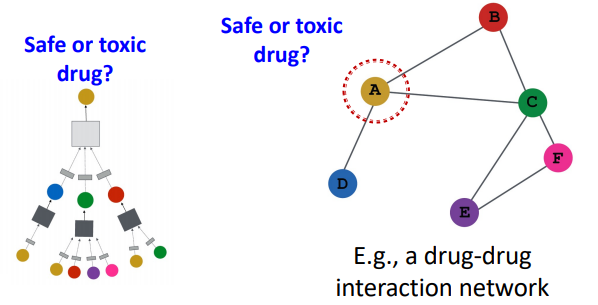
-
Unsupervised setting
- 사용가능한 노드레이블이 없는 경우
- 감독을 위해 그래프 구조를 사용할 수 있음
- 노드임베딩 챕터에서와 같이 내적과 네트워크 유사도를 근사하게 만들어서 학습하는 방법을 의미!! (deep encoder)
- 비감독 학습에 대한 예시
유사한 노드는 유사한 임베딩을 갖는다는 가정
- 노드 가 유사하다면,
- CE : 크로스엔트로피
- DEC : 내적 연산과 같은 디코더 (lecture 4)
4.9.1. Supervised training
- 노드 분류와 같이, supervised task를 위한 모델을 직접적으로 학습하는법
- cross entropy loss를 활용
- 이진분류에 대한 교차엔트로피 손실을 정의함
- (+) 후항은 noise, 앞쪽 항은 예측성공
- : 인코더 아웃풋 = 노드 임베딩
- : Classification weights, 최종분류에 대한 분류비율 (e.g. v로예측한 확률 0.6?)
- : 해당 노드의 클래스 레이블(독성이 있음=1, 없음=0)
- 모델을 돌리면, 를 만드는 matrix를 학습하게될것임 (Loss가줄도록)
- cross entropy loss를 활용
5. Overview🥵
- (1) neighborhood aggregation function에 대한 정의
- (2) 손실함수의 정의 (e.g. 크로스엔트로피 loss)
- (3) 학습 : 노드 집합에 대해 학습 진행
- 노드 배치를 선택하고, 계산그래프 생성하고 훈련을 진행
- (4) 모델 생성 이후, 필요에 따라 모든 노드에 대한 임베딩을 생성할 수 있음
- 훈련 데이터셋에 없는 노드에 대해서도 쉽게 임베딩을 생성할 수 있음
- = Inductive capability
- matrix가 모든 노드에 대해 공유되므로, 새로운 노드에 대해 적용가능
💡 는 노드의 피쳐수에만 의존하며, 그래프 크기에 의존하지 않기 때문에 - 따라서, unseen node에 대해 일반화되었다고 말할 수 있음
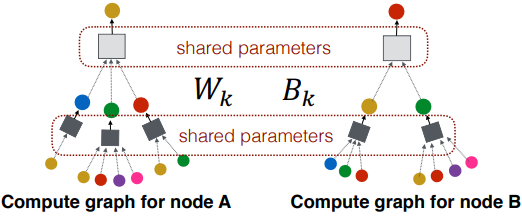
- matrix가 모든 노드에 대해 공유되므로, 새로운 노드에 대해 적용가능
- 간단한 응용의 예
- 동적 그래프에서 모델을 다시 학습할 필요가 없다는 점!
- 👇 새로운 노드가 등장하는 동적 그래프의 사례
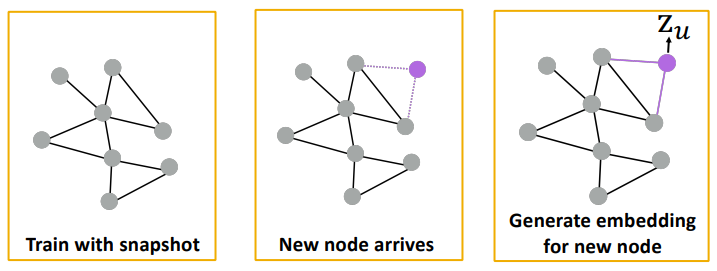
6. Summary
- 이웃 정보를 집계하여 노드 임베딩을 생성
- 앞으로 집계 프로세스가 수행되는 방식을 개선한 다양한 방식들에 대해 알아볼 것
- GraphSAGE architecture에 대해 Lecture 7에서 다뤄볼 것