❗ 문제 설명


❗ 제한사항

❗ 입출력 예

문제 요약
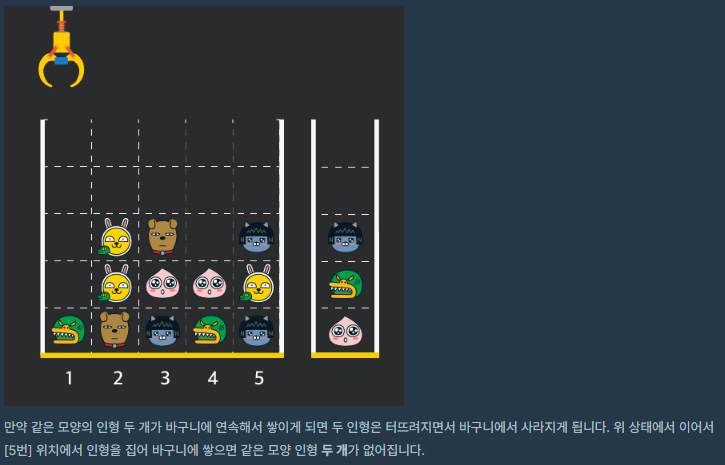
게임화면은 N x N 크기의 정사각 격자 형태이다.
크레인을 움직여서 인형을 집어올려 바구니에 쌓는다.
바구니에 같은 인형 2개가 연속으로 쌓이면 사라진다.
크레인을 모두 작동시킨 후 바구니에서 사라진 인형의 개수를 구하라.
문제를 보고 생각한 구현 방식
- 바구니는 스택형식으로 구현해야겠다.
-> Why?
바구니는 아래부터 차곡차곡 쌓이는 구조를 가지고 있기 때문에 그렇게 생각했다.
- 사라진 인형의 개수를 구하는 방식은 2가지라고 생각했다.
- 첫번째 방식은 일단 크레인을 다 작동시켜서 바구니에 가져와야할 인형을 다 담아놓고 없애는 방식
- 두번째 방식은 크레인을 작동시킬 때마다 바구니에 맨위에 있는 인형과 비교해서 같으면 바구니에 넣지않고 인형을 없애는 방식
나는 두번째 방식을 선택했다.
-> Why?
첫번째 방식은 크레인을 다 움직이고 인형을 없애야 하기 때문에 for문이 두 번 들어가야할 것 같다고 생각했다.
두번째 방식은 크레인을 움직이면서 인형을 없애기 때문에 for문을 한 번만 사용해서 구현할 수 있을 것 같다고 생각했다.
그래서 두번째 방식이 더 효율적이라고 생각해서 두번째 방식을 선택했다.
코드 1.
function solution(board, moves) {
let bucket = [];
let result = 0;
for(let i = 0; i < moves.length; i++) {
let pick = moves[i]-1;
for(let j = 0; j < board.length; j++) {
if(board[j][pick] === 0) {
continue;
} else {
if(bucket[bucket.length-1] === board[j][pick]) {
bucket.pop();
board[j][pick] = 0;
result += 2;
break;
} else {
bucket.push(board[j][pick]);
board[j][pick] = 0;
break;
}
}
}
}
return result;
}첫번째 코드도 통과를 하지만 테스트케이스 4번에서 다른 케이스에 비해 상당히 오래 걸리는 것을 볼 수 있다.
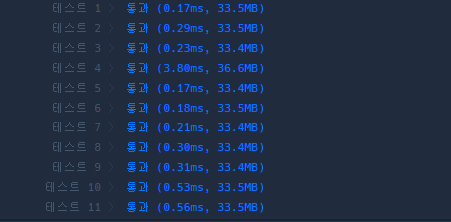
왜 그럴까 생각해봤더니 위 코드는 pick번째 열의 행을 모두 순회하면서 인형이 있는 칸을 찾아내는 방식이다. 즉, 인형이 없는 칸도 순회를 해서 값이 있는지를 확인하게 된다.
만약, board배열이 30x30이라면 크레인을 한 번 움직일 때마다 최악의 상황에는 반복문을 30번 진행하게 된다.
이 코드를 개선하기 위해 인형이 담긴 board배열도 0을 제외한 인형만 담긴 스택배열로 만들면 되겠다고 생각했다.
코드 2.
function solution(board, moves) {
const stack = new Array(board.length).fill(0).map(() => [])
const bucket = [];
let result = 0;
for(let i = 0; i < stack.length; i++) {
for(let j = board.length-1; j >= 0; j--) {
let doll = board[j][i];
if(doll !== 0) stack[i].push(doll);
}
}
for(let i = 0; i < moves.length; i++) {
let pick = moves[i]-1;
if(stack[pick].length !== 0) {
const pick_top_doll = stack[pick].pop();
if(bucket[bucket.length-1] === pick_top_doll) {
bucket.pop();
result += 2;
} else bucket.push(pick_top_doll);
} else {
continue;
}
}
return result;
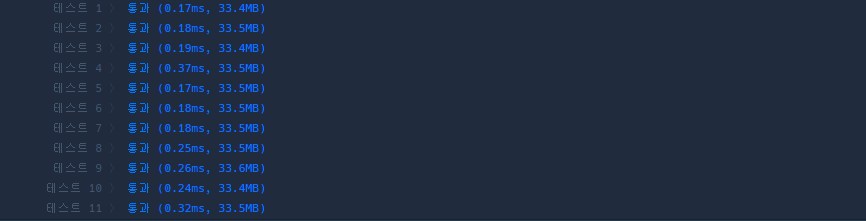
}두번째 코드로 검사를 진행해보면 테스트케이스 4번이 10배가 빨라진 것을 확인할 수 있다.
마무리하며
처음에 배열을 생각할 때 가로로된 배열을 위에서 아래로 쌓는 구조가 아닌 세로로된 배열을 왼쪽에서 오른쪽으로 쌓는 구조라고 생각하여 문제 이해를 잘못했다.
문제를 꼼꼼하게 읽는 연습을 좀 더 해야겠다는 생각이 들었다.

