이차형식에 대한 약간의 고찰

왜 우리는 이차형식에서 $x^TAx$ 에서 왜 A를 대칭행렬로 두고 계산을 하는 것일까?

• 그 이유는 직교 대각화가 가능 하기 때문이다.

증명

$D = P^TAP$
p가 직교 행렬이므로 아래와 같다
$A = PDP^T$

그리고 D는 대각행렬 이면서 대칭 행렬이기에
$A^T = (PDP^T)^T = PDP^T = A$

다시 정규분포로

• 중심 극한 정리에 따르면, 여러 개의 확률 변수들의 합에 해당하는 확률 변수는 몇몇 조건하에서 합해지는 확률 변수의 숫자가 증가함에 따라서 점점 가우시안 분포가 되어간다.

마할라비노스 거리

$y = U(x-\mu)$

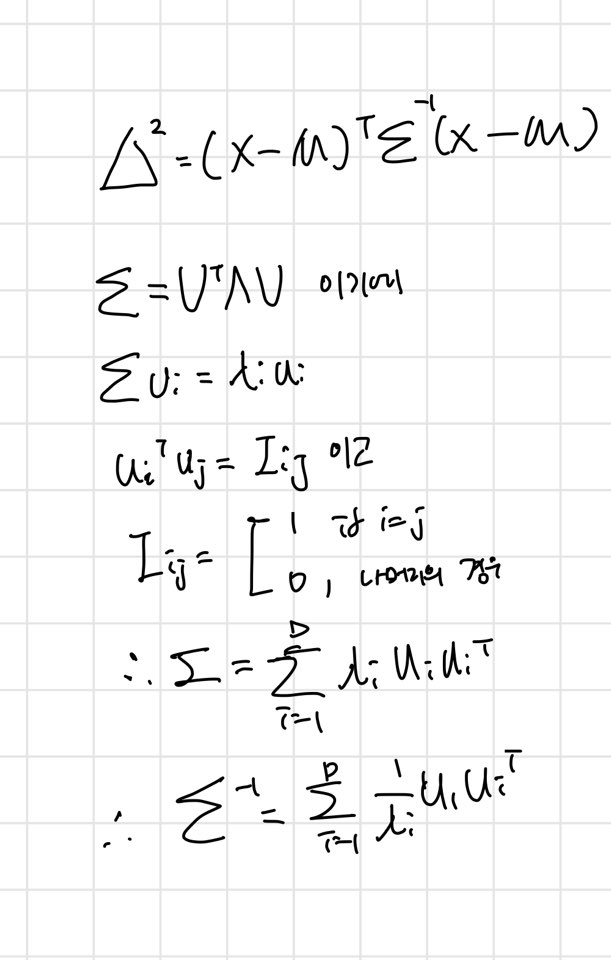
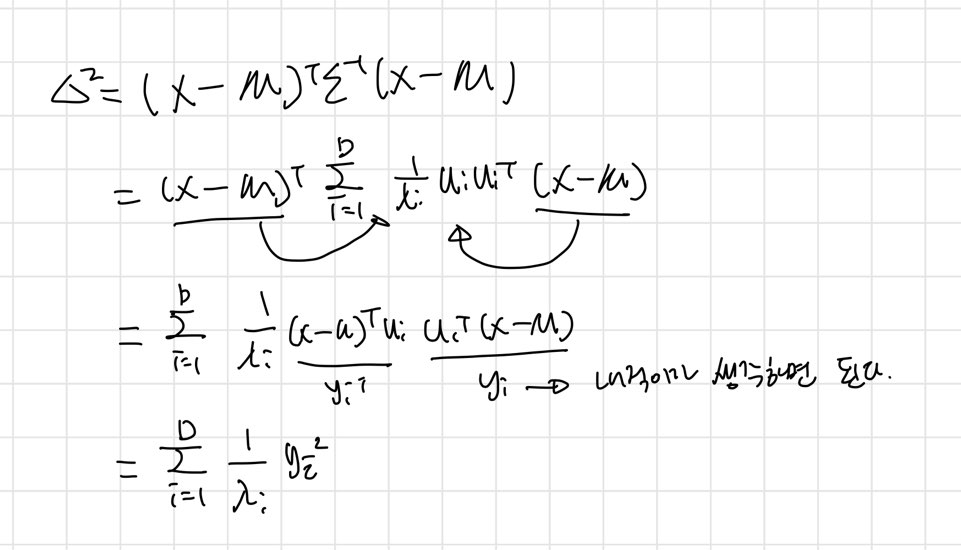
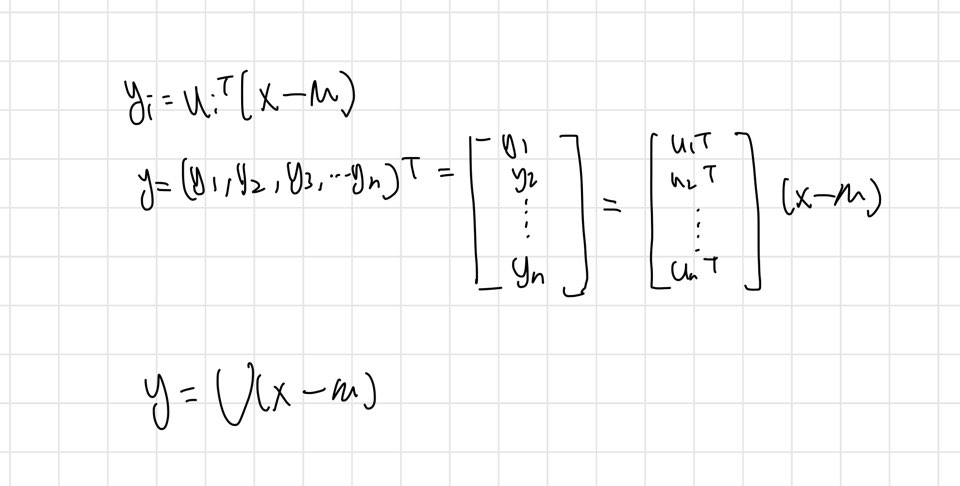
${y_i}$를 정규 직교 벡터 $u_i$들로 정의되는 새로운 좌표계라고 해석할 수 있다.

여기서 $U$는 각각의 행이 $u_i^T$로 주어지는 행렬이다. $U$가 직교하는 행렬임을 위에서 보았다.

x 좌표계에서 y 좌표계로 변환되는 과정에서 야코비안 J행렬을 가지게 되었다. J 각의 원소는
다음과 같이 주어진다.

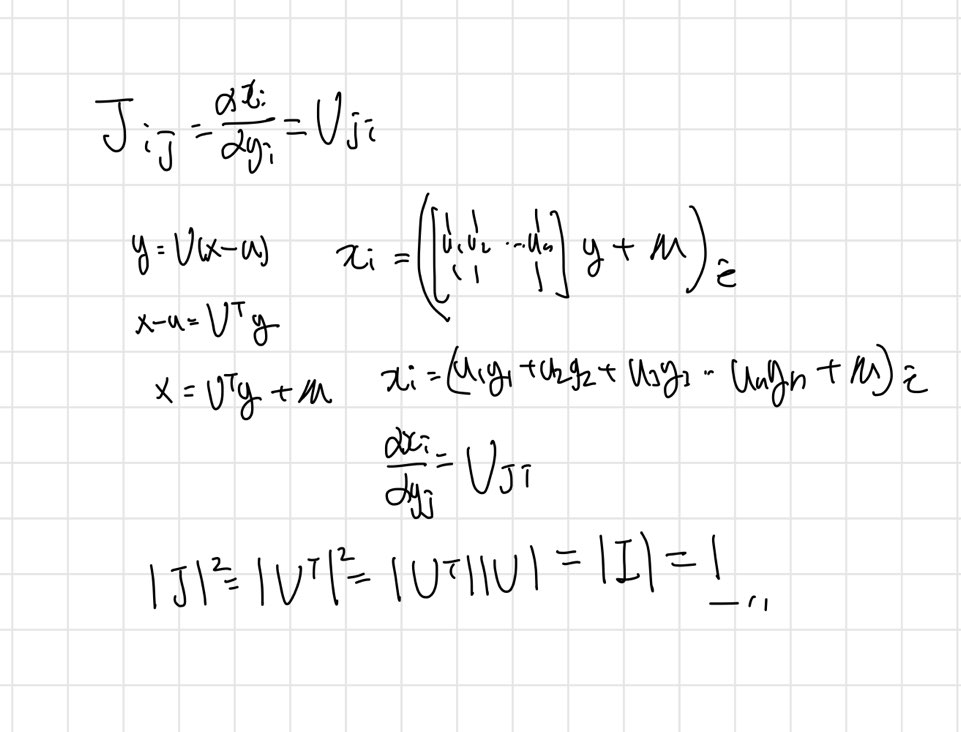
D개의 독립적인 단변량 가우시안 분포들의 곱에 해당한다. 이때 결합 확률 분포는 회전된 새롱누 좌표축에 따라 독립 분포들의 곱으로 인수분해된다. y좌표계상에서 분포의 적분은 다음과 같게된다.

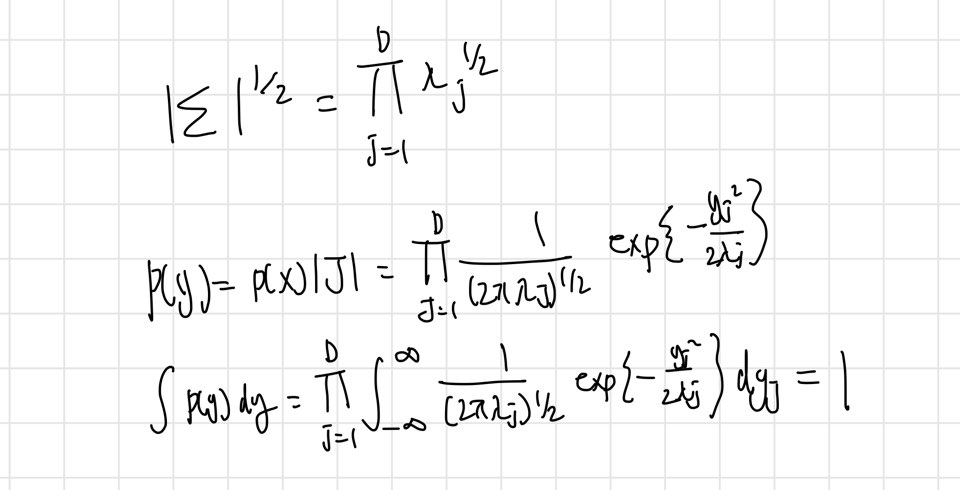
따라서 다변량 가우시안 분포는 정규화가 된 것을 증명했다

reference

크리스토퍼 비숍, 패턴 인식과 머신 러닝, 김형진, 제이펍 2018년 09월 10일, 87-91

Week 12 : Chapter 8 행렬의 대각화 part 2, SKKU Linear Algebra 선형대수학, 2020년 01월 11일 접속, http://matrix.skku.ac.kr/K-MOOC-LA/cla-week-12.html