스터디에서 진행한 DP 세미나 내용을 바탕으로 작성되었다.
코딩테스트에서 난이도있는 문제가 나온다면 단골로 출제되는 유형인 동적계획법(Dynamic Programming)에 대해 알아보고 DP문제가 나왔을때 어떻게 접근해야할 지 실제로 문제 풀이를 따라가며 알아보자.
또한 DP를 코딩테스트 통과에 그치지 않고 실문제 해결에 어떻게 활용할 수 있는지 사례를 통해 소개하고자 한다.
What is DP & Why DP? (DP는 무엇이고 왜 사용하는가?)
DP란 무엇인가?
Dynamic Programming(이하 DP), 한글로 동적계획법이라고 불리는 것의 사전적 정의는 아래와 같다.
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법
- Wikipedia
특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법
- NamuWiki
이를 정리하여 내가 정의하는 DP는 큰 문제를 반복되고 동일한 작은 문제로 나누어 해결하는 방법이다.
DP vs Divide and Conquer
이 내용을 보고 분할정복(Divide and Conquer)와 비슷하여 혼동할 수 있지만 둘은 분명한 차이점이 있다.
<분할정복>
그대로 해결할 수 없는 문제를 작은 문제로 분할하여 해결하는 방법이나 알고리즘
- Wikipedia
DP는 부분 문제들이 동일하다는 특징이 있고, 문제가 동일하다면 답도 동일하므로 이전에 계산한 답을 나중에 그대로 가져다 쓰면 된다.
이것이 추후 설명하게 될 Memoization이다.
반대로 분할정복은 부분 문제들이 동일하지 않고, 큰 문제 하나를 작은 규모의 여러 문제로 바꾸어 푸는 것이다.
다시 말하자면 DP는 Memoization을 이용하여 큰 문제를 반복되고 동일한 작은 문제로 나누어 해결하는 방법이다.
Memoization
Memoization은 Caching과 같은 의미로 이해하면 좋다.
동일한 계산을 반복해야 할 경우, 한번 계산한 결과를 저장해 두었다가 꺼내 쓰는 방식이고, 이는 공간 비용을 이용하여 시간 비용을 줄이는 효과를 얻는 것이다.
When to DP? (DP를 사용할 수 있는 조건)
Overlapping Subproblems
동일한 작은 문제가 반복되어 나타나는 경우로 대표적인 예는 fibonacci, binomial coefficient가 있다.
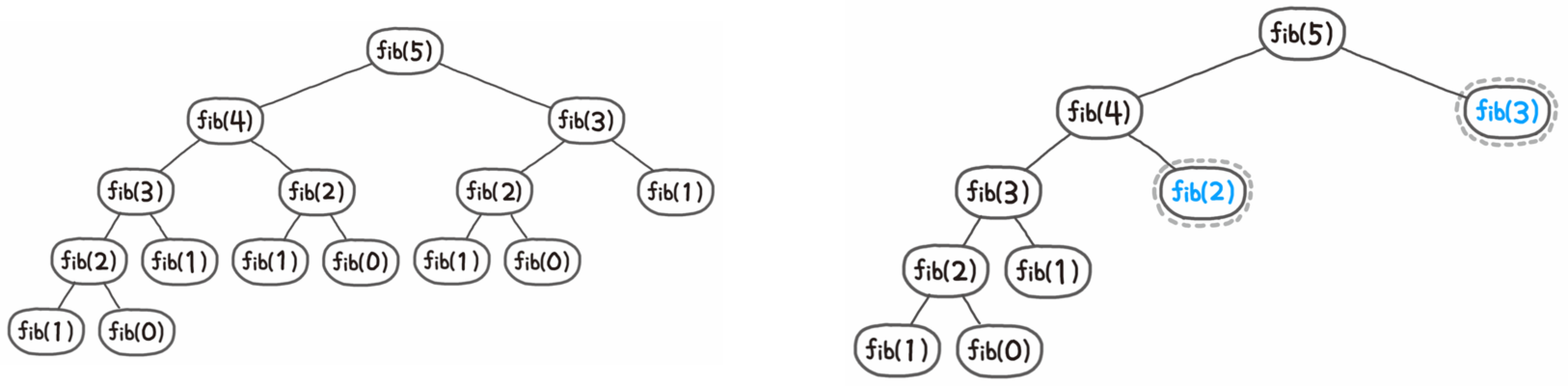
피보나치 수열의 5번째 수를 구하는 것을 보자.
왼쪽과 같이 fib함수가 재귀적으로 호출되는 것을 트리 형태로 나타낼 수 있는데, fib(2)와 fib(3)은 fib(4)의 왼쪽 자식 트리에서 이미 수행된 것을 확인할 수 있다.
DP에서는 이전에 계산한 문제의 답을 활용하기 때문에 오른쪽의 두 파란 노드에서 더이상 재귀함수가 호출되지 않아도 된다.
Optimal Substructure
부분 문제의 최적 결과 값을 이용하여 전체 문제의 최적 결과를 만들 수 있는 경우로 대표적인 예는 Floyd-Warshall, Bellman-Ford가 있다.
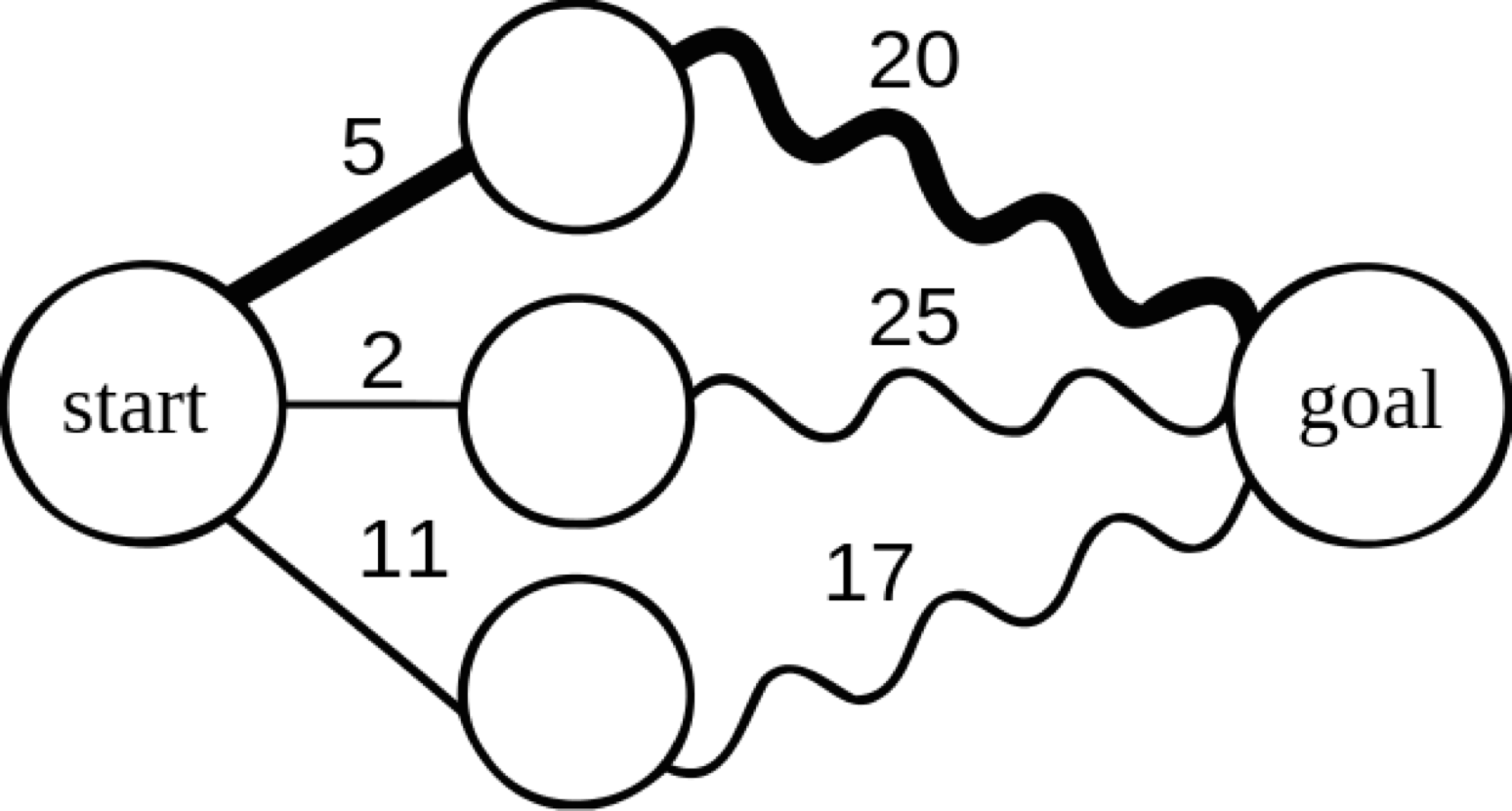
start에서 goal로 가는 최단 경로를 찾기 위해 중간 지점의 노드들 간의 최단 거리가 구해져있다고 하자.
start↔중간지점, 중간지점↔goal 사이의 거리는 모두 최단경로의 길이로, 부분 문제의 최적 결과 값이다.
전체 문제의 최적 결과 값인 start에서 goal로 가는 최단 경로는 (start↔중간지점)+(중간지점↔goal)값 중 최소값을 갖는 경로가 될 것이다.
How to DP? (DP를 이용한 Problem Solving)
⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️
이 내용은 순전히 개인적인 노하우로, DP 문제를 접근하는 한 가지 방법 정도로 참고만 하기 바란다.
DP 문제는 정말 많은 유형이 있고 고수준의 구현 능력 또한 요구하기 때문에 다양한 DP 문제를 풀어봐야 하고, 구현력을 키우기 위한 노력도 많이 기울여야 한다.
⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️
DP 문제를 푸는 것은 점화식을 만드는 것과 같다.
<점화식>
인접한 항들 간의 관계식
점화식을 만드는 것이 DP 문제를 푸는 것의 시작이자 끝이다.
매우 간단해 보이지만 정말 다양한 형태의 점화식이 등장하게 되고 이를 구상해내기 위해 많은 노하우와 수학적 고찰이 필요하다.
이제부터 피보나치 문제와 BOJ의 경찰차 문제 풀이를 따라가며 DP 문제를 어떻게 풀어가는지 알아보자.
경찰차 문제는 solved.ac에서 2023년 3월 기준 Platinum4 난이도로 책정돼있는 만큼 꽤 난이도있는 문제이다.
이 문제를 같이 풀어보면서 자신감을 얻어가길 바란다.
1단계 : 상태 결정
‘상태’란 점화식의 일반항을 말하며, 위에서 이야기한 ‘부분 문제’와도 같은 의미이다.
즉, DP 정의에서 나온 ‘동일한 부분 문제’로 나누는 것이 DP 문제를 푸는 첫 단계이다.
상태를 나눌 때는 index가 포함된 Subtask로 나누기 위해 노력하면 좋다.
무슨 말인지 모를 초심자들을 위해 팁을 준비했다.
💡 문제의 형태를
A일 때 B한 C값을 찾아라라고 바꾼 뒤,
A를 index로 잡고 생각해보자.
또한 문제에서 최종적으로 요구하는 C가 무엇인지 확인하자.
C는 최종 답안이며 이는 마지막 index의 Subtask 결과값을 의미한다.
피보나치 수열
피보나치 수열에서 19837번째 수를 구해보자.
이 문제는 n이 19837일 때 피보나치 수열에서 n번째 수를 찾아라라고 바꿀 수 있다.
위의 팁에 따라 19837이 index가 되고 상태는 n번째 수가 된다.
경찰차
경찰차 문제는 n번째 사건까지 처리했을 때 두 경찰차의 이동거리 합의 최솟값을 찾아라라고 바꿀 수 있다.
마찬가지로 위의 팁을 적용하면 입력 예시에서는 n이 3이므로 3이 index가 된다.
2단계 : 점화식 만들기
앞서 결정된 상태들 간의 관계를 찾아 점화식을 만들면 된다.
💡 문제의 형태가
A일 때 B한 C값을 찾아라일 때,
보통 B가 관계의 힌트가 된다.
또한 DP는 memoization이라고 했으므로, 특정 상태의 값을 결정할 때 이전 상태의 값을 어떻게 활용할 수 있는지 생각해보자.
피보나치 수열
n이 19837일 때 피보나치 수열에서 n번째 수를 찾아라라는 문제에서 B에 해당하는 ‘피보나치 수열’의 특징을 생각해보면 상태 간의 관계를 쉽게 찾아낼 수 있다.
경찰차
n번째 사건까지 처리했을 때 두 경찰차의 이동거리 (누적)합의 최솟값을 찾아라라는 문제에서 누적합이라는 점에 착안하여 아래와 같이 관계식을 나타내보자.(사실 이 접근은 잘못되었지만 왜인지는 추후 설명하겠다)
3단계 : 구현
DP를 구현하는 두 가지 방법
DP를 구현하는 두 가지 방법으로 Top-Down 방식과 Bottom-Up 방식이 있다.
각각을 이용해 피보나치 문제를 해결하는 파이썬 코드를 살펴보자.
- Top-Down
n = 5
D = [-1 for _ in range(n+3)]
def fibonacci(num):
if D[num] != -1:
return D[num]
if num <= 2:
D[num] = 1
return D[num]
D[num] = fibonacci(num-1) + fibonacci(num-2)
return D[num]
print(fibonacci(n))- Bottom-Up
n = 5
D = [-1 for _ in range(n+3)]
D[1] = 1
D[2] = 1
for i in range(3, n+1):
D[i] = D[i-1] + D[i-2]
print(D[n])이름 그대로 어느 일반항부터 계산할지에 따라 두 가지 방법으로 구현이 가능하다.
하지만 모든 DP 문제가 Top-Down과 Bottom-Up을 둘 다 사용할 수 있는 것은 아니며, 문제에 따라 둘의 효율이 달라지기도 한다.
따라서 DP 문제를 많이 풀어보면서 문제에 따라 어떤 구현방식이 좋을지 익혀야 한다.
경찰차
앞서 세운 점화식을 구현하기 위한 방법을 생각해보자.
위 점화식은 두 가지로 존재한다.
X1과 X2는 경찰차1,2가 각각 n-1번째 사건 처리 직후 어느 좌표에 있는지 알아야 계산이 가능하다.
이것이 가능한가?
경찰차1이 n-1번째 사건을 처리했다고 가정하자. 경찰차2가 마지막으로 처리한 사건은 몇 번째일까? 1~n-2까지 n-2개의 경우의 수가 가능하다.
경찰차2가 n-1번째 사건을 처리했다고 가정했을 때도 마찬가지이다.
풀이가 너무 복잡해지고 실제로 이는 시간복잡도 측면에서도 좋지 않다.(시간복잡도 : )
위 풀이는 Top-Down 방식으로 접근하다 보니 문제가 있음을 알 수 있었다.
따라서 Bottom-Up 방식은 어떨지 생각해보자.
앞서 두 경찰차가 마지막으로 처리한 사건이 몇 번째인지 알아두는 것이 중요하다는 것을 느꼈을 것이다.
따라서 상태를 다시 정의할 필요가 있다.
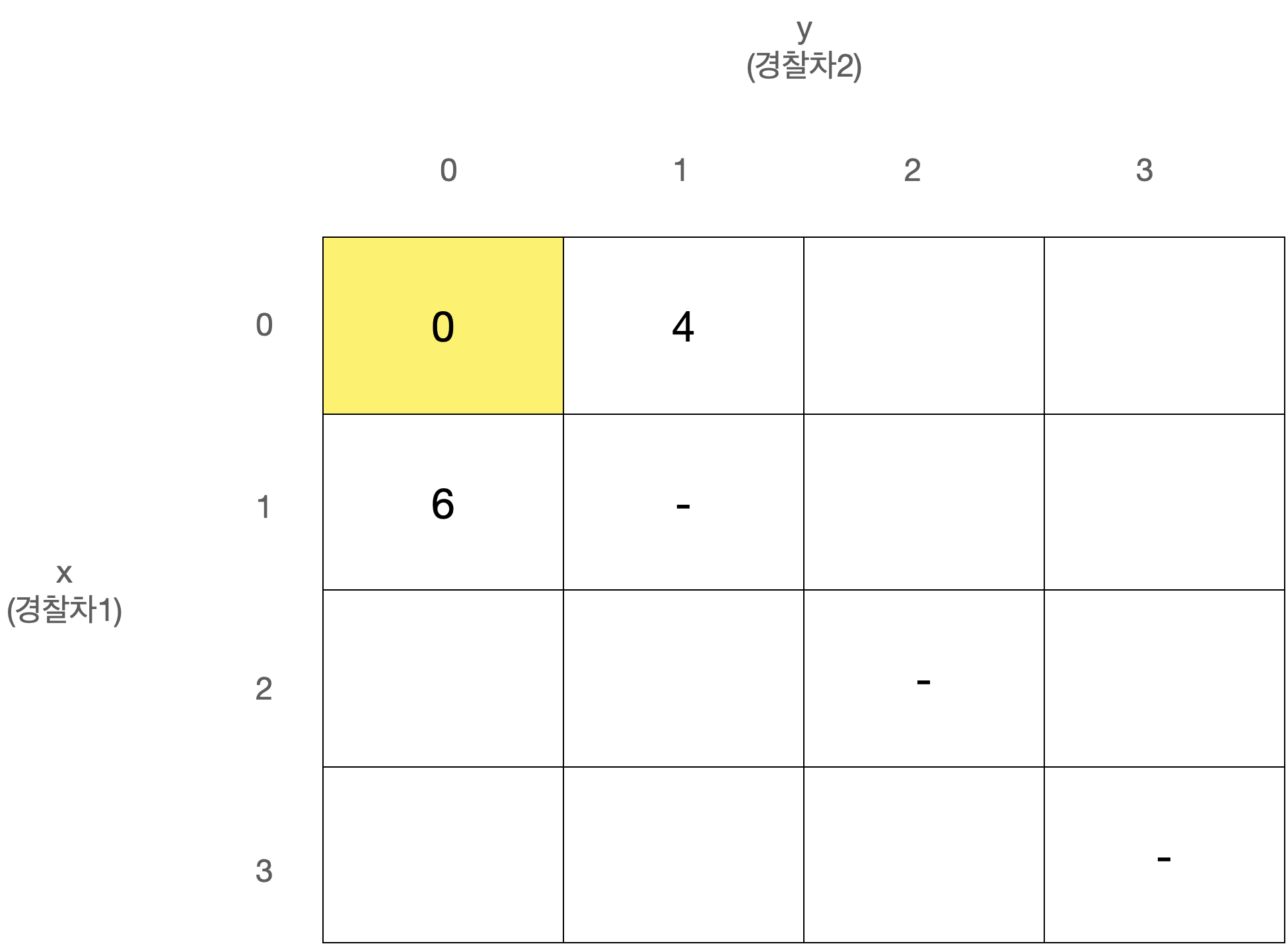
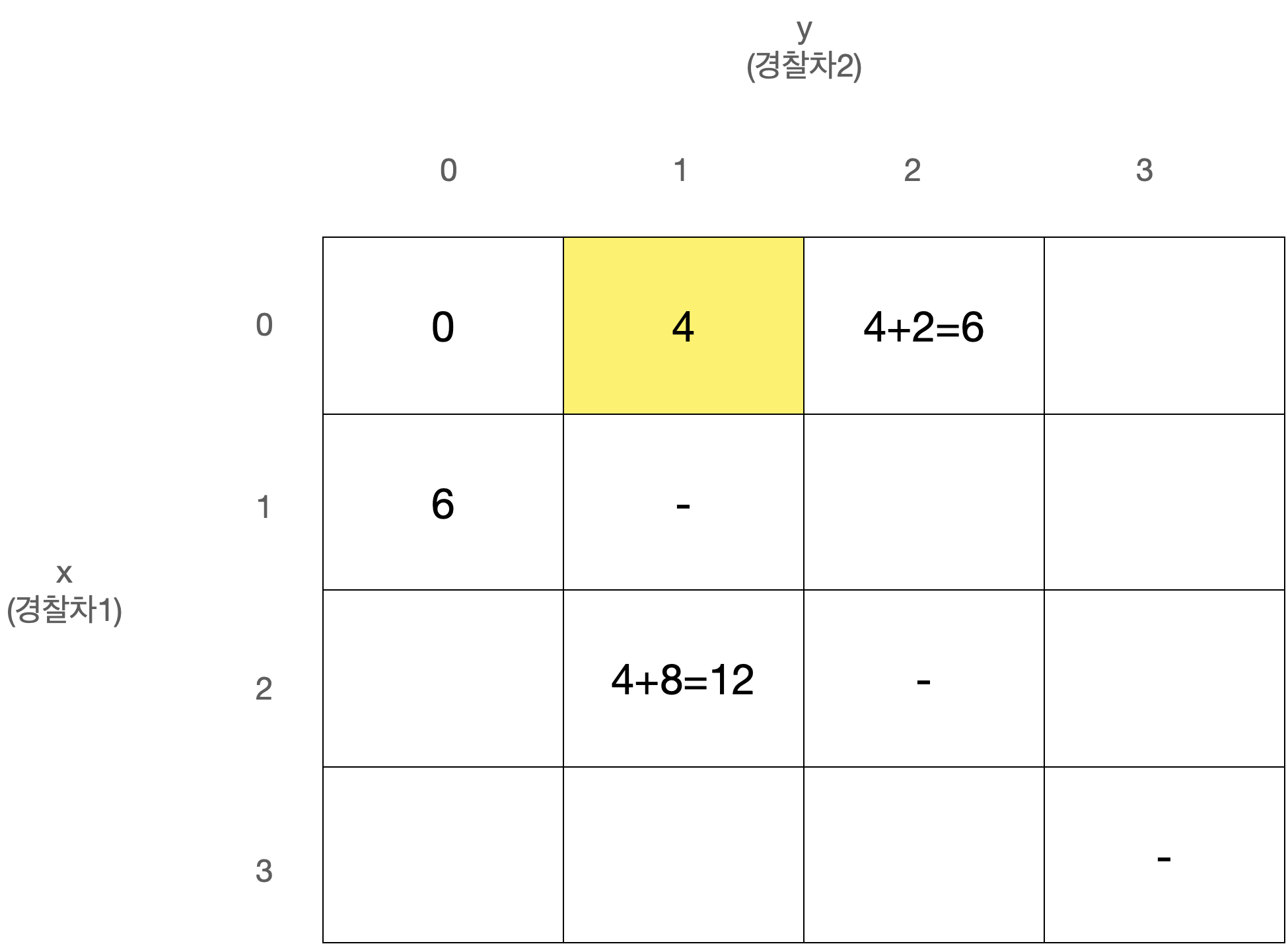
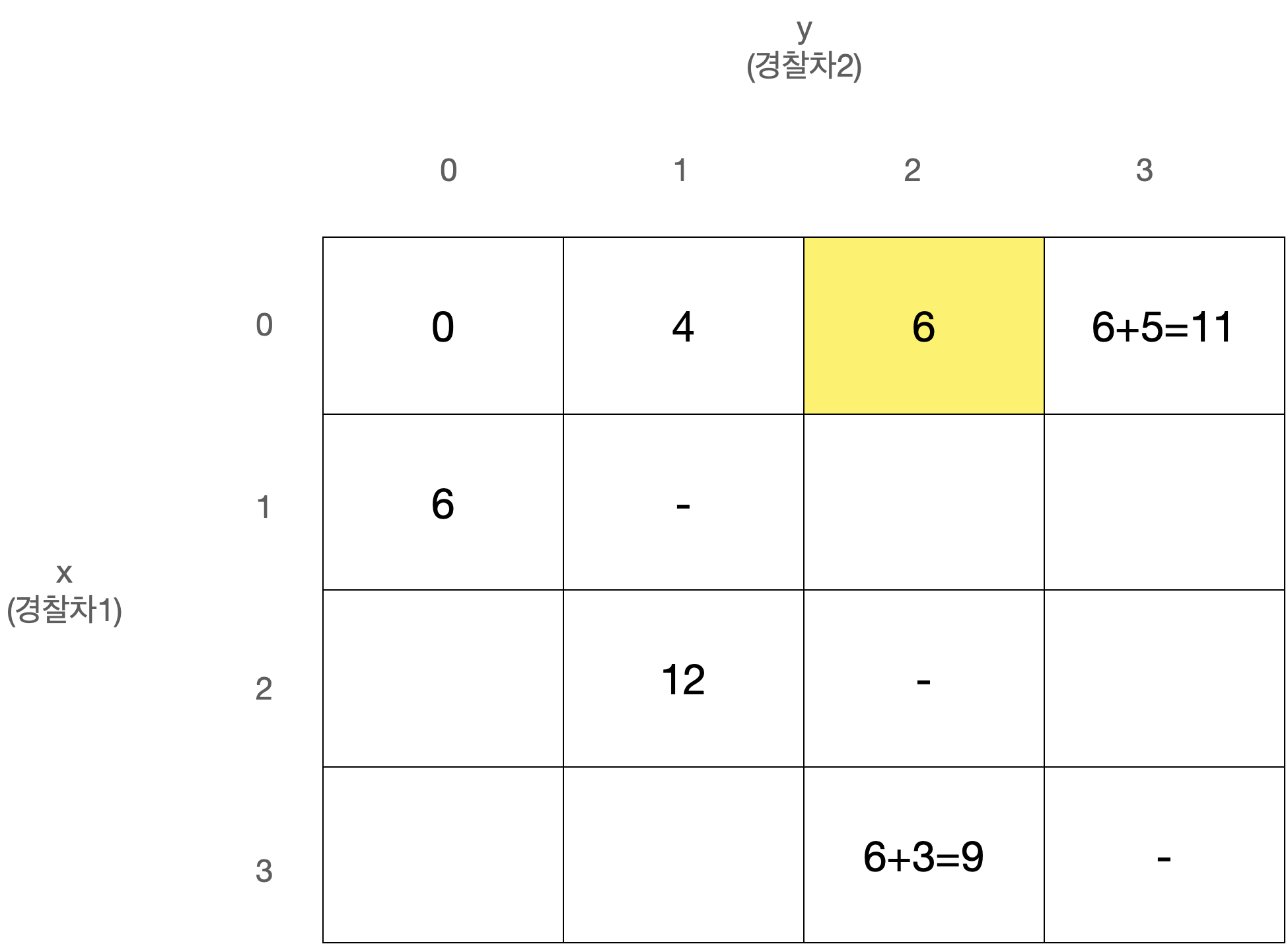
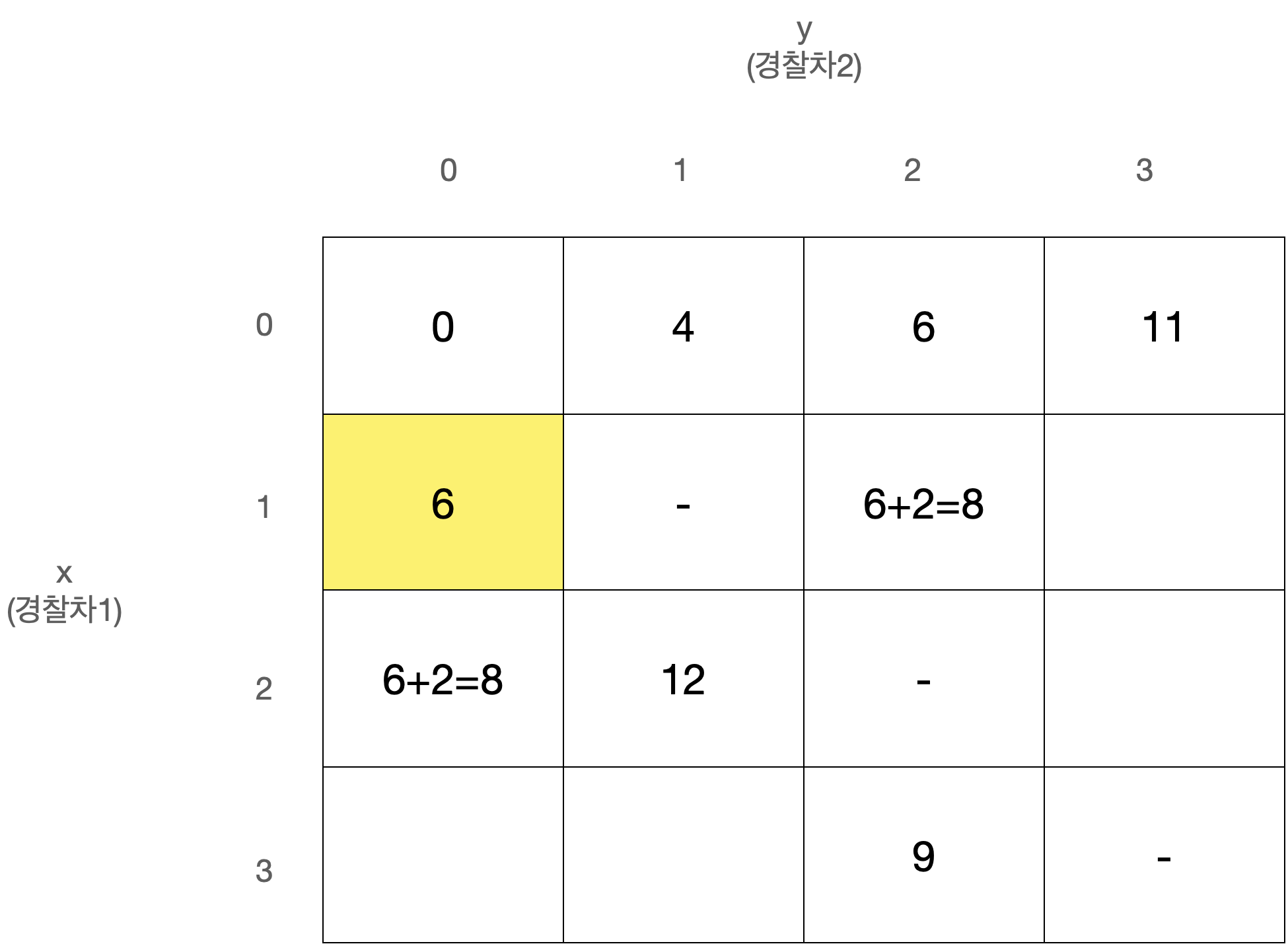
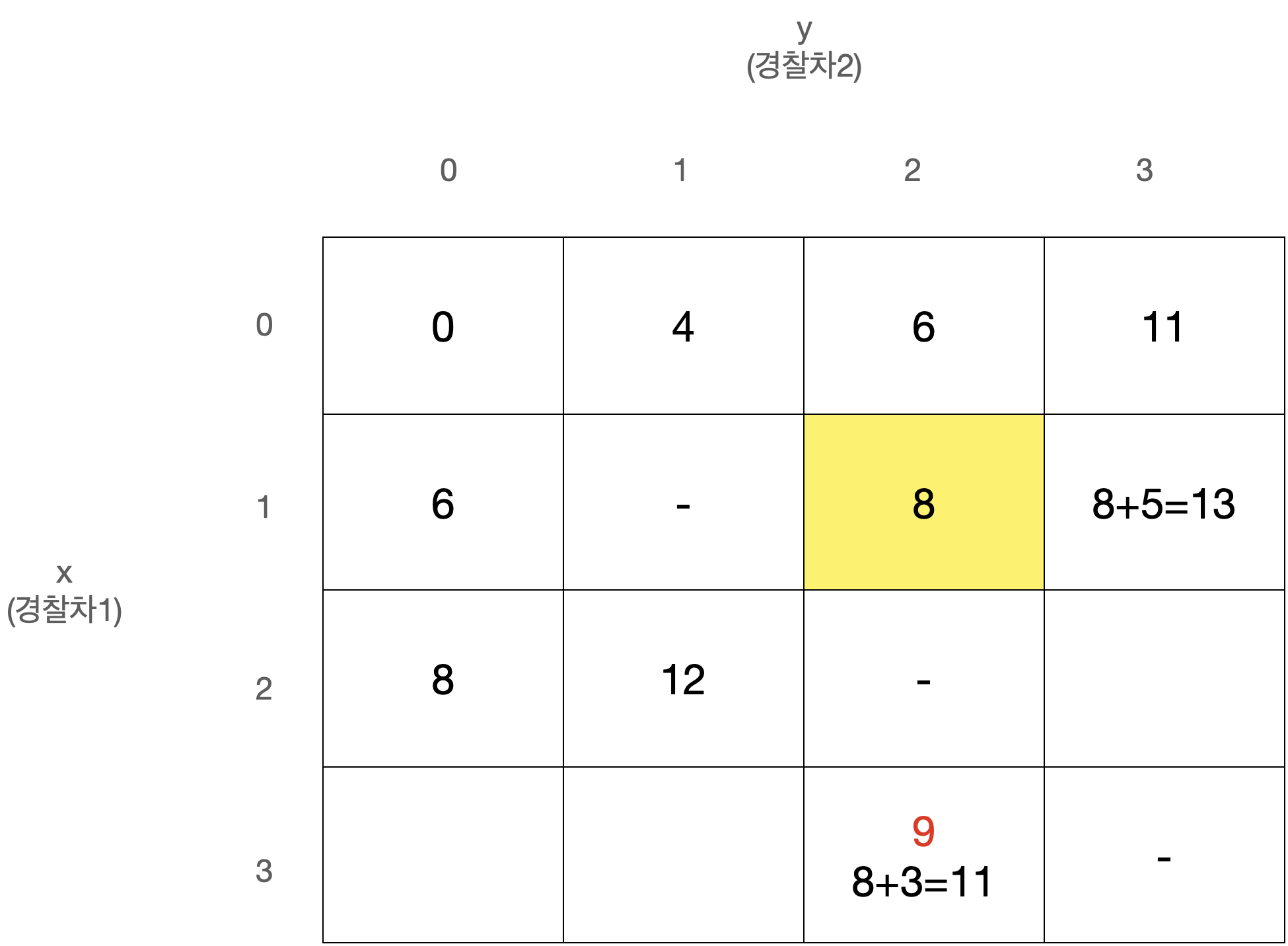
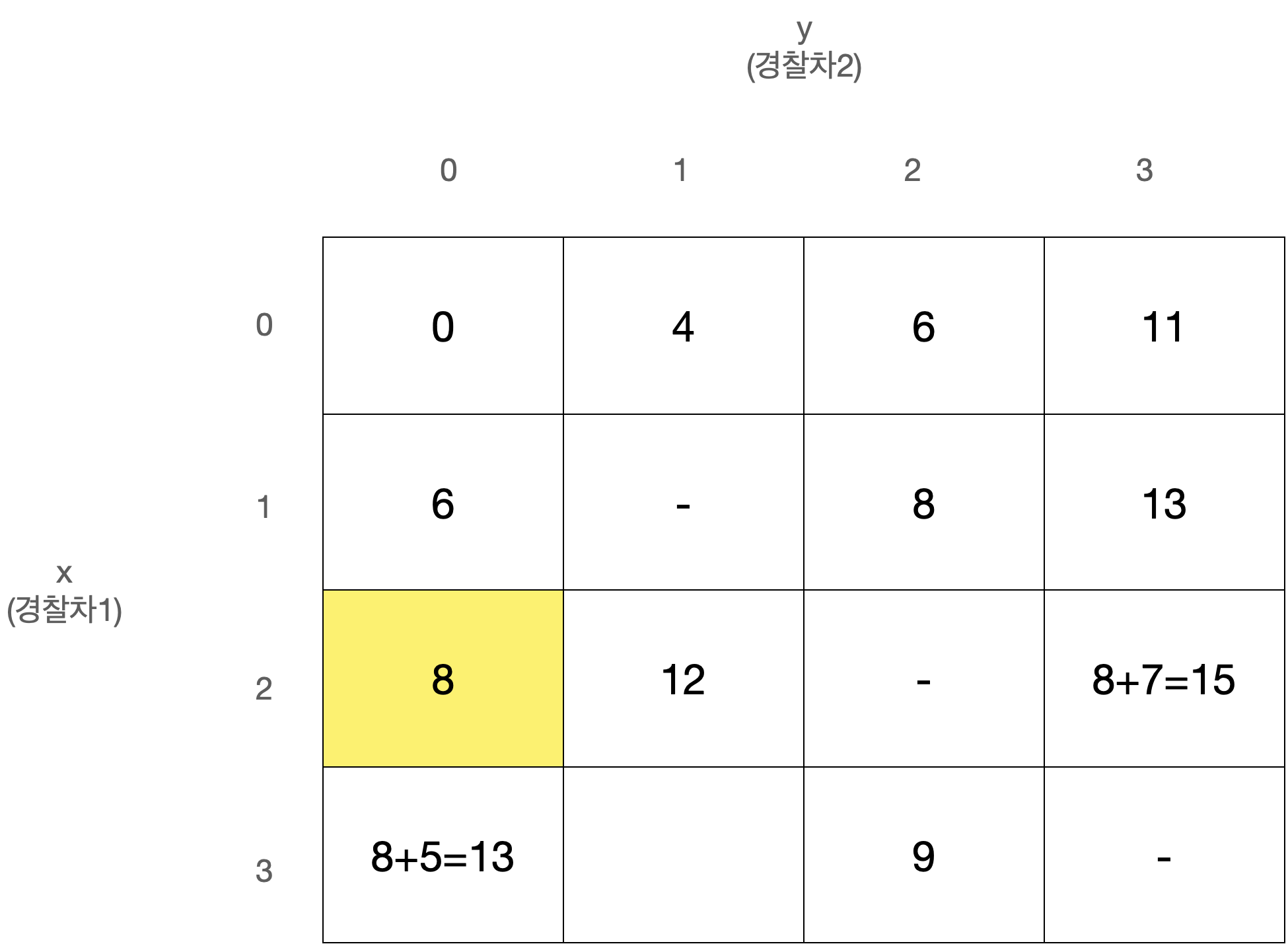
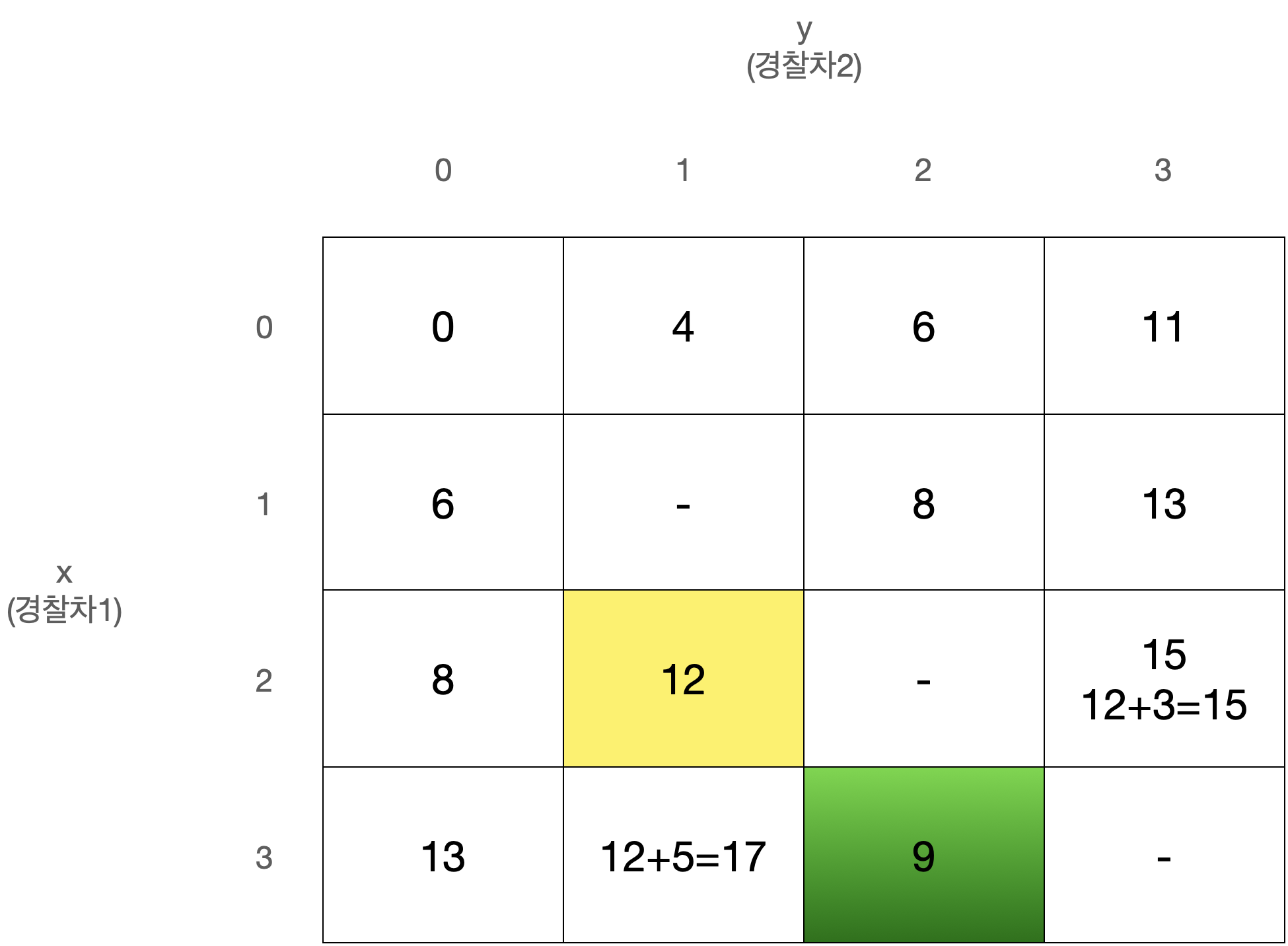
D[x][y]를 경찰차1은 x번째 사건, 경찰차2는 y번째 사건을 마지막으로 처리했을 때 두 경찰차의 이동거리 최소합으로 정의하자.
D[0][0]은 아무 사건도 처리하지 않은 상태로 값은 0일 것이다.
또한 x와 y는 같을 수 없고, 둘 중 더 큰 값이 마지막으로 처리된 사건의 번호이므로 다음에는 번째 사건이 처리되어야 한다.
따라서 아래와 같이 정리된다.
이 점화식을 갖고 아래와 같은 N x N 크기의 2차원 배열 D를 순회하며 값을 채워나가면 된다.

Where to DP? (실문제 해결 사례 소개)
프로젝트 소개
GitHub - hoonww/Gillajab-i: 2021 데이터청년캠퍼스 고려대학교 과정 4조
이 프로젝트는 2021년 여름, 한국데이터산업진흥원에서 운영한 데이터청년캠퍼스라는 활동에서 진행한, 외국인을 위한 한국어 발음 평가 서비스를 개발한 것이다.
한류 콘텐츠(K-pop, K-drama, K-예능 등) 클립의 발화를 듣고 주어지는 한국어, 영어, 로마지 자막을 보며 따라 읽으면 음성 인식 모듈이 유저의 발음을 인식하여 음소 시퀀스를 생성해준다.
나는 이 서비스에서 정답 음소 시퀀스와 유저 발음 음소 시퀀스의 다른 곳을 시각화하여 피드백하는 기능을 개발해야 했다.
예를 들어 ‘날씨가 맑다’는 문장에 대해 올바른 발음인 ‘날씨가 막따’를 외국인이 ‘나루시가 마르그다’라고 발음했다면, ‘ㄴㅏㄹㅜㅅㅣㄱㅏ ㅁㅏㄹㅡㄱㅡㄷㅏ’와 같이 발음이 틀린 곳을 찾아야 했다.
이 문제를 아래에서 소개할 편집거리 알고리즘을 통해 해결할 수 있었다.
편집거리 알고리즘
Levenshtein Distance를 구하는, 두 문자열의 유사도를 판단하는 알고리즘으로 동적계획법이 적용되었다.
편의상 기호를 하나 정의하자.
String = “helloworld” → String(4)=”hell”, String(7)=”hellowo”
String1과 String2를 비교할 때 D[x][y]를 String1(x)을 String2(y)로 만들기 위한 최소 수정 횟수로 정의하자.
String1을 String2로 만들기 위해 많이 바꿔야 한다면 두 문자열의 유사도는 낮고, 그렇지 않다면 유사도가 높다고 할 수 있다.
편집거리 알고리즘의 점화식은 아래와 같다.
위 점화식으로 Dynamic Table을 채우면 아래와 같이 채워지고, 틀린 부분은 최종 답안인 D[n][m]이 계산된 경로를 역추적하며 값을 증가시킨(문자열을 같게 하기 위해 수정을 요구한) 구간을 추려내면 된다.



이 때 참여 못했는데 감사합니다 ㅜㅜ