개요
너비 우선 탐색(Breadth First Search)이란 트리나 그래프의 탐색 방법 중 하나로서 루트 노드에서부터 시작하여 각 노드의 인접한 노드들을 더 이상 방문하지 않은 노드가 없을 때까지 탐색하는 방법이다.
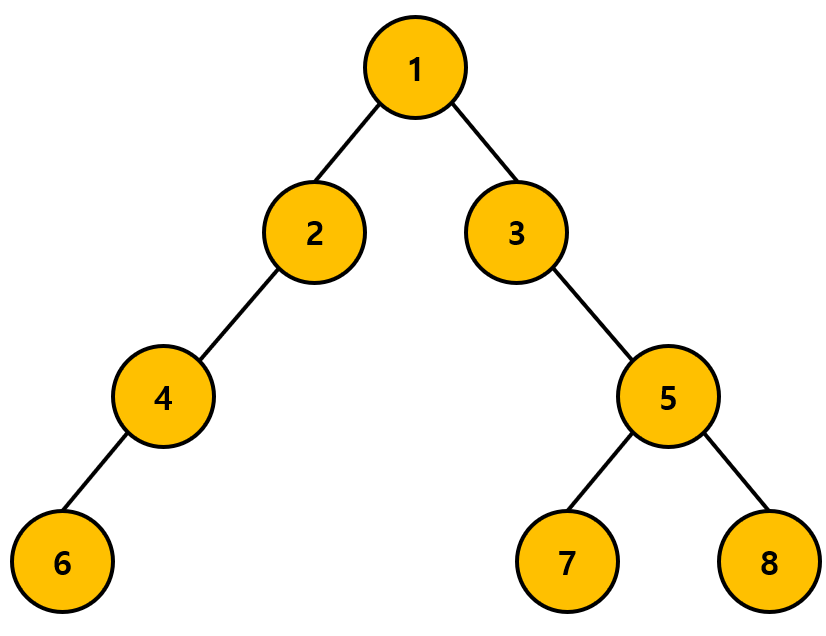
위와 같은 그래프가 있다고 하고 시작 정점을 1이라 하자. 그러면 방문해야 할 노드의 순서 []에 1을 추가한다.
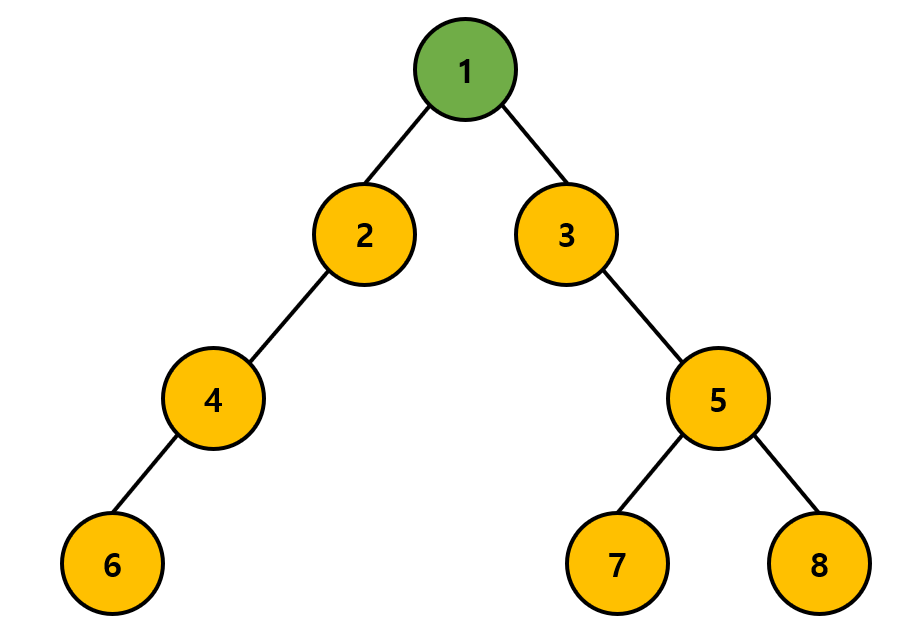
방문해야 할 노드의 순서 [1]에서 가장 앞에 있는 1번 노드를 방문한 다음, 이미 방문한 노드임을 나타낸다. 다음으로 1번 노드와 인접한 노드인 2, 3을 방문해야 할 노드의 순서에 추가한다.
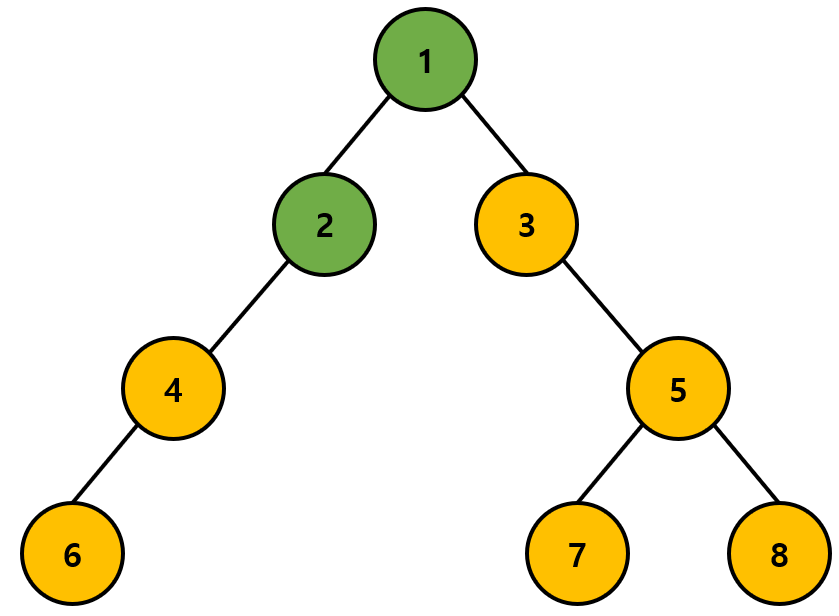
방문해야 할 노드의 순서 [2, 3]에서 가장 앞에 있는 2번 노드를 방문한 다음, 이미 방문한 노드임을 나타낸다. 다음으로 2번 노드와 인접한 노드인 4를 방문해야 할 노드의 순서에 추가한다. 그러면 현재 방문해야 할 노드의 순서는 [3, 4]가 된다.
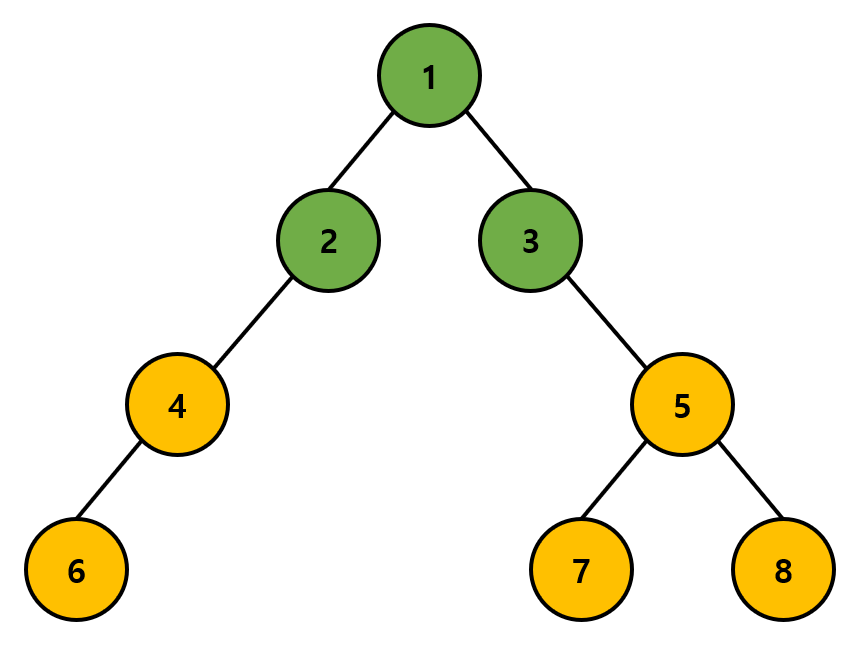
방문해야 할 노드의 순서 [3, 4]에서 가장 앞에 있는 3번 노드를 방문한 다음, 이미 방문한 노드임을 나타낸다. 다음으로 3번 노드와 인접한 노드인 5를 방문해야 할 노드의 순서에 추가한다.
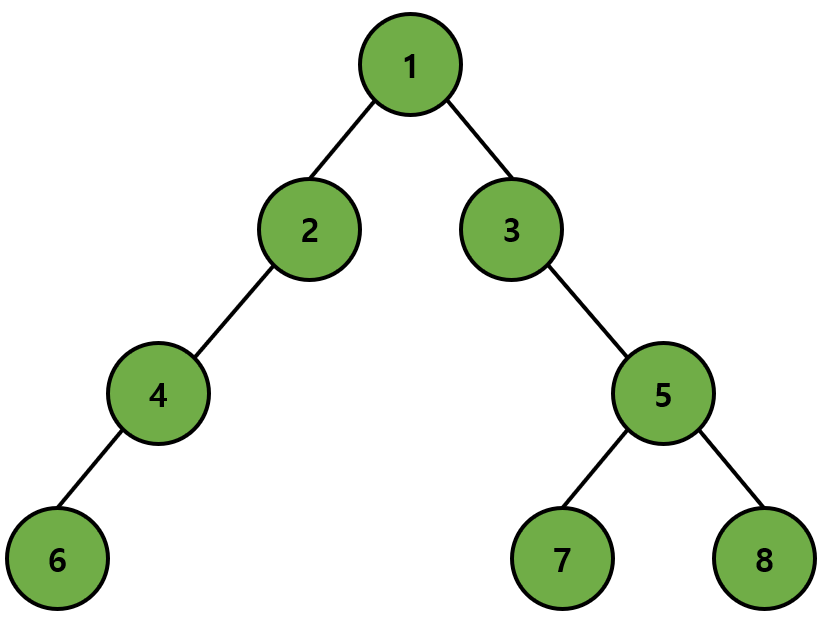
이러한 방식으로 더 이상 방문하지 않은 노드가 없을 때까지 순차적으로 탐색을 진행한다. 그러면 각 노드의 방문 순서는 [1, 2, 3, 4, 5, 6, 7, 8]이 된다.
BFS의 시간 복잡도는 그래프에서 정점의 개수가 V, 간선의 개수가 E라 할 때, O(V+E)로 나타낼 수 있다. 각 정점과 간선을 한 번씩 방문하기 때문이다. 또한, 방문해야 할 노드의 순서를 나타내기 위해 보통 큐(queue)를 구현하여 사용한다. 두 노드 간의 최소 경로를 탐색하거나 이분 그래프임을 판별할 때 BFS를 사용한다.
응용
다음은 BFS를 이용한 문제풀이의 예시이다.
#include <iostream>
#include <queue>
using namespace std;
#define MAXSIZE 51
int farm[MAXSIZE][MAXSIZE];
int Y[] = { -1, 0, 0, 1 };
int X[] = { 0, -1, 1, 0 };
queue<pair<int, int>> q;
int main() {
int t, m, n, k, i, j, x, y, d, cnt = 0;
cin >> t;
while (t) {
cin >> m >> n >> k;
for (i = 1; i <= n; i++) {
for (j = 1; j <= m; j++) {
farm[i][j] = 1;
}
}
for (i = 0; i < k; i++) {
cin >> x >> y;
farm[y + 1][x + 1] = 2;
}
for (i = 1; i <= n; i++) {
for (j = 1; j <= m; j++) {
if (farm[i][j] == 2) {
q.push({ i,j });
farm[i][j] = 1;
while (q.size()) {
x = q.front().second;
y = q.front().first;
q.pop();
for (d = 0; d < 4; d++) {
if (farm[y + Y[d]][x + X[d]] == 2) {
q.push({ y + Y[d], x + X[d] });
farm[y + Y[d]][x + X[d]] = 1;
}
}
}
cnt++;
}
}
}
cout << cnt << '\n';
for (i = 1; i <= n; i++) {
for (j = 1; j <= m; j++) {
farm[i][j] = 0;
}
}
cnt = 0;
t--;
}
return 0;
}2차원 배열의 형태로 나타낸 그래프에서 서로 연결된 정점들의 집합의 개수를 세는 방식이다. 이때의 인접한 노드는 각 점으로부터 대각선을 제외한 1칸씩 상하좌우에 있는 점들이 된다. 배열이 [1][1]부터 시작하는 것은 [0][0]부터 시작하여 존재하지 않는 배열의 인덱스에 접근하는 것을 방지하기 위함이다.
#include <iostream>
#include <queue>
#include <tuple>
using namespace std;
#define MAXSIZE 102
int tomato[MAXSIZE][MAXSIZE][MAXSIZE];
int dx[] = { 0, 0, -1, 1, 0, 0 };
int dy[] = { -1, 1, 0, 0, 0, 0 };
int dz[] = { 0, 0, 0, 0, -1, 1 };
int main() {
int n, m, h, i, j, k, y, x, z, a, b, c, max = -1;
queue<tuple <int, int, int>> q;
cin >> m >> n >> h;
for (k = 0; k < h; k++) {
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++) {
cin >> tomato[i][j][k];
if (tomato[i][j][k] == 1) {
q.push({ i, j, k });
}
}
}
}
while (q.size()) {
x = get<1>(q.front());
y = get<0>(q.front());
z = get<2>(q.front());
q.pop();
for (i = 0; i < 6; i++) {
b = x + dx[i];
a = y + dy[i];
c = z + dz[i];
if ((a >= 0) && (a < n) && (b >= 0) && (b < m) && (c >= 0) && (c < h)) {
if (tomato[a][b][c] == 0) {
tomato[a][b][c] = tomato[y][x][z] + 1;
q.push({ a, b, c });
}
}
}
}
for (k = 0; k < h; k++) {
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++) {
if (max < tomato[i][j][k]) {
max = tomato[i][j][k];
}
if (tomato[i][j][k] == 0) {
max = -1;
break;
}
}
if (j < m) {
break;
}
}
if (i < n) {
break;
}
}
cout << ((max > 0) ? (max - 1) : (max));
return 0;
}탐색을 3차원 배열 상에서 진행한다. 또한, 중간에 탐색을 중단해야 하는 점이 존재한다. 토마토가 있는 점들을 처음의 방문해야 할 노드의 순서에 모두 넣어준 뒤 탐색을 진행하여 가장 멀리 있는 점까지의 거리를 반환하는 방식이다.
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
#define MAXSIZE 105
bool cheese[MAXSIZE][MAXSIZE];
bool check[MAXSIZE][MAXSIZE];
int Y[] = { -1, 0, 0, 1 };
int X[] = { 0, -1, 1, 0 };
queue<pair<int, int>> q;
int allmelt(int n, int m) {
int cnt = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (cheese[i][j]) {
cnt++;
}
}
}
return cnt;
}
void init(int n, int m) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
check[i][j] = false;
}
}
}
int main() {
int n, m, k, x, y, hour = 0, cnt = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> cheese[i][j];
}
}
do {
cnt = allmelt(n, m);
if (cnt == 0) {
break;
}
init(n, m);
q.push({ 1, 1 });
check[1][1] = true;
while (q.size()) {
x = q.front().second;
y = q.front().first;
q.pop();
for (k = 0; k < 4; k++) {
if ((y + Y[k] < 0) || (y + Y[k] > n) || (x + X[k] < 0) || (x + X[k] > m)) {
continue;
}
else if ((cheese[y + Y[k]][x + X[k]] == false) && (check[y + Y[k]][x + X[k]] == false)) {
q.push({ y + Y[k], x + X[k] });
check[(y + Y[k])][(x + X[k])] = true;
}
else if ((cheese[y + Y[k]][x + X[k]] == true) && (check[y + Y[k]][x + X[k]] == false)) {
cheese[(y + Y[k])][(x + X[k])] = false;
check[(y + Y[k])][(x + X[k])] = true;
}
}
}
hour++;
} while (allmelt(n, m));
cout << hour << "\n" << cnt;
return 0;
}처음의 방문해야 할 노드를 어떤 것으로 해야할 지 생각하는 데 긴 시간이 걸렸던 문제다. 바깥 부분과 인접한 부분부터 녹기 때문에 치즈가 없는 점들을 처음의 방문해야 할 노드에 모두 추가한 뒤, 탐색을 진행하여 가장 먼 노드와의 거리, 그 노드를 구하기 전의 배열의 상태에서 치즈의 개수를 구함으로써 해결했다.
#include <bits/stdc++.h>
using namespace std;
int n, weight = 2, stomach = 0, ans = 0;
int aquarium[22][22];
bool visited[22][22];
void bfs(int sy, int sx) {
int y, x, dist;
int dy[] = { -1,0,1,0 };
int dx[] = { 0,-1,0,1 };
queue<pair<pair<int, int>, int>> q;
q.push({ {sy,sx},0 });
visited[sy][sx] = true;
while (1) {
priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;
while (!q.empty()) {
y = q.front().first.first;
x = q.front().first.second;
dist = q.front().second;
q.pop();
for (int i = 0; i < 4; i++) {
if ((y + dy[i] >= 0) && (y + dy[i] < n) && (x + dx[i] >= 0) && (x + dx[i] < n)) {
if (visited[y + dy[i]][x + dx[i]] == false) {
if ((aquarium[y + dy[i]][x + dx[i]] < weight) && (aquarium[y + dy[i]][x + dx[i]] > 0)) {
pq.push({ dist + 1,{y + dy[i],x + dx[i]} });
visited[y + dy[i]][x + dx[i]] = true;
}
else if ((aquarium[y + dy[i]][x + dx[i]] == weight) || (aquarium[y + dy[i]][x + dx[i]] == 0)) {
q.push({ {y + dy[i],x + dx[i]},dist + 1 });
visited[y + dy[i]][x + dx[i]] = true;
}
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
visited[i][j] = false;
}
}
if (pq.empty()) {
return;
}
else {
dist = pq.top().first;
y = pq.top().second.first;
x = pq.top().second.second;
pq.pop();
aquarium[y][x] = 0;
stomach++;
if (stomach == weight) {
weight++;
stomach = 0;
}
ans += dist;
q.push({ {y,x},0 });
visited[y][x] = true;
}
}
}
int main() {
int sy, sx;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> aquarium[i][j];
if (aquarium[i][j] == 9) {
sy = i;
sx = j;
aquarium[i][j] = 0;
}
}
}
bfs(sy, sx);
cout << ans;
return 0;
}힙을 활용하여 문제를 푸는 것이 꽤나 고역이었던 문제였다. 상어의 현재 위치로부터 물고기들의 거리를 힙에 삽입하고 힙에서 가장 최소값을 가진(상어의 현재 위치로부터 가장 거리가 가까운) 노드를 꺼내면서 정답을 계산하는데, 이러한 과정을 힙을 더 이상 만들 수 없을 때(공간에 더 이상 물고기가 없을 때)까지 진행한다.
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;
char lightroom[105][105];
bool check[105][105];
int dist[105][105];
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int w, h, mirror, y, x, head, ans;
vector<pair<int, int>> light;
priority_queue<pair<int, pair<pair<int, int>, int>>, vector<pair<int, pair<pair<int, int>, int>>>, greater<pair<int, pair<pair<int, int>, int>>>> pq;
int dy[] = { -1,0,1,0 };
int dx[] = { 0,-1,0,1 };
cin >> w >> h;
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
cin >> lightroom[i][j];
if (lightroom[i][j] == 'C') {
light.push_back({ i,j });
}
dist[i][j] = INF;
}
}
pq.push({ 0,{{light.at(0).first,light.at(0).second},0} });
pq.push({ 0,{{light.at(0).first,light.at(0).second},1} });
pq.push({ 0,{{light.at(0).first,light.at(0).second},2} });
pq.push({ 0,{{light.at(0).first,light.at(0).second},3} });
dist[light.at(0).first][light.at(0).second] = 0;
check[light.at(0).first][light.at(0).second] = true;
while (!pq.empty()) {
mirror = pq.top().first;
y = pq.top().second.first.first;
x = pq.top().second.first.second;
head = pq.top().second.second;
pq.pop();
if (mirror > dist[y][x]) {
continue;
}
for (int i = 0; i < 4; i++) {
if ((y + dy[i] >= 0) && (y + dy[i] < h) && (x + dx[i] >= 0) && (x + dx[i] < w)) {
if (i == head) {
if ((lightroom[y + dy[i]][x + dx[i]] != '*') && (dist[y + dy[i]][x + dx[i]] >= mirror) && (check[y + dy[i]][x + dx[i]] != true)) {
pq.push({ mirror,{{y + dy[i],x + dx[i]},head} });
dist[y + dy[i]][x + dx[i]] = mirror;
check[y + dy[i]][x + dx[i]] = true;
}
}
else if (i == ((head + 2) % 4)) {
continue;
}
else {
if ((lightroom[y + dy[i]][x + dx[i]] != '*') && (dist[y + dy[i]][x + dx[i]] >= (mirror + 1)) && (check[y + dy[i]][x + dx[i]] != true)) {
pq.push({ mirror + 1,{{y + dy[i],x + dx[i]},i} });
dist[y + dy[i]][x + dx[i]] = (mirror + 1);
}
}
}
}
}
cout << dist[light.at(1).first][light.at(1).second];
return 0;
}다익스트라를 응용하여 풀 수 있었다. 방향을 바꾸는 데 비용이 소모된다고 가정하고 비용을 힙에 삽입함으로써 가장 적은 비용을 소모하면서 목적지까지 갈 수 있는 경로를 탐색한다. 이때, 일직선으로의 경로 탐색은 BFS를 사용했다. 특히 어려운 점은 레이저가 교차하는 점에 대한 경로의 탐색이었다. 이미 지나왔으며, 그보다 낮은 비용의 탐색이 불가능한 경우 방문한 노드임을 표시해주어야 시간 초과없이 문제를 해결할 수 있다.
#include <bits/stdc++.h>
using namespace std;
int r, c;
char lake[1505][1505];
int melting[1505][1505];
bool check[1505][1505];
vector<pair<int, int>> swan;
queue<pair<int, int>> water;
int main() {
int y, x, ans, cnt;
int dy[] = { -1,1,0,0 };
int dx[] = { 0,0,-1,1 };
priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> r >> c;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
cin >> lake[i][j];
if (lake[i][j] == 'L') {
swan.push_back({ i,j });
water.push({ i,j });
melting[i][j] = 0;
}
else if (lake[i][j] == '.') {
water.push({ i,j });
melting[i][j] = 0;
}
else {
melting[i][j] = -1;
}
}
}
while (!water.empty()) {
y = water.front().first;
x = water.front().second;
water.pop();
for (int i = 0; i < 4; i++) {
if ((y + dy[i] >= 0) && (y + dy[i] < r) && (x + dx[i] >= 0) && (x + dx[i] < c)) {
if (melting[y + dy[i]][x + dx[i]] == (-1)) {
melting[y + dy[i]][x + dx[i]] = melting[y][x] + 1;
water.push({ y + dy[i],x + dx[i] });
}
}
}
}
pq.push({ 0,{swan.at(0).first,swan.at(0).second} });
check[swan.at(0).first][swan.at(0).second] = true;
while (!pq.empty()) {
cnt = pq.top().first;
y = pq.top().second.first;
x = pq.top().second.second;
pq.pop();
if ((y == swan.at(1).first) && (x == swan.at(1).second)) {
ans = cnt;
break;
}
for (int i = 0; i < 4; i++) {
if ((y + dy[i] >= 0) && (y + dy[i] < r) && (x + dx[i] >= 0) && (x + dx[i] < c)) {
if (check[y + dy[i]][x + dx[i]] != true) {
pq.push({ max(cnt,melting[y + dy[i]][x + dx[i]]),{y + dy[i],x + dx[i]} });
check[y + dy[i]][x + dx[i]] = true;
}
}
}
}
cout << ans;
return 0;
}이보다 더 효율적인 방법이 반드시 있겠지만, 일단 생각나는 방법대로 해결했기에 효율적이지 못하다고 생각되는 풀이 방법이다. BFS를 통해 얼음이 없는 점들을 처음의 방문해야 할 노드의 순서에 추가하고 순차적으로 탐색을 진행하여 호수의 각 점까지 가는 데 필요한 비용(얼음이 녹는 날)들을 계산한다. 다음으로 다익스트라를 통해 가장 최소의 비용으로 백조 사이의 거리(두 점을 지나기까지 얼음이 녹는 날의 최대값)를 계산한다. 불필요한 점들을 방문해야 하기에 괜찮은 풀이 방법은 아니라고 생각한다.
