
개요
참고 : 너비 우선 탐색 (1)
너비 우선 탐색(Breadth First Search)이란 트리나 그래프의 탐색 방법 중 하나로서 루트 노드에서부터 시작하여 각 노드의 인접한 노드들을 더 이상 방문하지 않은 노드가 없을 때까지 탐색하는 방법이다.
Baekjoon에서 BFS를 이용해 풀 수 있는 문제들과 그에 대한 풀이들을 작성해보자.
응용
#include <iostream>
#include <queue>
using namespace std;
int main() {
int n, a, b, m, x, y, cnt;
bool edge[105][105] = { 0, };
bool visit[105][105];
queue<pair<int, int>> q;
cin >> n;
cin >> a >> b;
cin >> m;
for (int i = 0; i < m; i++) {
cin >> x >> y;
edge[x][y] = 1;
edge[y][x] = 1;
visit[y][x] = false;
visit[x][y] = false;
}
q.push({ a,0 });
while (!q.empty()) {
a = q.front().first;
cnt = q.front().second;
q.pop();
if (a == b) {
cout << cnt;
return 0;
}
for (int i = 1; i <= n; i++) {
if ((edge[a][i] == 1) && (visit[a][i] == false)) {
q.push({ i,cnt + 1 });
visit[a][i] = true;
visit[i][a] = true;
}
}
}
cout << -1;
return 0;
}
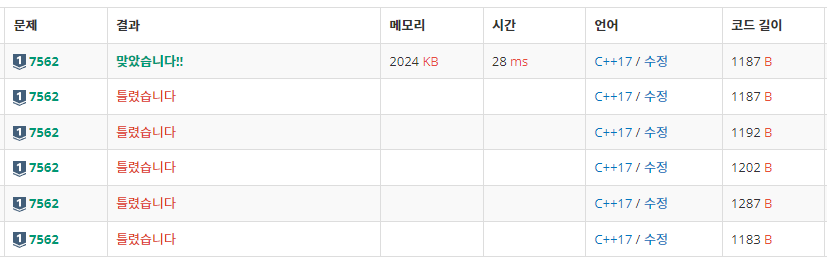
시작점과 도착점(촌수를 찾아야 하는 서로 다른 두 점)이 주어지면 시작점으로부터 연결된 요소들을 탐색하고 연결된 요소들로부터 방문하지 않은 연결된 요소들을 탐색하는, BFS의 기본과 같은 문제. 앞서 WA 1회는 주어지는 점들이 1부터 시작한다는 것을 생각하지 못해 받은 것이다. 문제의 조건을 항상 꼼꼼히 확인하는 습관을 갖자.
#include <iostream>
#include <queue>
#include <tuple>
using namespace std;
int main() {
int t, l, sx, sy, gx, gy, x, y, hx, hy, cnt;
bool check[305][305];
queue<tuple<int, int, int>> q;
int dy[] = { 2,2,1,1,-1,-1,-2,-2 };
int dx[] = { -1,1,-2,2,-2,2,-1,1 };
cin >> t;
while (t--) {
cin >> l;
for (int i = 0; i < l; i++) {
for (int j = 0; j < l; j++) {
check[i][j] = false;
}
}
cin >> sx >> sy;
cin >> gx >> gy;
if ((sy == gy) && (sx == gx)) {
cout << 0 << "\n";
}
else {
q.push({ sy, sx, 0 });
check[sy][sx] = true;
while (!q.empty()) {
y = get<0>(q.front());
x = get<1>(q.front());
cnt = get<2>(q.front());
q.pop();
if ((y == gy) && (x == gx)) {
cout << cnt << "\n";
break;
}
for (int i = 0; i < 8; i++) {
hy = y + dy[i];
hx = x + dx[i];
if ((hy >= 0) && (hy < l) && (hx >= 0) && (hx < l)) {
if (check[hy][hx] == false) {
q.push({ hy, hx, cnt + 1 });
check[hy][hx] = true;
}
}
}
}
while (!q.empty()) {
q.pop();
}
}
for (int i = 0; i < l; i++) {
for (int j = 0; j < l; j++) {
check[i][j] = false;
}
}
}
return 0;
}
마찬가지로 시작점과 도착점이 주어지면 탐색을 진행하여 도착점까지의 최소값을 찾는 BFS 문제. 탐색 경로가 체스에서의 나이트의 이동 경로 8개로 늘어났다는 차이점이 있다. 계속되는 WA에 로직을 잘못 설계했나 싶었지만, 탐색을 진행하지 않는 조건 if ((hy >= 0) && (hy < l) && (hx >= 0) && (hx < l))에 오타가 있어 계속 실패했던 것... 문제의 조건뿐만이 아니라 자신이 작성한 코드도 항상 꼼꼼히 읽자.
#include <bits/stdc++.h>
using namespace std;
int befo[35][35], afte[35][35];
bool check[35][35];
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, m, y, x, p;
bool v = false, ans = true;
queue<pair<int, int>> q;
int dy[] = { -1,1,0,0 }, dx[] = { 0,0,-1,1 };
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> befo[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> afte[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (befo[i][j] != afte[i][j]) {
if (v) {
ans = false;
break;
}
else {
v = true;
p = befo[i][j];
befo[i][j] = afte[i][j];
q.push({ i,j });
check[i][j] = true;
while (!q.empty()) {
y = q.front().first;
x = q.front().second;
q.pop();
for (int k = 0; k < 4; k++) {
if ((y + dy[k] >= 0) && (y + dy[k] < n) && (x + dx[k] >= 0) && (x + dx[k] < m)) {
if ((befo[y + dy[k]][x + dx[k]] == p) && (check[y + dy[k]][x + dx[k]] == false)) {
befo[y + dy[k]][x + dx[k]] = befo[y][x];
q.push({ y + dy[k],x + dx[k] });
check[y + dy[k]][x + dx[k]] = true;
}
}
}
}
i = 0;
j = 0;
}
}
}
if (ans == false) {
break;
}
}
if (ans) {
cout << "YES";
}
else {
cout << "NO";
}
return 0;
}
백신을 접종하기 전의 상태와 접종한 후의 상태가 주어지면, 접종하기 전의 상태에서 BFS를 1회 진행하여 접종한 후의 상태를 만들 수 있는지 확인하는, 약간은 특이한 BFS 문제. 주어지는 상태의 크기 N, M이 1 ≤ N, M ≤ 30 이므로 서로 다른 상태인지 확인하는 데는 큰 시간이 소모되지 않는다. (O(NM)) 둘을 비교하는 중 값이 다를 경우에 BFS를 진행하면 된다. 1회 진행 후에도 값이 다를 경우 BFS로 같은 상태를 만드는 것이 불가능하다고 판단하면 된다. BFS를 진행하면 둘의 비교를 처음부터 진행해주어야 한다는 점을 주의하자. BFS로 앞서 확인한 값들이 변경되었을 수 있으므로 BFS를 시작한 점부터 비교를 재개하면 이전의 값은 확인할 수 없다. WA는 그로 인해 받은 것.
#include <iostream>
#include <string>
#include <queue>
#include <tuple>
using namespace std;
string bomul[55];
int island[55][55];
bool visit[55][55];
void novisit(int h, int w) {
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
visit[i][j] = false;
}
}
}
int main() {
int h, w, y, x, cnt, mcnt;
queue<tuple<int, int, int>> q;
int dx[] = { -1,1,0,0 };
int dy[] = { 0,0,-1,1 };
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> h >> w;
for (int i = 0; i < h; i++) {
cin >> bomul[i];
}
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
if (bomul[i][j] == 'L') {
novisit(h, w);
mcnt = -1;
q.push({ i,j,0 });
visit[i][j] = true;
while (!q.empty()) {
y = get<0>(q.front());
x = get<1>(q.front());
cnt = get<2>(q.front());
mcnt = max(mcnt, cnt);
q.pop();
for (int k = 0; k < 4; k++) {
if ((y + dy[k] < h) && (y + dy[k] >= 0) && (x + dx[k] < w) && (x + dx[k] >= 0)) {
if ((bomul[y + dy[k]][x + dx[k]] == 'L') && (visit[y + dy[k]][x + dx[k]] == false)) {
q.push({ y + dy[k],x + dx[k],cnt + 1 });
visit[y + dy[k]][x + dx[k]] = true;
}
}
}
}
island[i][j] = mcnt;
}
else {
island[i][j] = 0;
}
}
}
mcnt = -1;
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
mcnt = max(mcnt, island[i][j]);
}
}
cout << mcnt;
return 0;
}
육지의 모든 점으로부터 BFS를 진행하여 탐색이 가능한 가장 먼 거리를 반환하는 문제. 모든 점에서 탐색을 진행하므로 시간복잡도가 상당히 클 것 같았지만 (O(n²m²) ← Thanks to bon0057), 가로와 세로의 최대 크기가 50이므로 6250000번 계산되면 TLE 없이 해결 가능하다.
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
char maze[1005][1005];
int imaze[1005][1005];
bool visit[1005][1005];
bool firevisit[1005][1005];
int main() {
int r, c, y, x, cnt;
queue<pair<int, int>> fire;
vector<pair<int, int>> firstfire;
queue<pair<pair<int, int>, int>> jihoon;
int dy[] = { -1,1,0,0 };
int dx[] = { 0,0,-1,1 };
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> r >> c;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
cin >> maze[i][j];
visit[i][j] = false;
if (maze[i][j] == 'J') {
jihoon.push({ { i,j },0 });
visit[i][j] = true;
firevisit[i][j] = false;
imaze[i][j] = 0;
}
else if (maze[i][j] == 'F') {
fire.push({ i,j });
firstfire.push_back({ i,j });
firevisit[i][j] = true;
}
else if (maze[i][j] == '#') {
imaze[i][j] = -1;
}
else {
imaze[i][j] = 0;
firevisit[i][j] = false;
}
}
}
if (fire.size()) {
while (!fire.empty()) {
y = fire.front().first;
x = fire.front().second;
fire.pop();
for (int i = 0; i < 4; i++) {
if ((y + dy[i] >= 0) && (y + dy[i] < r) && (x + dx[i] >= 0) && (x + dx[i] < c)) {
if (imaze[y + dy[i]][x + dx[i]] == 0) {
imaze[y + dy[i]][x + dx[i]] = imaze[y][x] + 1;
fire.push({ y + dy[i],x + dx[i] });
firevisit[y + dy[i]][x + dx[i]] = true;
}
}
}
}
for (int i = 0; i < firstfire.size(); i++) {
imaze[firstfire.at(i).first][firstfire.at(i).second] = 0;
}
}
while (!jihoon.empty()) {
y = jihoon.front().first.first;
x = jihoon.front().first.second;
cnt = jihoon.front().second;
jihoon.pop();
for (int i = 0; i < 4; i++) {
if ((y + dy[i] < 0) || (y + dy[i] >= r) || (x + dx[i] < 0) || (x + dx[i] >= c)) {
cout << cnt + 1;
return 0;
}
else {
if ((imaze[y + dy[i]][x + dx[i]] != (-1)) && ((firevisit[y + dy[i]][x + dx[i]] == false) || ((cnt + 1) < imaze[y + dy[i]][x + dx[i]])) && (visit[y + dy[i]][x + dx[i]] == false)) {
jihoon.push({ {y + dy[i],x + dx[i]},cnt + 1 });
visit[y + dy[i]][x + dx[i]] = true;
}
}
}
}
cout << "IMPOSSIBLE";
return 0;
}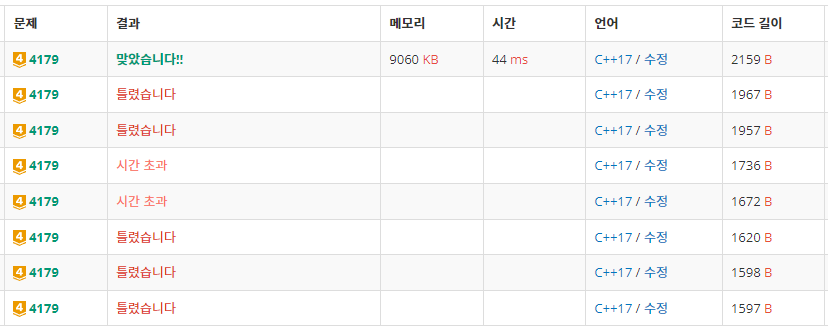
미로의 크기, 불과 지훈이의 위치가 주어지면 지훈이가 주어진 미로를 벗어나는 최단 경로를 계산해야 한다. 이때, 지훈이뿐만 아니라 불도 BFS를 진행해야 한다. 처음에는 지훈이의 위치와 모든 불의 위치를 받고난 뒤, 지훈이의 탐색이 진행되고 나면 모든 불에 BFS를 적용하고 탐색이 끝난 뒤의 위치들을 저장하는 방식으로 로직을 구현했다. 하지만 생각보다 로직을 구현하기가 어려웠으며(지훈이가 빠른지, 불이 빠른지, 즉 어느 것의 탐색을 더 우선으로 해야하는지 고민해야 했기 때문) 코드가 복잡해지는 느낌이 들어 로직을 수정하기로 했다. 처음부터 모든 불에 대해 BFS를 진행하며 불이 몇번째 턴에 미로의 각 위치에 도착하는지 저장하는 2차원 배열을 생성한다. 다음으로 지훈이의 BFS를 진행하는데 이동이 불가능한 위치는 벽과 현재 지훈이의 걸음수, 즉 앞선 턴에 옮겨붙은 불의 위치가 되는 것이다. 해당 로직대로 구현했지만 불의 BFS를 진행할 때 방문 여부를 확인하지 않는 실수를 해서 불필요하게 많은 WA를 받게 되었다. 제출 전 코드 확인은 늘 꼼꼼히 하자.
#include <bits/stdc++.h>
using namespace std;
int main() {
int test_case, n, m, tmp, d, s, l, r;
bool check[10005];
int dslr[10005];
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> test_case;
while (test_case--) {
vector<char> ans;
queue<int> q;
for (int i = 0; i < 10000; i++) {
check[i] = false;
}
cin >> n >> m;
check[n] = true;
dslr[n] = n;
q.push(n);
while (!q.empty()) {
tmp = q.front();
q.pop();
if (tmp == m) {
break;
}
d = (tmp * 2) % 10000;
s = (tmp == 0) ? (9999) : (tmp - 1);
l = (tmp % 1000) * 10 + (tmp / 1000);
r = (tmp / 10) + (tmp % 10) * 1000;
if (check[d] == false) {
check[d] = true;
dslr[d] = tmp;
q.push(d);
}
if (check[s] == false) {
check[s] = true;
dslr[s] = tmp;
q.push(s);
}
if (check[l] == false) {
check[l] = true;
dslr[l] = tmp;
q.push(l);
}
if (check[r] == false) {
check[r] = true;
dslr[r] = tmp;
q.push(r);
}
}
tmp = m;
while (tmp != dslr[tmp]) {
if (((dslr[tmp] * 2) % 10000) == tmp) {
ans.push_back('D');
}
else if (((dslr[tmp] == 0) ? (9999) : (dslr[tmp] - 1)) == tmp) {
ans.push_back('S');
}
else if (((dslr[tmp] % 1000) * 10 + (dslr[tmp] / 1000)) == tmp) {
ans.push_back('L');
}
else if (((dslr[tmp] / 10) + (dslr[tmp] % 10) * 1000) == tmp) {
ans.push_back('R');
}
tmp = dslr[tmp];
}
int k = (int)ans.size() - 1;
for (int i = k; i >= 0; i--) {
cout << ans.at(i);
}
cout << "\n";
}
return 0;
}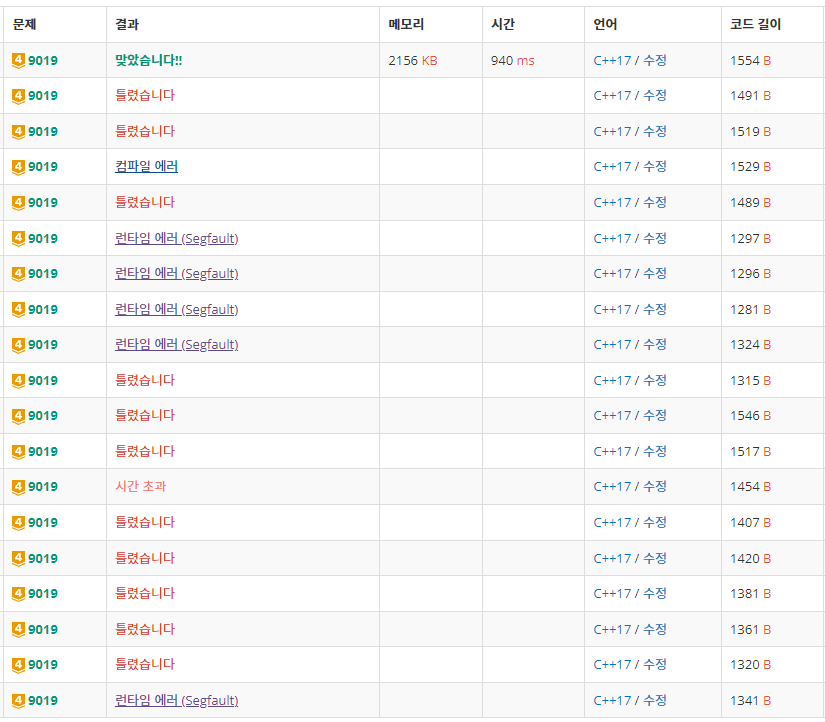
각 테스트 케이스에 대해 초기 값, 최종 값이 주어지면 D, S, L, R 연산을 진행하여 초기 값으로부터 최종 값까지 연산을 최소 몇 번 적용해야 하는지 계산하는 문제이다. 풀이에서 채택한 방식은 10000개 사이즈의 int 배열(dslr[])을 두고 초기 값으로부터 최종 값까지 BFS를 진행한다. 이때, 방문했음을 확인하는 과정에서 앞서 만든 배열의 연산을 적용한 수의 인덱스에 연산을 적용하기 이전의 수를 저장한다. 그리고 최소한의 명령어 나열을 출력하는 과정에서 최종 값으로부터 초기 값까지 역추적을 실시한다. 당시에는 BFS를 진행하면서 파라미터로 계산을 위해 필요한 명령어 나열 string을 전달할 수 없다고 생각해서 불필요하게 복잡한 방법을 채택했다. 그냥 BFS 파라미터로 명령어 나열을 전달하고 최종값을 찾으면 해당 나열을 반환하는 식으로 작성하는 게 낫다.
Baekjoon) 14442 : 벽 부수고 이동하기 2
#include <iostream>
#include <string>
#include <queue>
#include <tuple>
#include <vector>
#include <algorithm>
using namespace std;
bool maze[1005][1005];
int dist[1005][1005][15];
bool visit[1005][1005][15];
int main() {
int n, m, p, y, x, punch;
string mm;
queue<tuple<int, int, int>> q;
vector<int> ans;
int dy[] = { -1,1,0,0 };
int dx[] = { 0,0,-1,1 };
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m >> p;
for (int i = 0; i < n; i++) {
cin >> mm;
for (int j = 0; j < m; j++) {
maze[i][j] = mm[j] - '0';
}
}
q.push({ 0,0,p });
dist[0][0][p] = 1;
visit[0][0][p] = true;
while (!q.empty()) {
y = get<0>(q.front());
x = get<1>(q.front());
punch = get<2>(q.front());
q.pop();
if ((y == (n - 1)) && (x == (m - 1))) {
ans.push_back(dist[y][x][punch]);
}
for (int i = 0; i < 4; i++) {
if ((y + dy[i] >= 0) && (y + dy[i] < n) && (x + dx[i] >= 0) && (x + dx[i] < m)) {
if ((maze[y + dy[i]][x + dx[i]] == 0) && (visit[y + dy[i]][x + dx[i]][punch] != true)) {
q.push({ y + dy[i],x + dx[i],punch });
dist[y + dy[i]][x + dx[i]][punch] = dist[y][x][punch] + 1;
visit[y + dy[i]][x + dx[i]][punch] = true;
}
else {
if ((punch > 0) && (visit[y + dy[i]][x + dx[i]][punch - 1] != true)) {
q.push({ y + dy[i],x + dx[i],punch - 1 });
dist[y + dy[i]][x + dx[i]][punch - 1] = dist[y][x][punch] + 1;
visit[y + dy[i]][x + dx[i]][punch - 1] = true;
}
}
}
}
}
if (ans.empty()) {
cout << -1;
}
else {
sort(ans.begin(), ans.end());
cout << ans.at(0);
}
return 0;
}
0과 1로 주어진 미로가 주어지면 가장 왼쪽 위 점에서 가장 오른쪽 아래 점으로 1을 경유하지 않고 도착하는 최단 거리를 구하는 문제. 하지만, K개의 1을 무시하고 갈 수 있다. 문제에서 K의 범위가 1 ≤ K ≤ 10 이므로 출발점으로부터 각 점까지의 최단 경로를 저장하는 배열의 최대 크기가 [1000][1000]일 때 K개 만큼의 벽을 부수고 지나갔을 때의 최단 경로를 저장하기 위한 배열을 선언하면 최대 크기는 [1000][1000][10]로 메모리 제한을 초과하지 않는다. 따라서, K개 만큼의 벽을 부수고 지나갔을 때의 최단 경로를 저장하는 배열에 최단 경로를 저장하고 정답에는 오른쪽 아래에 도착한 이동거리 중 가장 짧은 것을 출력하면 된다. 하단의 CE와 WA는 정답을 출력하는 과정에서 사용한 sort 함수를 지원하는 라이브러리 algorithm을 선언해주지 않았기 때문이다.
Baekjoon) 16985 : Maaaaaaaaaze
#include <iostream>
#include <queue>
#include <vector>
#include <tuple>
#include <algorithm>
using namespace std;
int ans = 2e9;
bool permu[5][4];
vector<pair<int, int>> makemaze;
bool maze[5][4][5][5];
void escape() {
int z, y, x, cnt, r = 0;
int dz[] = { -1,1,0,0,0,0 };
int dy[] = { 0,0,-1,1,0,0 };
int dx[] = { 0,0,0,0,-1,1 };
queue<pair<tuple<int, int, int>, int>> q;
bool visit[5][5][5];
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
for (int k = 0; k < 5; k++) {
visit[i][j][k] = false;
}
}
}
if (maze[makemaze.at(0).first][makemaze.at(0).second][0][0]) {
q.push({ {0,0,0},0 });
visit[0][0][0] = true;
}
while (!q.empty()) {
z = get<0>(q.front().first);
y = get<1>(q.front().first);
x = get<2>(q.front().first);
cnt = q.front().second;
q.pop();
if ((z == 4) && (y == 4) && (x == 4)) {
ans = min(ans, cnt);
break;
}
for (int i = 0; i < 6; i++) {
if ((z + dz[i] >= 0) && (z + dz[i] < 5) && (y + dy[i] >= 0) && (y + dy[i] < 5) && (x + dx[i] >= 0) && (x + dx[i] < 5)) {
if ((maze[makemaze.at(z + dz[i]).first][makemaze.at(z + dz[i]).second][y + dy[i]][x + dx[i]]) && (visit[z + dz[i]][y + dy[i]][x + dx[i]] == false)) {
q.push({ {z + dz[i],y + dy[i],x + dx[i]},cnt + 1 });
visit[z + dz[i]][y + dy[i]][x + dx[i]] = true;
}
}
}
}
while (!q.empty()) {
q.pop();
}
}
void stacking(int p) {
if (p == 5) {
escape();
}
else {
for (int i = 0; i < 4; i++) {
if (permu[p][i] == false) {
makemaze.at(p).second = i;
stacking(p + 1);
}
}
}
}
int main() {
vector<int> floor = { 0,1,2,3,4 };
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
for (int k = 0; k < 5; k++) {
cin >> maze[i][0][j][k];
}
}
for (int n = 1; n < 4; n++) {
for (int j = 0; j < 5; j++) {
for (int k = 0; k < 5; k++) {
maze[i][n][j][k] = maze[i][(n - 1)][(5 - (k + 1))][j];
}
}
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 4; j++) {
permu[i][j] = false;
}
}
do {
for (int i = 0; i < floor.size(); i++) {
makemaze.push_back({ floor.at(i), 0 });
}
stacking(0);
makemaze.clear();
} while (next_permutation(floor.begin(), floor.end()));
if (ans == 2e9) {
cout << -1;
}
else {
cout << ans;
}
return 0;
}
5개의 미로를 받아 어떠한 순서로 쌓을지, 몇 층의 미로를 어떠한 방향으로 회전시킬지, 모든 경우의 수를 고려해야 정답을 찾을 수 있다. 이를 위해 미로를 입력받는 과정에서 각 미로를 회전시켰을 때의 형태를 따로 저장한다.
for (int n = 1; n < 4; n++) {
for (int j = 0; j < 5; j++) {
for (int k = 0; k < 5; k++) {
maze[i][n][j][k] = maze[i][(n - 1)][(5 - (k + 1))][j];
}
}
}다음으로 재귀를 통해 미로를 조합한다.
vector<int> floor = { 0,1,2,3,4 };
do {
for (int i = 0; i < floor.size(); i++) {
makemaze.push_back({ floor.at(i), 0 });
}
stacking(0);
makemaze.clear();
} while (next_permutation(floor.begin(), floor.end()));next_permutation을 활용하면 1층에서부터 5층까지를 이루는 수열(5!)을 사용하여 탐색할 수 있다. makemaze가 만들어진 5개층의 미로가 되는 것이다. 이 과정에서 stacking 함수로 몇 번째 층의 판을 회전시킬지, 즉 앞서 만들어진 입력된 미로와 회전된 상태의 미로 3개 총 4개 중 어떤 것을 선택할 지 DFS를 진행하는 것이다.
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 4; j++) {
permu[i][j] = false;
}
}
void stacking(int p) {
if (p == 5) {
escape();
}
else {
for (int i = 0; i < 4; i++) {
if (permu[p][i] == false) {
makemaze.at(p).second = i;
stacking(p + 1);
}
}
}
}이렇게 생성된 makemaze에서 탈출을 위한 BFS escape()를 진행하는 것이다. 처음에는 계산할 범위도 컸으며, 회전한 상태의 미로를 어떻게 구현할지, 모든 경우의 수를 확인하는 만큼 TLE가 나지 않을지 굉장히 고민했다. 이 코드를 작성하고 난 뒤 IDE로 실행했을 때에도 정답을 계산하는 데 시간이 한참 걸렸기 때문에 당연히 TLE를 받을거라 생각했다. 하지만 5!×4⁵×5×5 = 3072000 이므로 시간 제한보다 넉넉하게 해결할 수 있다.
References
xavier.log) [C/C++] 백준 2589번 보물섬
AudiosML) BOJ 16985 Maaaaaaaaaze
