SeoulNolgoat 서비스는 서울 내에서 1차, 2차, 3차 회식 가게를 추천해준다.
이때, 이용자의 현재 위치 근처에 있는 가게들을 조합해서
이 조합들을 특정 기준에 맞춰서 정렬한다.
정렬 기준은 거리순/평점순이다.
거리는 현재 위치에서 1차, 2차, 3차 가게로 가는 데 걸리는 시간을 기준으로 하는데, 가까운 순서로 정렬한다.
평점은 서울놀곳의 평점이나 카카오맵에 있는 평점을 기준으로 정렬해서, 높은 평점 순으로 정렬한다.
정렬을 하려면 어떤 알고리즘을 써야 할까?
정렬 알고리즘 정리
참고: [Java/알고리즘] 정렬 알고리즘(Sort Algorithm) 이해하기 -1 : 기본 구조 및 종류
퀵 정렬
분할 정복을 사용하는 알고리즘으로 대규모 데이터 정렬에 유용하다.
분할정복이란?
: 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
순서
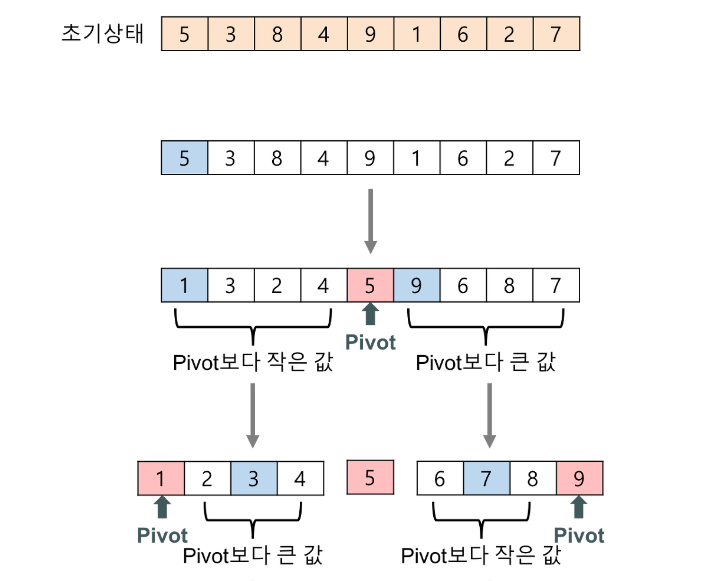
1) 배열에서 하나의 원소를 고른다. 이렇게 고른 원소가 피벗(pivot) 이다.
2) 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 배열을 둘로 나눈다. 이렇게 배열을 둘로 나누는 것을 분할(Divide) 이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
3) 분할된 두 개의 작은 배열에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다
시간복잡도: O(nlogn), 최악의 경우 : O(n^2)
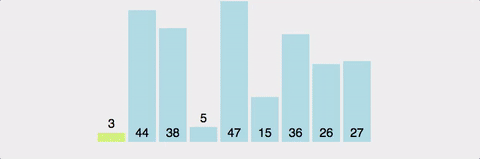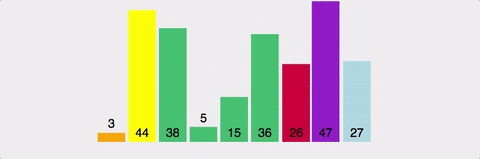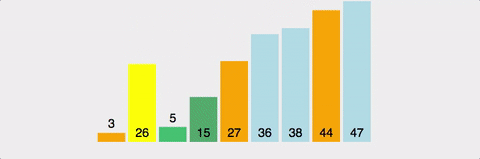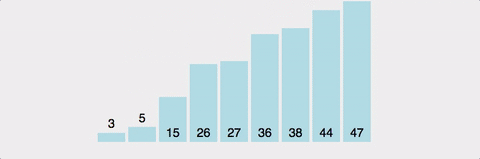
레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k) 했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다.
이것을 일반화하면 n=2^k의 경우, k(k=log₂n) 임을 알 수 있다.
각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
따라서, 최선의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n 가 된다. 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다.
최악의 경우(Worst cases) : T(n) = O(n^2)
최악의 경우는 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있는 경우다.
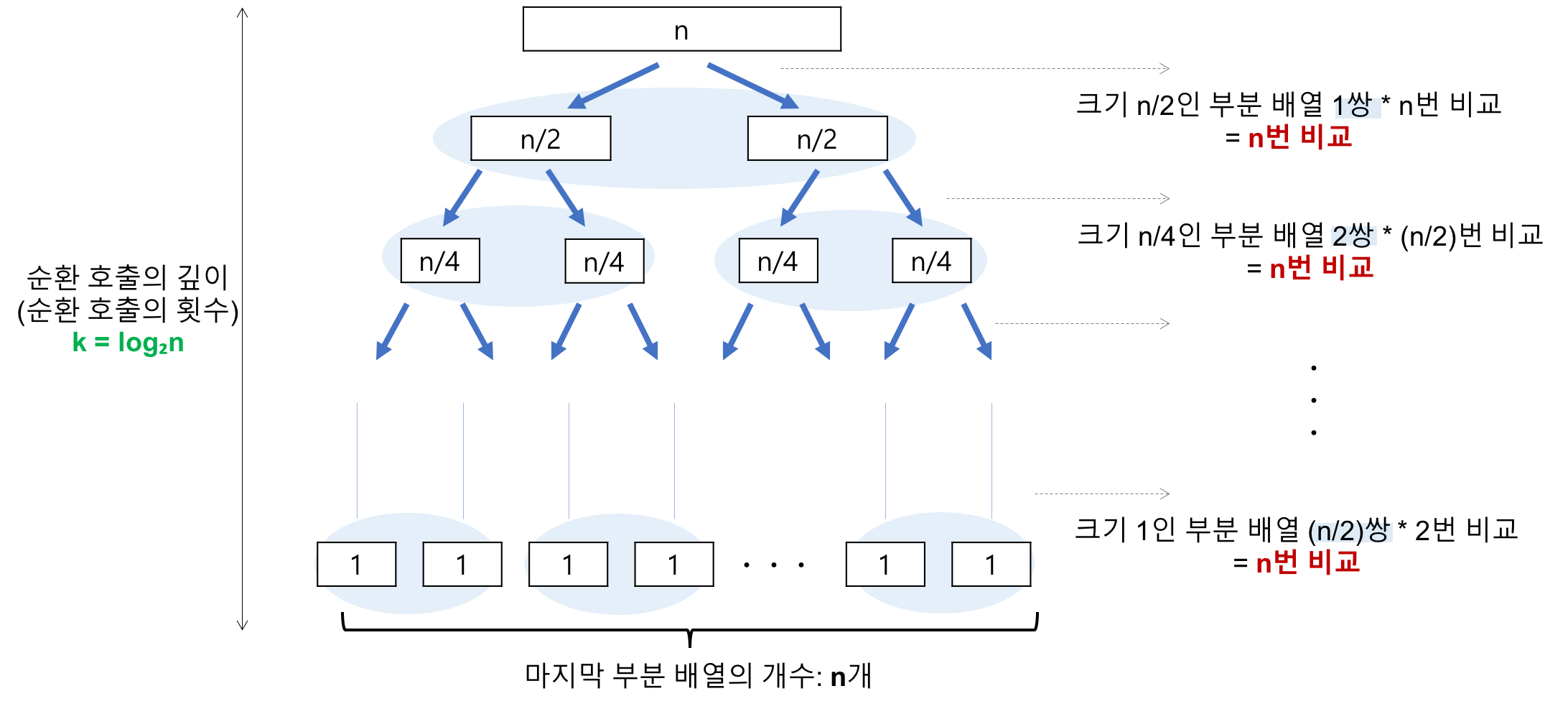
레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n 임을 알 수 있다.
각 순환 호출 단계의 비교 연산 (n)
각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
따라서, 최악의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2 다. 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다.
버블 정렬
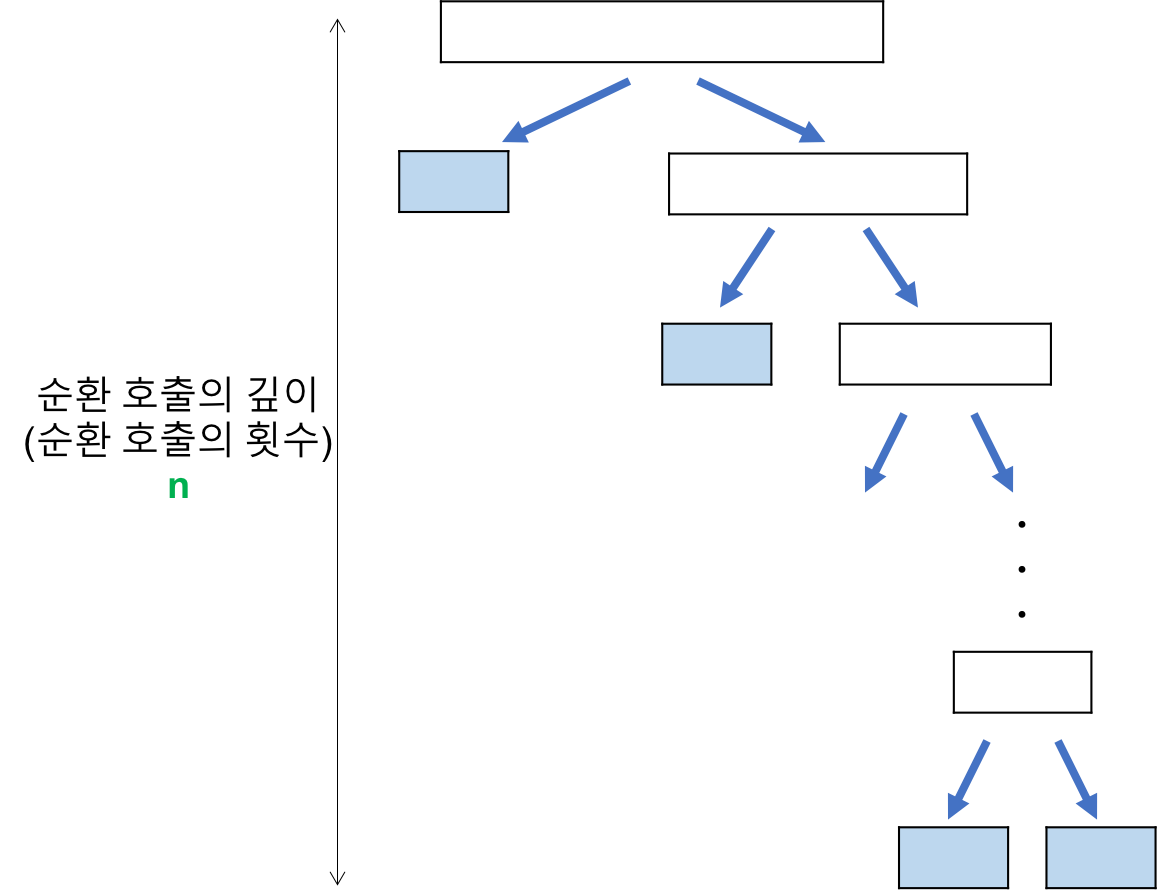
인접한 두 원소를 비교해서 필요한 경우 위치를 교환해 정렬한다.
정렬한 원소의 개수가 적거나, 정렬할 원소의 개수가 많더라도 이미 거의 정렬된 상태일 때 사용한다.
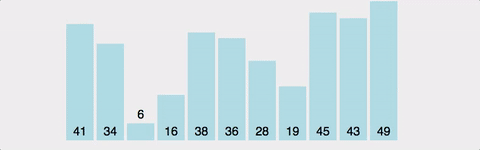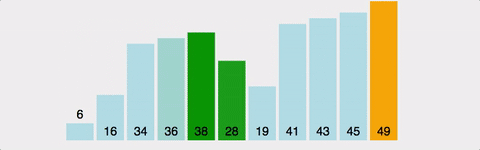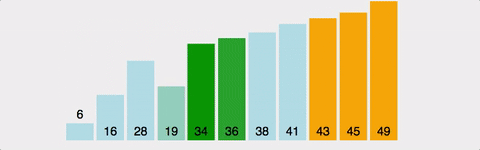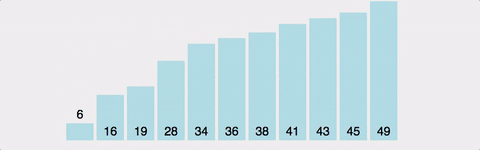
*시간복잡도를 계산하면, (n-1) + (n-2) + (n-3) + .... + 2 + 1 => n(n-1)/2이므로, O(n^2) 이다. 또한, Bubble Sort는 정렬이 돼있던 안돼있던, 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일하다. (개선된 Bubble Sort가 존재하긴 하나, 기초를 다지기 위한 학습이므로 넘어가겠음)
선택 정렬
배열의 최초값을 찾아서 맨 앞의 원소와 자리를 바꾸고 그 다음으로 작은 값을 찾아서 두번째 원소와 자리를 바꾸는 방식
원소의 개수가 적거나, 이미 거의 정렬된 상태에서 사용
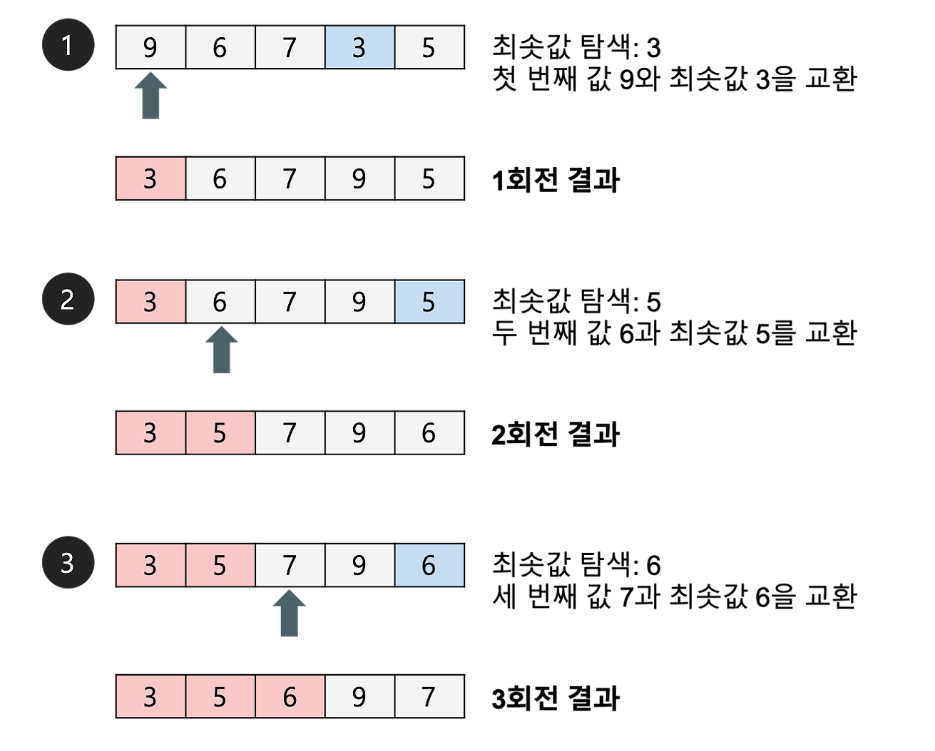
- 시간 복잡도 --> 이 작업을 최대 n - 1 번 반복하면 정렬 O(n^2)
삽입 정렬
정렬되지 않은 부분에서 값을 선택하고 그 값을 이미 정렬된 부분의 올바른 위치에 삽입하는 과정
*시간 복잡도 -->이 작업을 최대 n-1번 반복 O(n^2)
병합 정렬
배열을 반으로 나누어서 각각을 정렬한 후 병합하는 과정을 통해 전체 배열을 정렬한다.
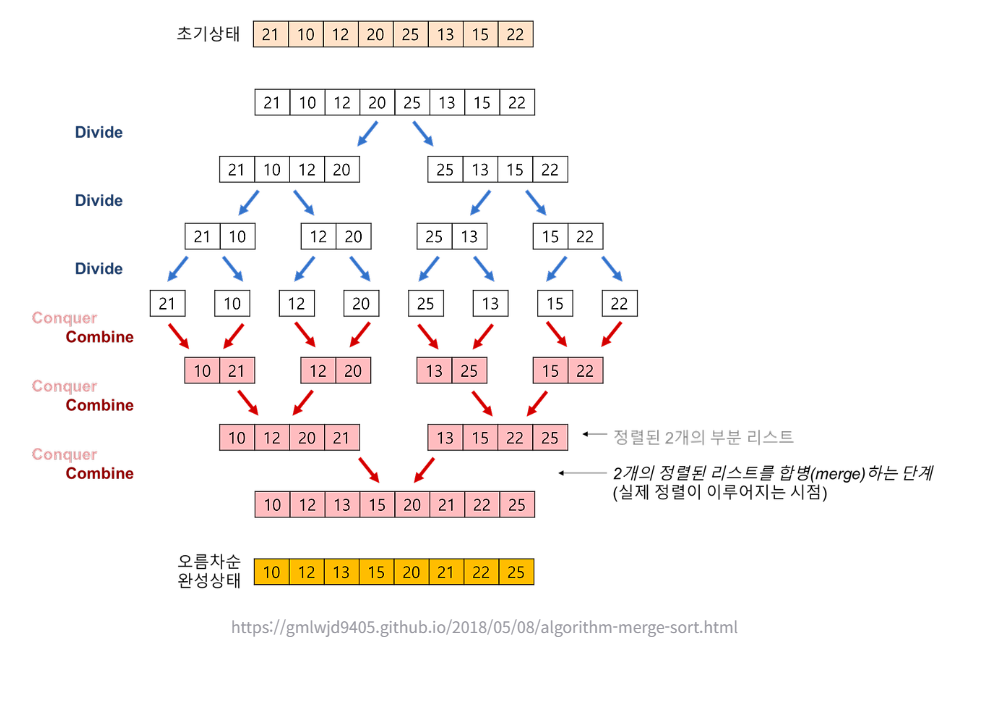
시간복잡도 : O(nlogn)