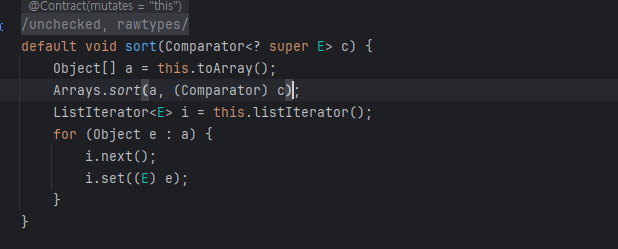
Tim Sort 알고리즘
Arrays.sort()
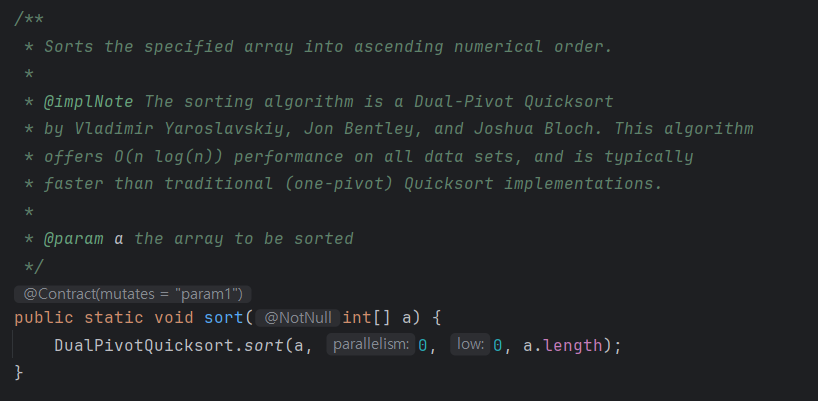
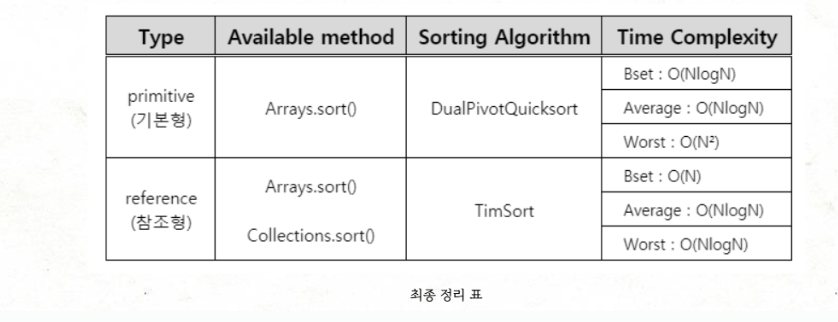
Dual Pivot QuickSort를 사용한 정렬 방식으로 보통 QuickSort보다 더 빠르지만, 최악의 경우 O(n^2)이 발생할 수 있다. 듀얼 피벗정렬은 피벗을 2개 사용해서 정렬을 수행한다.
참고 : [Java] Arrays.sort()와 Collections.sort()에 대해서 자세히 알아보자!
Quicksort는 최악의 경우 O(N²), 평균적으로 O(NlogN)의 시간 복잡도를 가진다.
DualPivotQuicksort은 랜덤 데이터에 대해 일반적인 Quicksort보다 나은 시간 복잡도를 보장하지만, 여전히 최악의 경우 시간 복잡도 O(NlogN)를 가진다.
그러므로 만약에 정렬 알고리즘 문제 등등과 같이 시간 복잡도 O(NlogN)을 보장하는 정렬 코드를 작성해야 한다면 기본형 타입의 배열을 Arrays.sort()로 정렬하는 것은 다시 한번 생각해야 한다.
사실 내부 로직을 깊게 파고들면 배열의 크기에 따라서 적용되는 정렬이 달라지지만 Arrays.sort()를 단순하게 사용하는 경우라면 나중에 필요에 의해서 소스코드를 분석해보는 것을 추천한다.
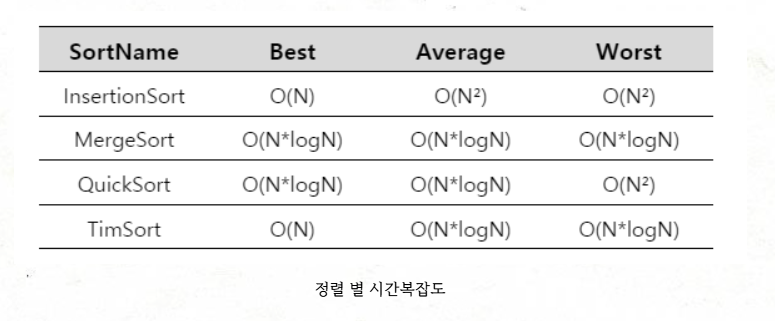
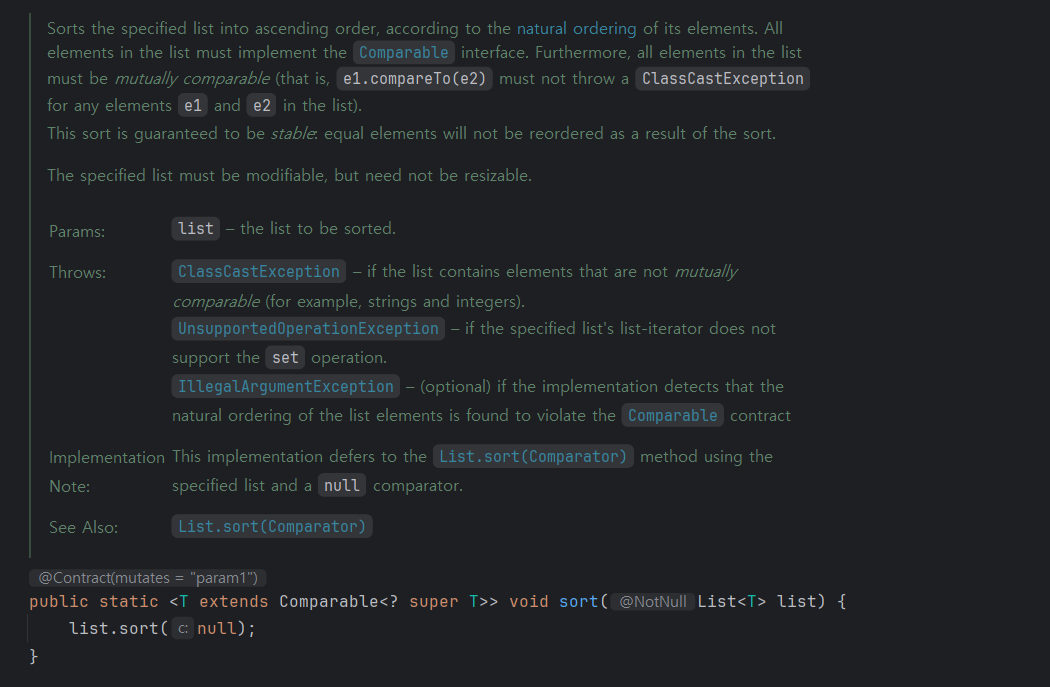
TimSort는 최선의 상태에서는 삽입 정렬의 시간 복잡도 O(N)를 최악의 경우에는 병합 정렬의 시간 복잡도 O(NlogN)을 가진다.
최악의 경우에도 O(NlogN) 시간 복잡도를 가지는 정렬 알고리즘이 필요하다면 Arrays.sort()가 TimSort를 수행할 수 있도록 primitive타입의 배열보단 reference타입의 배열을 사용해야 한다.
Collections.sort()
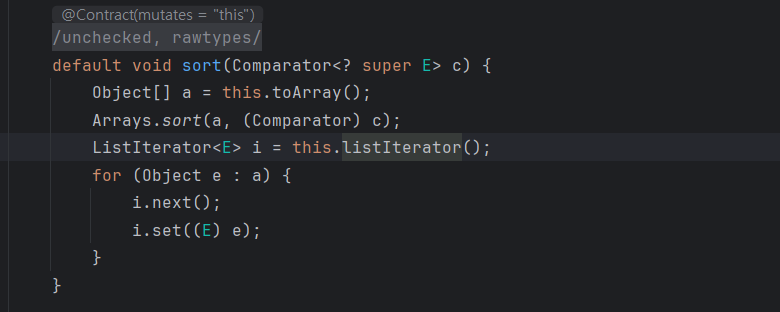
TimeSort 라는 삽입정렬과 병합정렬을 결합한 정렬방식을 사용한다.
시간복잡도는 평균, 최악의 상황에 상관없이 O(nlogn)을 갖는다.
대신 배열에서 사용할 수 없고, List, Map 등의 컬렉션 프레임워크의 구조에서 사용 가능
내부적으로 list.sort가 쓰이는데, 이 api를 보면 내부에 Arrays.sort를 쓰는 것을 알 수 있다.
즉, Collections.sort()에서는 List객체를 Object배열로 변환해서 Arrays.sort()를 실행해서 정렬을 수행합니다.
Arrays.sort() 내부를 살펴보면 다음과 같이 TimSort.sort()를 실행하는 걸 볼 수 있습니다.
Tim sort에 대한 정리
참조 : Tim sort에 대해 알아보자
Tim sort는 Merge sort를 기반으로 하되, 여러 최적화 기법을 적용했다.
배열을 작은 덩어리(run)로 나누고, 이를 효율적으로 병합한다.
(1) Heap sort
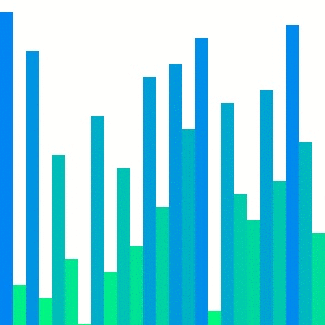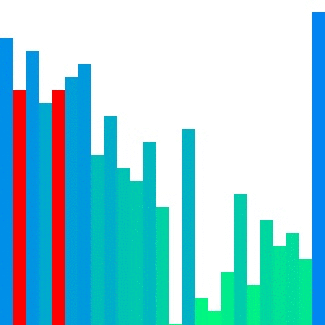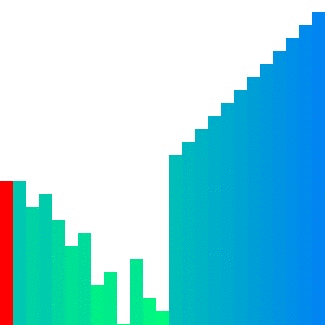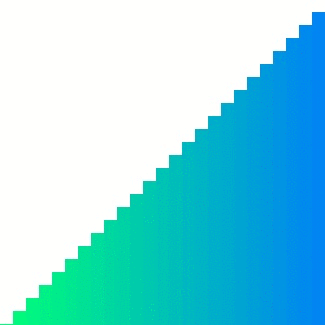
Heap sort는 참조지역성이 좋지 않은 정렬이다. 한 위치에 있는 요소를 해당 요소의 인덱스 두 배 또는 절반인 요소와 바녹적으로 비교하기에 캐시 메모리에서는 예츠가기가 어렵다.
시간 복잡도가 O(nlogn)이라는 말은 실제 동작 시간은 C×nlogn+α라는 의미이다. 상대적으로 무시할 수 있는 부분인 α 부분을 제하면 nlogn에는 앞에 C라는 상수가 곱해져 있어 이 값에 따라 실제 동작 시간에 큰 차이가 생긴다. 이 C라는 값에 큰 영향을 끼치는 요소로 '알고리즘이 참조 지역성(Locality of reference) 원리를 얼마나 잘 만족하는가'가 있다.
참조 지역성 원리란, CPU가 미래에 원하는 데이터를 예측하여 속도가 빠른 장치인 캐시 메모리에 담아 놓는데 이때의 예측률을 높이기 위하여 사용하는 원리이다. 최근에 참조한 메모리나 그 메모리와 인접한 메모리를 다시 참조할 확률이 높다는 이론을 기반으로 캐시 메모리에 담아놓는 것이다. 메모리를 연속으로 읽는 작업은 캐시 메모리에서 읽어오기에 빠른 반면, 무작위로 읽는 작업은 메인 메모리에서 읽어오기에 속도의 차이가 있다.
그렇기에 C는 상대적으로 다른 두 정렬들보다 큰 값으로 정의된다.
이와 달리, Merge sort의 경우 인접한 덩어리를 병합하기에 참조 지역성의 원리를 어느 정도 잘 만족한다. 그러나 입력 배열 크기만큼의 메모리를 추가로 사용한다는 단점이 있다.
(2) Tim sort
이 정렬 알고리즘은 Insertion sort와 Merge sort를 결합하여 만든 정렬이다.
실생활 데이터의 특성을 고려하여 더욱 빠르게 고안된 이 알고리즘은 최선의 시간 복잡도는 𝑂(n), 평균은 𝑂(𝑛log𝑛), 최악의 경우 시간 복잡도는 𝑂(𝑛log𝑛)이다.
Tim sort는 안정적인 두 정렬 방법을 결합했기에 안정적이며, 추가 메모리는 사용하지만 기존의 Merge sort에 비해 적은 추가 메모리를 사용하여 다른 O(nlogn) 정렬 알고리즘의 단점을 최대한 극복한 알고리즘이다
Tim sort 알고리즘은 Insertion sort와 Merge sort를 결합한 알고리즘이다. 여기에 시간 복잡도 O(N*N)으로 알려져 있는 Insertion sort를 왜 결합했을까?
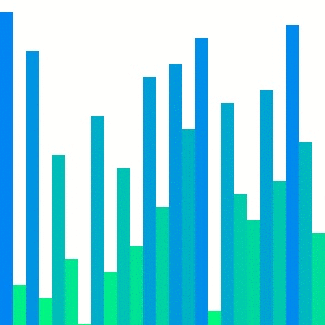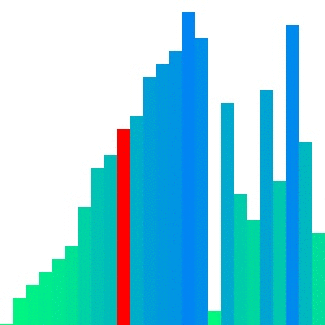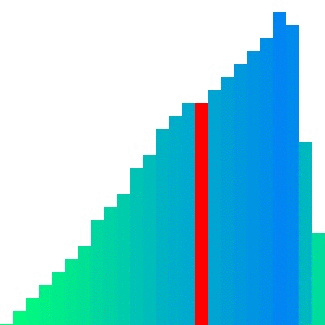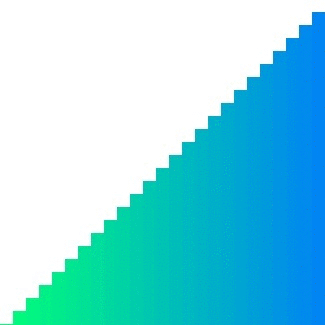
Insertion sort는 인접한 메모리의 비교를 반복한다. 참조 지역성의 원리를 매우 잘 만족하고 있는 것이다. 이것을 이용하여 전체를 작은 덩어리로 잘라 각각의 덩어리를 Insertion sort로 정렬한 뒤 병합하면 좀 더 빠르지 않을까 하는 것이 기본적인 아이디어이다.2^n개씩 잘라 각각을 Insertion sort로 정렬하면 일반적인 Merge sort보다 덩어리별 2^n개의 병합 동작이 생략된다.
Tim sort의 최적화 기법
1)Run
배열을 minrun(32~64)개씩 나눈다. 각 run내에서 binary insertion sort를 사용해 정렬한다. 그리고, 증가하거나 감소하는 연속된 요소들을 하나의 run으로 묶는다. 이렇게 정렬된 작은 묶음들을 더 큰 묶음으로 합친다. 비슷한 크기의 묶음끼리 합치는 게 효율적이다.
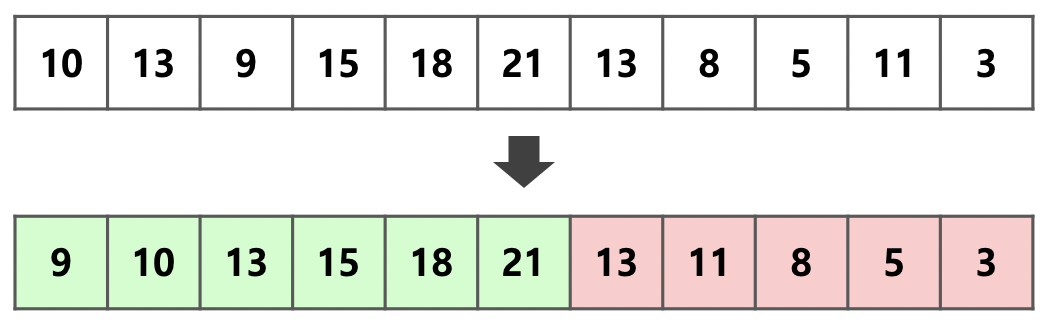
사실 이후의 내용은 아직 정확하게 이해하기가 어렵다. 더 공부를 해보자.
테스트
노션페이지에 팀소트와 버블소트를 비교한 것을 정리해두었다.
시간관계상 모든 알고리즘을 비교하진 못했는데, 추후에 비교해볼 계획이다.
https://awake-wealth-f67.notion.site/59fdb6100e5a44e09e7d963e19d2e403?pvs=4