팀원들과 처음 SeoulNolgoat을 구상했을 때는
가게 조합(1차 가게, 2차 가게, 3차 가게)들의 이동 동선을 먼저 확인하려고 했다.
1차 가게에서 2차 가게까지, 2차 가게에서 3차 가게까지
이동하는 데 걸리는 시간과 총 이동 거리를 확인해서
시간이 짧거나, 혹은 이동 거리가 적은 순서대로 정렬을 하려고 했다.
즉, 가장 이동 거리가 짧은 가게 조합(상위 10개정도)를 추천하려고 했다.
보행자 기준으로 이동 거리나 시간을 확인하려면 Tmap에서 제공하는 API를 사용해야 했다.
이용자가 1차, 2차, 3차 가게의 카테고리를 정하면
DB에서 해당 카테고리에 속하는 가게들은 100개씩 조회해야 한다.
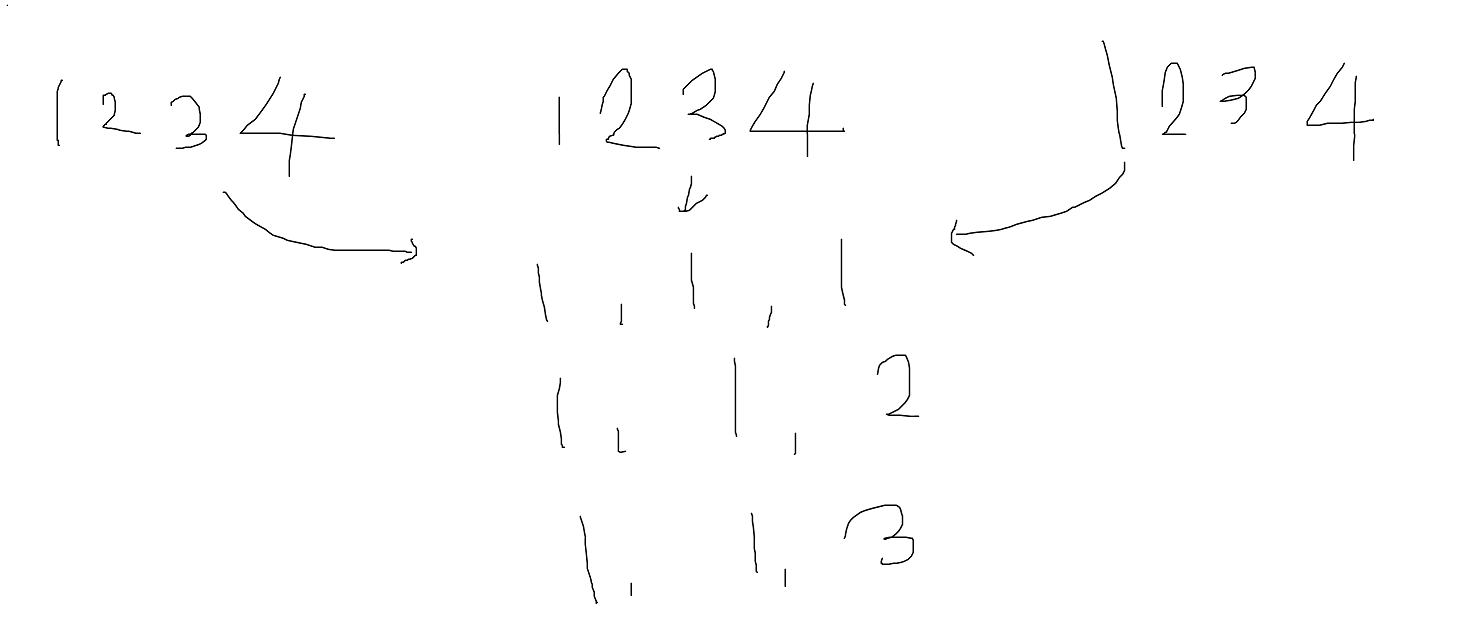
이런식으로 모든 조합을 만든 다음에Tmap API의 보행자경로 기능을 활용해서
모든 경우의 수에 대한 이동시간, 이동거리를 구하려고 했다.
API 호출을 해본 적이 없어서 몰랐는데 일정 횟수 이상을 사용하면 유료였다..!
100x100x100, 즉 100만건의 호출하는 건 애시당초에 불가능했다.
(이 방법은 성능에도 큰 영향을 주었을 거라고 생각한다.
Api 호출을 하면 네트워크로 정보를 받아와야 해서 시간이 오래 걸린다. DB보다 더 많이 시간이 걸리는 것으로 알고 있다.)
Tmap api가 호출 1000건까지만 무료라는 점을 생각하면 우리가 계획했던 대로 기능을 구현하는 것은 불가능하다.
효율적인 방식을 활용하자
팀원들끼리 얘기를 해서 새로운 방법을 고안해봤다.
1) 1차, 2차, 3차 가게들의 모든 조합을 구한다.
2) 현재 이용자 위치에서 1차->2차->3차의 직선 거리를 구하고 모두 더한다. 조합은 이렇게 더한 직선 거리들의 합이 작은 순서대로 정렬한다.
3) 2번에서 정렬을 끝낸 뒤, 상위 20개의 조합을 Tmap Api로 호출해서 보행자 기준 이동거리와 시간을 확인한다. 여기서 상위 10개의 조합을 보여준다.
(Tmap api에서는 경유지를 넣을 수 있어서 이를 활용하며 된다.)
직선 거리를 활용해야 한다는 점에서 정확도가 아쉽지만
가까운 것들을 추려내고 보정작업을 하는 것으로 기존 방식을 개선하기로 했다.
직선 거리 구하기
거리 구하기는 MySQL에서도 가능하고 스프링 서버에서도 가능하다.
작업을 DB와 스프링 서버에 적절하게 분배해줘야 한 곳에 부하가 쏠리는 것을 막을 수 있다. 일단 DB의 부하를 줄이는 것이 좋다고 생각해서 서버에서 이 작업을 하기로 했다.
참고 : 최단거리 구하기, 하버사인 공식(Haversine Formula)
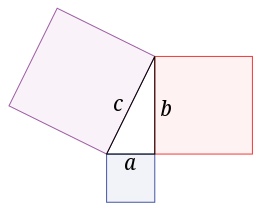
피타고라스의 정리에 따르면,
두 좌표 (x1, y1), (x2, y2)가 있을 때 두 지점 사이의 거리는 x좌표의 차이의 제곱과 y좌표의 차이의 제곱의 합에 대한 제곱근으로 구할 수 있다.
하지만, 이 방법을 쓸 수는 없다.
지구가 좌표평면에 있는 게 아니라 실제로는 둥글기 때문이다.
길이가 길어질 수록 지구 곡률에 의한 영향으로 거리에 왜곡이 생긴다.
두 지표점 사이의 거리는 3차원 공간 상에서 보면 직선이 아닌 호(Arc)의 모양이기 때문입니다. 가장 대표적인 예시로 비행기가 최단 거리로 가는 경로는 2차원 평면 도법 상의 직선거리가 아닌 비스듬한 거리입니다.
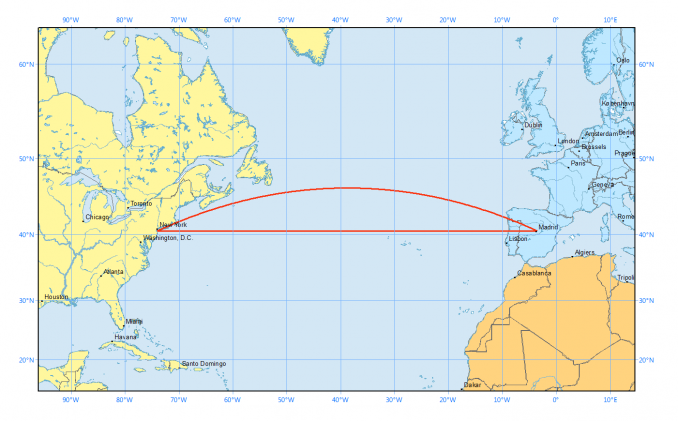
선의 길이는 직선이 더 짧지만 실제 거리는 원호로 표시된 경로가 더 짧습니다.
public class DistanceCalculator {
public static final double RADIUS = 6371; //지구 반지름(km)
public static final double TO_RADIAN = Math.PI / 180;
public static double calculateDistance(Coordination firstCoordination, Coordination secondCoordination) {
double firstLatitude = firstCoordination.getLatitude();
double firstLongitude = firstCoordination.getLongitude();
double secondLatitude = secondCoordination.getLatitude();
double secondLongitude = secondCoordination.getLongitude();
double deltaLatitude = Math.abs(firstLatitude - secondLatitude) * TO_RADIAN;
double deltaLongitude = Math.abs(firstLongitude - secondLongitude) * TO_RADIAN;
double sinDeltaLatitude = Math.sin(deltaLatitude / 2);
double sinDeltaLongitude = Math.sin(deltaLongitude / 2);
double squareRoot = Math.sqrt(
sinDeltaLatitude * sinDeltaLatitude +
Math.cos(firstLatitude * TO_RADIAN) *
Math.cos(secondLatitude * TO_RADIAN) *
sinDeltaLongitude * sinDeltaLongitude);
double distance = 2 * RADIUS * Math.asin(squareRoot);
return distance;
}이렇게 직선거리를 구할 수 있다.