버블 정렬
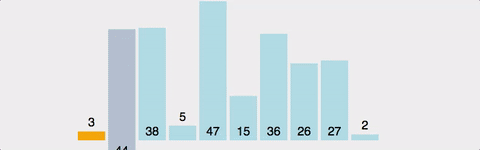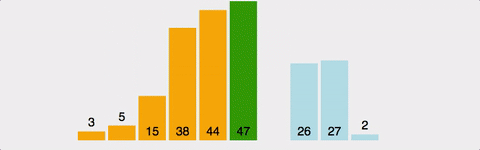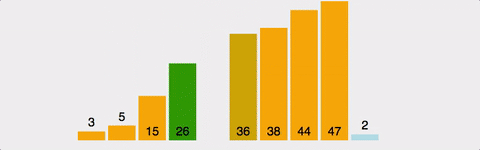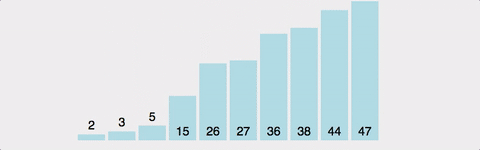
인접한 두 원소의 대소를 비교하고, 가장 큰 원소를 맨 뒤로 보낸다.
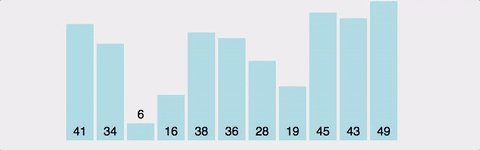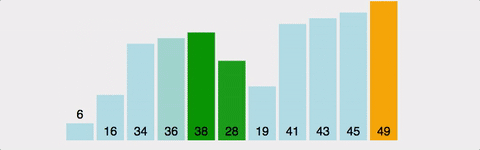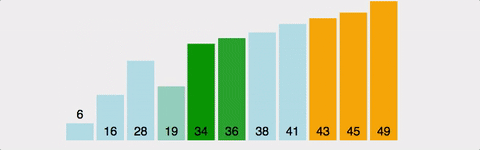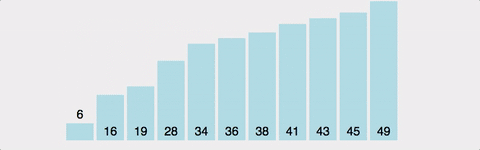
위 사진을 보면 1번의 있는 막대를 뒤로 옮기면서 계속 비교하고 움직이는 걸 볼 수 있다. 즉, 모든 막대마다 다 N번 비교를 해야 하므로, 시간 복잡도는 O(N^2)이다. 이건 최악의 경우만 그런 게 아니다. 정렬이 돼 있던 아니던, 2개의 원소를 계속 비교하기 때문에 최선/평균/최악 모두 O(N^2)이다.
공간 복잡도는 주어진 배열 안에서 교환이 되므로 O(N)이다.
선택 정렬
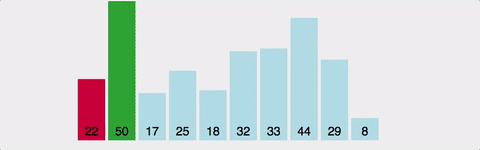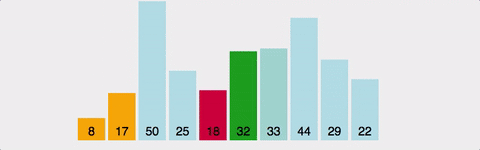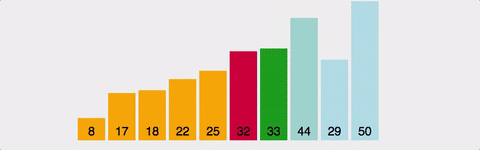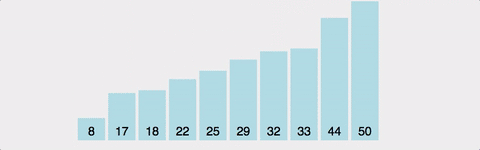
주어진 배열 중에서 최솟값읓 작고, 그 값을 맨 앞에 위치한 값과 변경한다. 이 과정을 반복하는 방식이다. 역시 O(N^2)의 시간 복잡도(최선/평균/최악)를 갖는다. 공간 복잡도는 O(N)이다.
버블 정렬에 비해서, 실제로 위치를 교환하는 횟수는 적기 때무넹 교환이 일어나야 하는 자료 상태에서는 비교적 효율적이다.
삽입 정렬
이미 앞에서부터 정렬을 해온 배열에서, 자신의 위치를 찾아 삽입하는 방식이다. 이미 정렬된 경우라면, 최선의 경우 O(N)의 효율성을 갖는다. 최악의 경우는 O(N^2)이다.
선택정렬과 삽입정렬의 차이는?
1) 선택 정렬은 가장 작은 것을 찾아서 맨 앞으로 가져오지만, 삽입 정렬은 현재 원소를 이미 정렬된 부분의 적절한 위치에 삽입한다.
2)선택 정렬은 안정적이지 않다(동일한 값의 원래 순서가 유지x), 삽입 정렬은 안정적이다(동일한 값의 원래 순서 유지)
3)선택 정렬은 항상 모든 비교를 수행하지만(정렬 상태와 무관), 삽입 정렬은 이미 정렬된 배열에서는 O(n)의 시간 복자도다.
4)선택 정렬은 매번 전체 배열을 탐색하지만, 삽입 정렬은 적절한 위치를 찾고서 탐색을 종료할 수 있다.
퀵 정렬
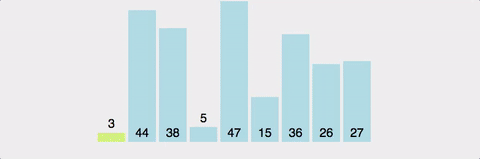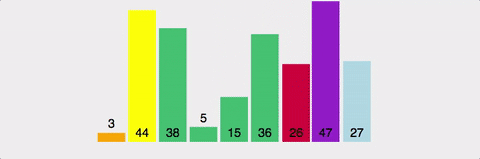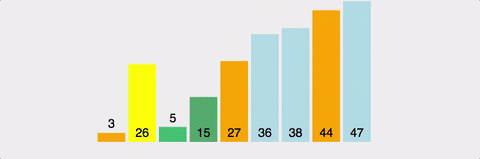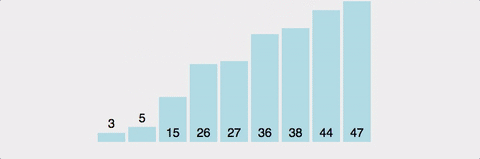
분할 정복으로 배열을 정렬한다.
배열에서 피벗을 고르고, 피벗앞에는 피벗보다 작은 값이 오고 뒤에는 큰 값이 온다.
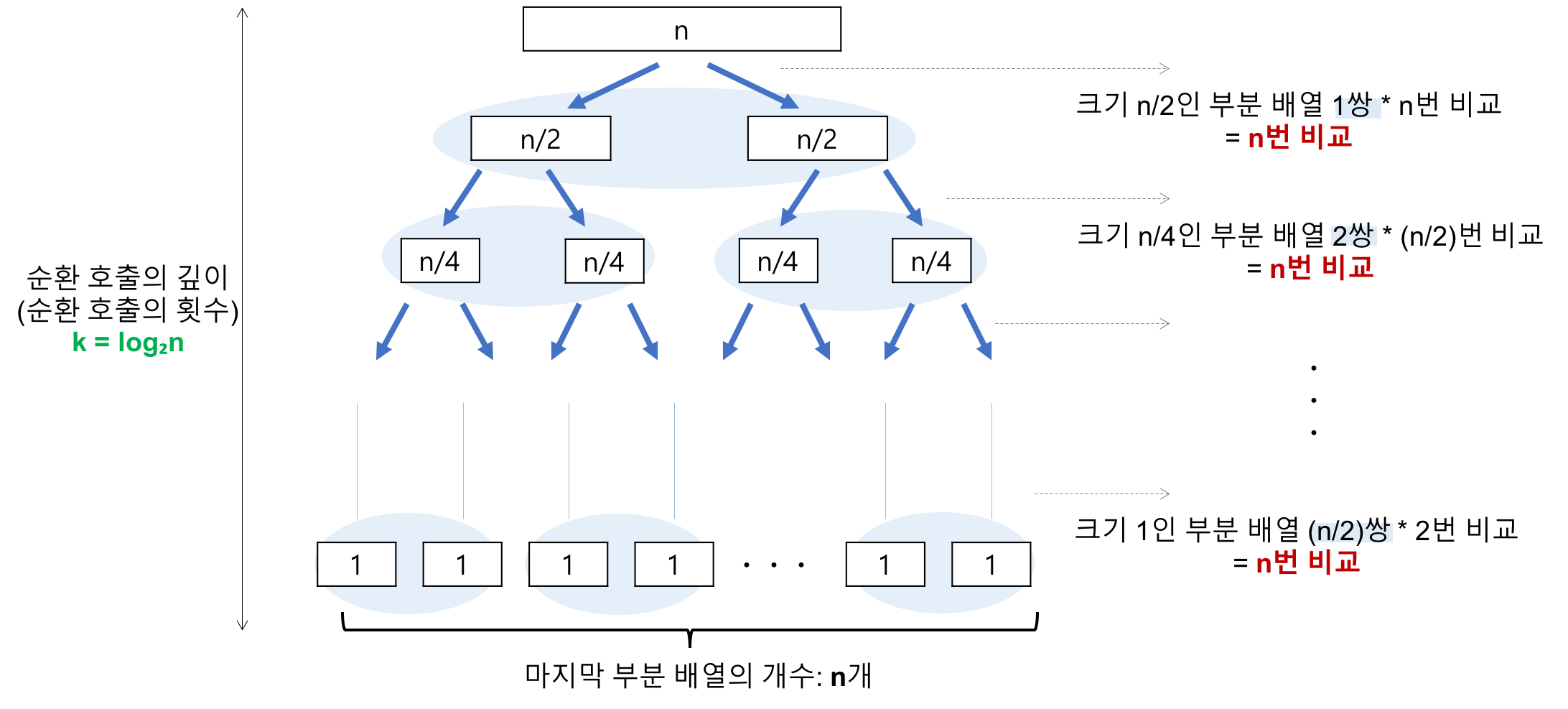
최선의 경우 시간 복잡도는 O(nlog2n)이다. 각 단계마다 연산은 N번 발생하는데, 전체 깊이는 log2N이다.
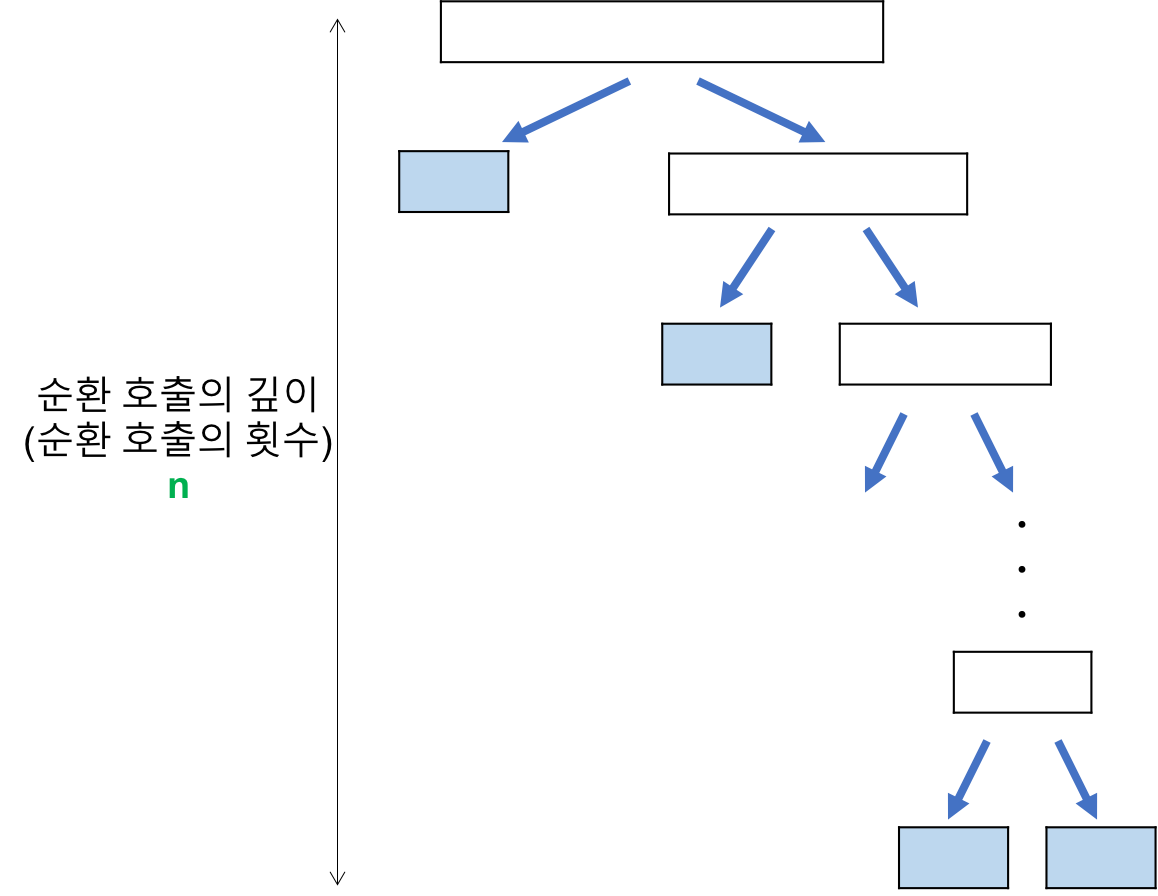
최악의 경우는 O(N^2)이다. 정렬하고자 하는 배열이 오름차순 or 내림차순으로 정렬된 경우다.
합병 정렬
[참고자료]