ANOVA 분산분석(일원,이원)

📌 ANOVA

• 세 개 이상의 모집단이 있을 경우에 여러 집단 사이의 평균을 비교하는 검정방법
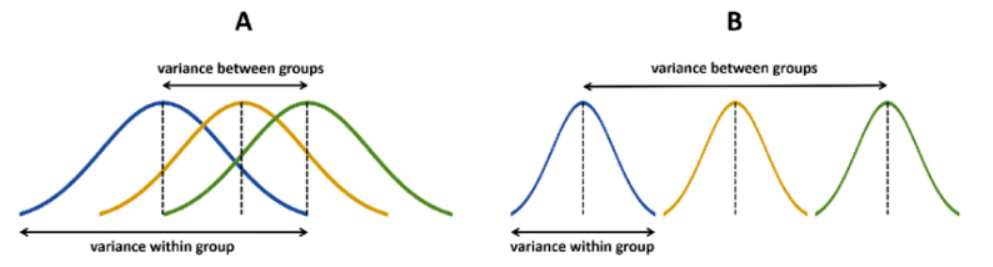
• 분산분석이라는 용어는 분산이 발생한 과정을 분석하여 요인에 의한 분산과 요인을 통해 나누어진 각 집단 내의 분산으로 나누고 요인에 의한 분산이 의미 있는 크기를 가지는지를 검정하는 것을 의미한다.(F-value=그룹 간 분산 / 그룹 내 분산)
• 독립변수는 범주형 변수이어야 하며, 종속변수는 연속형 변수이어야 한다.
  
  A그림은 그룹 사이에 차이가 없다.
  B그림은 그룹 사이에 차이가 있다라고 볼 수 있다.

📖 ANOVA 분산분석의 사용 이유

집단 수가 늘어날수록 t-test검정을 반복적으로 수행하면 1종 오류가 증가하게 되는데, 이 1종 오류를 줄이기 위해 집단 수가 늘어날수록 ANOVA 분산분석을 사용한다.

📖 분산분석의 전제조건

• 독립성 : 각 집단은 서로 독립이어야 한다. (상관관계로 확인)
• 정규성 : 각 집단은 정규분포를 따라야 하며 정규성 검정의 종류는
  Q-Q plot, Shapiro, Kolmogorov-Smirnov가 있다.
• 불편성(등분산성) : 각 집단의 평균은 달라도 분산은 같아야 한다.

📖 일원분산분석

일원분산분석 : 서로 독립인 세 집단의 평균 차이를 검정

셋 이상의 집단 간 평균을 비교하는 상황에서 하나의 집단에 속하는 독립변수와 종속변수 모두 한 개일 때 사용

ex) 강남구에 있는 GS편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 있는가?        라는 물음에 대해
귀무가설 : GS편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 없다.
대립가설 : GS편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 있다.
라는 가설을 설정할 수 있다.

정규성 검정을 위해 : stats.shapiro(변수명).pvalue
등분산성 검정을 위해 : 
stats.levene(변수명들).pvalue   --> 모집단이 많을 때 levene(비모수적)
stats.bartlett(변수명들).pvalue --> 모집단이 적을 때bartlett(모수적)
일원분산분석 방법 : stats.f_oneway(변수명들)
이때 pvalue값이 0.05보다 작다면 대립가설을 채택하게 된다.

분산분석표 보기 : anova_lm(model)

📖 이원분산분석

두 개의 요인에 대한 집단(독립변수) 각각이 종속변수의 평균에 영향을 주는지 검정이다.

💡이때 가설검정은 주효과 2개, 교호작용 1개로 총 3번한다.(독립2개, 종속1개인 경우)

• 주효과 : 독립변수들이 각각 독립적으로 종속변수에 미치는 영향을 검정
• 교호작용 : 한 요인의 효과가 다른 요인의 수준에 의존하는 경우
  (상승효과-효과가 더 좋아짐, 상쇄효과-효과가 더 떨어짐)
  독립변수2개가 종속변수 1개를 설명하는데 도움이 된다면 교호작용이 있다고 판단한다.
  ex. 초밥에 간장 - 상승효과, 초밥에 케찹 - 상쇄효과

  ---

  poison과 treat가 독퍼짐 시간의 평균에 영향을 주는가?
                              라는 질문에서
  <주효과 가설>
  귀무가설 : poison 종류와 독퍼짐 시간의 평균에 차이가 없다. 대립가설 : poison 종류와 독퍼짐 시간의 평균에 차이가 있다. 귀무가설 : treat(응급처치) 방법과 독퍼짐 시간의 평균에 차이가 없다. 대립가설 : treat(응급처치) 방법과 독퍼짐 시간의 평균에 차이가 있다.

  ---

  <교호작용 가설>
  귀무가설 : 교호작용이 없다.(poison 종류와 treat(응급처치)방법은 관련이 없다.) 대립가설 : 교호작용이 없다.(poison 종류와 treat(응급처치)방법은 관련이 있다.)

분산분석표 보기 : anova_lm(model)
상호작용을 보기1 : C(변수1):C(변수2)
상호작용을 보기2 : C(변수1)*C(변수2)

📖 사후분석

• ANOVA 검증 결과 유의미하다는 결론을 얻었을 때, 구체적으로 어떤 수준에서 평균 차이가 나는지를 검증하는 방법
• 방법 : 검정방법이 존재하나 Tukey, Duncan, Scheffe를 주로 사용
  ex)

from statsmodels.stats.multicomp import pairwise_tukeyhsd
tkResult = pairwise_tukeyhsd(endog=종속변수, groups=독립변수)
print(tkResult)

정리

• 요인이 한개가 여러개로 나뉘면 일원분산분석
  (ex. 매장위치 - 강남,강동,강서,강북..) -> 만족도(종속) or 정해진 시점(참여 전,1달후,2달후) -> 성적
  
  
• 요인이 두개면 이원분산분석
  (ex. 온도(1000도,1500도), 기계(오븐,기름) -> 맛(종속) or 집단(실험군,대조군), 시점(시험전,후) -> 통증
• Tukey와 Duncan은 집단의 수가 같을 때 사용하는 방법
• Scheffe은 집단의 수가 다를 때 사용하는 방법