통계 한짤 요약

통계 파트는 지금까지의 수업과는 다르게 실습없이 이론만 듣는 파트라서 커피를 3잔을 먹은 거 같다.. ㅎㅎ
EDA(Exploratory Data Analysis)
EDA를 전처리라고 만 알고있었으나 이번장에서 풀네임을 알게 되었다.
도표, 그래프, 요약 통계 등을 사용하여 데이터를 체계적으로 분석하는 방법
프로젝트 초기에 가설을 수립하고 적절한 모델/기법을 선정하기 위해 사용
변수 간 트렌드, 패턴, 관계 등을 찾고 통계적 추론을 기반으로 가정을 평가
분석 데이터에 적절한지 평가하고 추가 수집, 이상치 발견 등에 활용
데이터 시각화(Data Visualization)
시간 시각화 : 막대 그래프, 누적 막대 그래프, 점 그래프
분포 시각화 : 파이 차트, 도넛 아트, 트리맵, 누적 연속 그래프
관계 시각화 : 스캐터플롯, 버플차트, 히스토그램
비교 시각화 : 히트맵, 스타 차트, 평행 좌표계, 다차원 턱도법
공간 시각화 : 지도 맵핑
EDA 파트에서 했던 것들이 나온다.
기초 통계량
평균
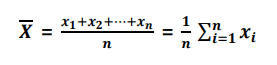
중앙값
이상치가 존재 할때 평균의 신뢰도가 떨어져 중앙값을 사용하게 된다고 한다.

최빈값
가장 빈번하게 나오는 값을 의미 한다.
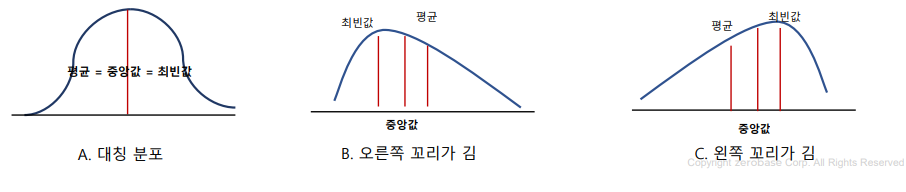
분산
데이터의 분포가 얼마나 흩어져 있는지를 알 수 있는 측도
표준편차
분산의 제곱근으로 정의함
변동계수
평균이 다른 서로 다른 그룹을 비교할때 표준편차를 비교할 때 사용한다
실제 분석에서 자주 사용한다고함
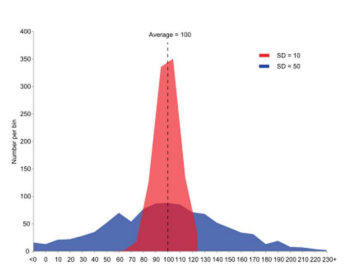
분산이 크면 분포가 넓어지고 분산이 작으면 분포가 좁아지는 대신 평균이 높아진다.
확률
확률(Probability) : 모든 경우의 수에 대해 특정 사건이 발생하는 비율
표본 공간(Sample Space) : 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합EX) 동전 던지기 S = {앞면, 뒷면}, 주사위던지기 S = {1,2,3,4,5,6}
통계적 확률
어떤 시행을 N번 반복했을 때, 사건 A가 r번 일어난 경우 r/N이고, 이를 사건 A가 발생할 상대도수라고 함
N이 무한히 커지면 상대도수는 일정한 수로 수렴함
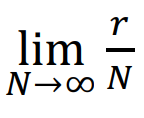
EX) 타자가 타석에서 안타를 칠 확률, 공정에서 제품이 정상일 확률(수율)
조건부 확률(conditional probability) : 어떤 사건 A가 발생한 상황에서또 하나의 사건 B가 발생할 확률

확률변수
확률 변수(random variable): 표본공간에서 각 사건에 실수를 대응시키는 함수를 확률 변수라고 한다.
일반적으로 대문자 알파벳으로 표시한다.
EX)
(a) 반도체 1000개의 wafer중 불량품의 수 X
(b) 공장에서 생산하는 전구의 수명 T
(c) 주사위를 던질 때 나오는 눈의 수
확률 변수 평균 기댓값이라고도 표현한다.
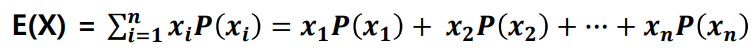
기댓값의 성질

분산의 성질

이산 확률 분포
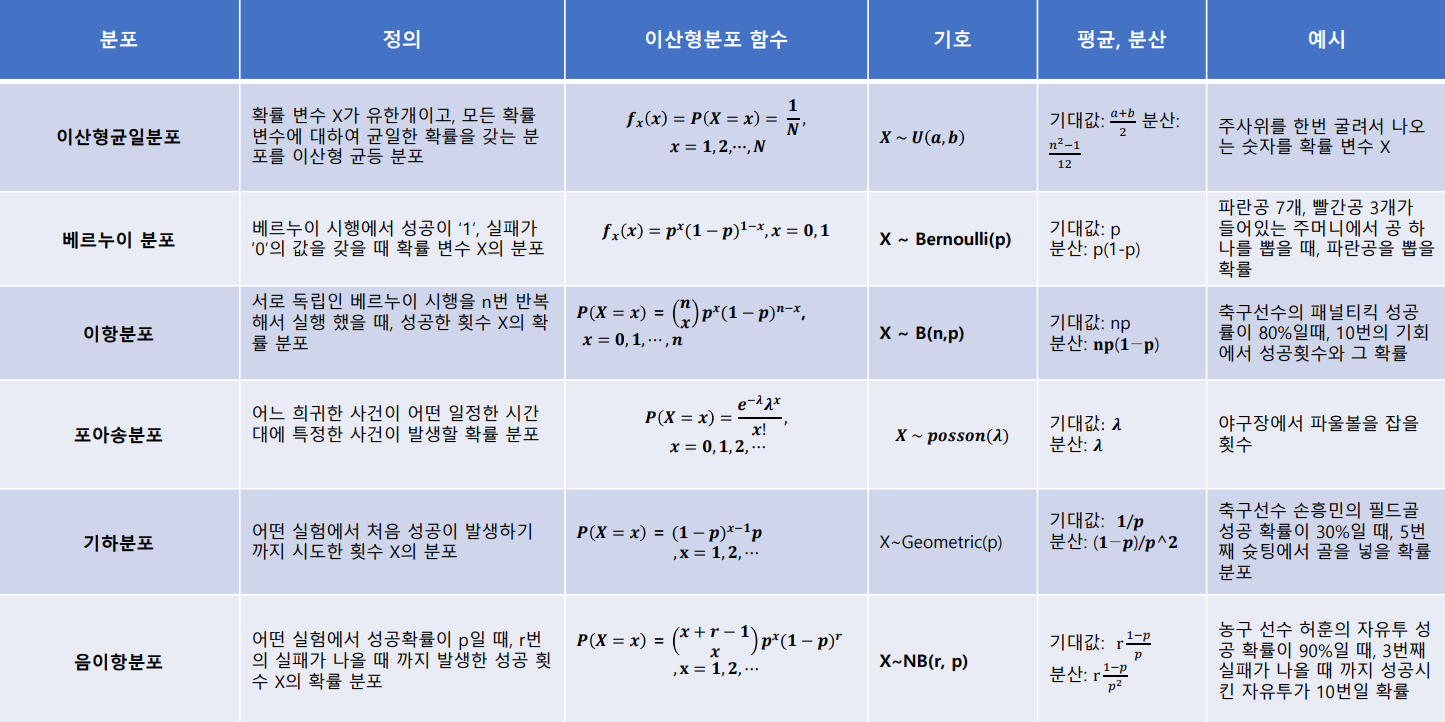
어떤 분포를 사용해야하는지를 외우는 것을 중심으로 해야할것 같다.
