[알고리즘] LCS ( Longest Common SubSequence)

한호성·2022년 6월 8일

알고리즘

LCS (최장 공통 수열)

개념

가장 긴 공통된 부분수열을 구하는 문제이다. 임이의 두 수열에서 각각의 부분 수열들 중 서로 같은 부분 수열을 의미한다.

백준 9251번 예시 를 보자

두 문자열 ACAYKP , CAPCAK 가 주어지고, LCS 는 ACAK이다. 이것을 어떻게 구할 것인가...

동적계획법( Dynamic programming) 을 통해서 푸는 과정을 설명해보자..

LCS문제의 겨우 부분수열에서 '순서'가 지켜지는 것이 포인트이다.

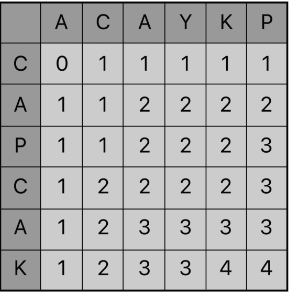
다음 표를 확인해보자.

다음 표를 채우는 기준은 다음과 같다.

각 가로 세로 문자까지의 수열들 중 LCS 공통 수열의 길이를 채택하는 것이다.

예를들어 (1,2)= (A,A) 를 생각해보자 'CAPCAK' 중 {C,A} 'ACAYKP' 중 { A,C,A} 의 중 겹치는 수열의 개수를 나타내는 것이다. 즉 2이다 {C,A}

이런 방식으로 표를 채우면 위 사진과 같아진다.

이 표를 확인해보면 다음과 같은 점화식을 세울수 있다..
x번째 원소와 y번째 원소가 같다면 (x-1,y-1)의 lcs길이의 +1 이된다.
만약 다르다면, Lcs ( x(i-1) y(j) ) 값 혹은 lcs (x(i),y(j-1))값들중 큰 값이 오면 된다.

LCS(Xi,Yi) : ( LCS( X(i-1) ,Y(j-1) ) +1 ) if(xi==yj)
LCS(Xi,Yi) : max( LCS(X(i-1), y(j) , LCS(X(i), y(j-1) ) if(xi!=yj)

~~( 도대체 이런 표랑 점화식 같은건 어떻게 찾을수 있는 건가.. ㅋㅋ ) 이렇게 완성된걸 보면 이해는 되는데. 처음 문제를보면 떠오르질 않는걸..~~

알고리즘 코드구현

Top-Down 방식의 재귀형식으로 코드를 작성하면 다음과 같다.

static int LCS(int x ,int y ){


//인덱스가 0,0 재귀호출을 통해 x,y값이 -1 값들어오면 0으로 return해줘야함.
  if(x==-1|| y==-1){
      return 0;
  }
  if(dp[x][y]==null){
  	dp[x][y]=0;
    
    //문자가 같은지 검사 점화식대로 코드작성하면된다.
    if(str1[x]==str2[y]){
    	dp[x][y]=LCS(x-1,y-1)+1;
    }
    //다르다면
    else{
    	dp[x][y] = Math.max(LCS(x - 1, y), LCS(x, y - 1));
    }
  }
  
  return dp[x][y];
  
}