냅색 알고리즘

개념

백준 12865번 문제 https://www.acmicpc.net/problem/12865

배낭문제로 유명한 냅색 알고리즘이란 것이 있다고 한다. 처음 들었다.

배낭문제, 일명 냅색 알고리즘은 2가지 분류된다.
[1] 짐을 쪼갤 수 있는 경우
[2] 짐을 쪼갤 수 없는 경우

두 경우에 따라 다름 알고리즘을 적용한다고 한다.

[1] 경우 : 탐욕 알고리즘(Greedy)를 쓴다.
[2] 경우 : DP(Dynamic programming) 을 쓴다.

현재 주어진 문제는 짐을 쪼개지 않는 문제기 때문에 DP를 통해 문제를 해결한다.

풀이 접근

1차원 배열 두개(W[] =주어진 무게 ,V[]= 주어진 가치)
2차원 배열 DP[i][K] = maxValue

dp 이차원 배열에 대한 이해가 중요하다 행은 i 번째 물건까지 탐색했을 경우를 의미한다.
dp 열은 포함가능한 최대 무게를 의미한다.

아래 표를 한번 확인해보자

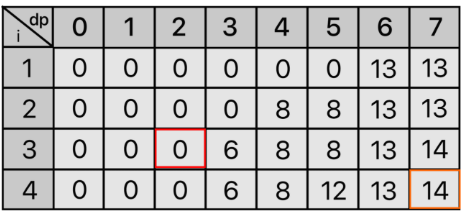
아래 표를 채우는 방식은 다음과 같다. i 번째, 무게 K까지 수용가능한 최대 가치를 구하기 위해서는
1. i번째 물건이 최대 무게 k값보다 작은지 확인하고 최대 무게 값보다 크다면 i-1까지 탐색한 값을 대입한다.

2. 1번 조건을 통과할 경우 , dp[i-1][k] 값과 ( V[i] + dp[i-1]k-W[i]] ) 을 비교해 큰 것을 대입한다.

3. i==0 || k==0 일 때 0 대입 (즉 최대무게 0 , 물건의개수 0) 일 경우 당연히 영이다.

점화식을 나타내면 다음과 같다.

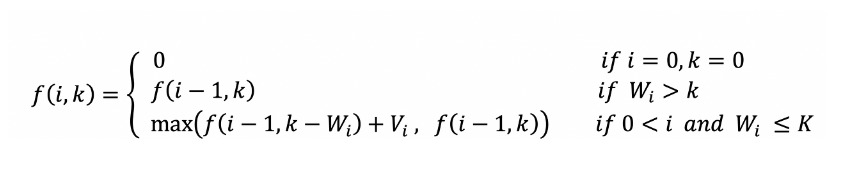
풀이 코드

Top-down 방식으로 나타내면

	static int knapsack(int i , int k){
    	
        // 물건이 0번째와 비교해야할 경우 즉 물건이 없을 경우는 당연히 0을 return 해야지
        if(i<0){
        return 0; 
        }
        
        //탐색하지 않은 배열일 경우
        if(dp[i][k]==null){
        	//주어진 최대무게보다 물건의 무게가 크면 이전의 값이 최대가치의 값이다.
            if(W[i]>k){
            	dp[i-1][k];
            }
            //적재 가능한 무게일 경우 점화식대로 표현
            //현재 적재한 무게의 가치 + 현재 적재한 무게를 빼고 이전까지 탐색한 물건들 중에 적재할 수 있는 최대 가치 와 이전물건까지의 탐색 가치를 비교해서 큰 것을 대입
            else{
            	Math.max( knapsack([i-1][k]), V[i]+ Knapsack(i-1 , K-W[i]));
		
            }
        }
        return dp[i][k];
    }

bottom up 방식

for(int i=1 ; i<=N;i++){

// K부터 탐색하여 담을 수 있는 무게 한계치가 넘지 않을 때까지 반복
	for(int j=K ; j-W[i]>=0;j--){
    
    	dp[j] = Math.max(dp[j],dp[j-W[i]] +value[i]);
    
    }
}

Reference

https://st-lab.tistory.com/141