[알고리즘]-정렬 (Merge sort)

한호성·2022년 5월 20일

Merge sort (합병정렬)

개념

문제를 분할하고, 분할한 문제를 정복하여 합치는 과정이다. 정렬해야 할 리스트가 주어지면, 해당 리스트를 분할을 반복하여, 최대한 작게 쪼개진 시점에 부분리스트에서 원소간 비교를 통해 정렬한다.

합병정렬은 비교정렬이며, 안정정렬이다.

정렬방법

1. 주어진 리스트를 절반으로 분할하여 부분리스트로 나눈다. (Divide : 분할)

2. 해당 부분리스트의 길이가 1이 아니라면 1번 과정을 되풀이한다.

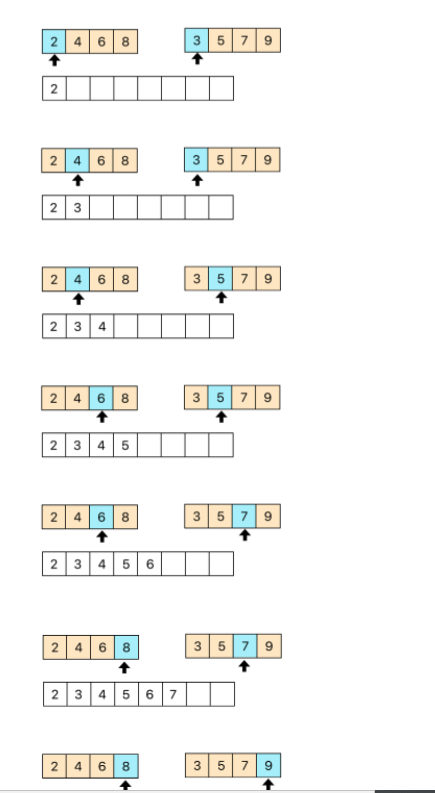
3. 인접한 부분리스트끼리 정렬하여 합친다. (Conqure : 정복)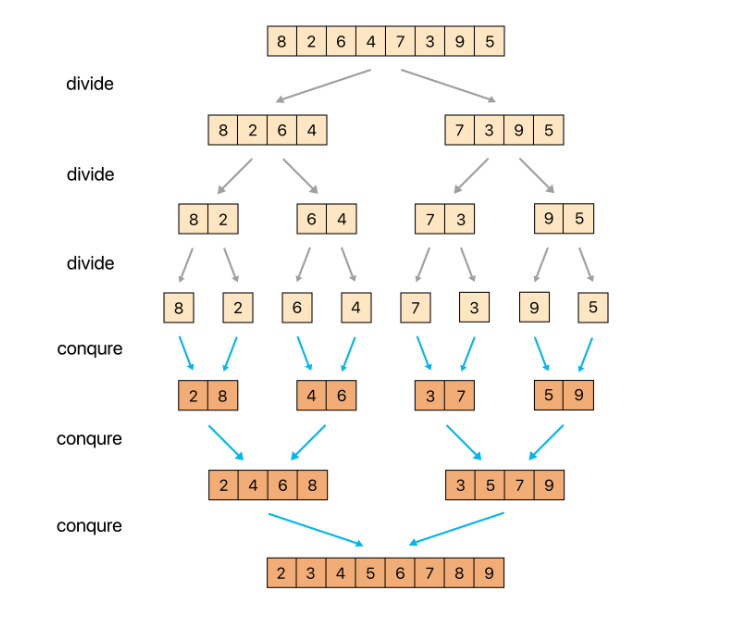

각 부분리스트를 합쳐서 정렬할 때 정렬하는 방법 이미지를 통해 확인하자

코드 구현

public class Merge_sort_myOwn {

    private static int [] sorted;

    public static void main(String[] args){

        int [] merge_array = { 2,1};
        merge(merge_array);
        for(int i=0; i<merge_array.length;i++){
            System.out.print(merge_array[i]+" ");
        }
    }

    public static void merge(int [] a){

        sorted = new int[a.length];
        merge(a,a.length);
        //garbage collector 에 의해 정리되게 하기 위해서
        sorted=null;
    }

    private static void merge(int [] a ,int length){


        //bottom up 방식으로 하자
        int left=0;
        int right ;
        int mid;

        //size 1-2-4-8 로 시작
        for(int size=1 ;size<length;size+=size){

            for(left =0; left< length-size ;left+=size*2){

                int low = left;
                mid  = left+size-1;
                right = Math.min(left + (size*2)-1, length-1);
                System.out.println( "low :"+ low + " mid : "+ mid + " right :"+ right );
                merge_sort(a,low,mid,right);

            }
        }
    }

    private static void merge_sort(int [] a,int left ,int mid, int right ){

        int l = left;
        int r = mid+1;
        int idx =left;
        while(l<=mid && r<=right){

            // 왼쪽이 더 작을 경우
            if(a[l]<=a[r]){
                sorted[idx]=a[l];
                l++;
                idx++;
            }
            //오른쪽이 더 작을 경우
            else{

                sorted[idx]=a[r];
                r++;
                idx++;
            }
        }

        //오른쪽이 들어가고, 다른한쪽이 남았을 경우
        if(l<=mid){
            while(l<=mid){
                sorted[idx]=a[l];
                l++;
                idx++;
            }
        }
        //왼쪽이 들어가고, 다른 한쪽이 남았을경우
        else{
            while(r<=right){
                sorted[idx]=a[r];
                r++;
                idx++;
            }
        }

        for(int i=left ; i<=right;i++){
            a[i]=sorted[i];
        }
    }

}