[알고리즘] 정렬- Heap sort

한호성·2022년 5월 18일

알고리즘

Heap Sort (힙 정렬)

Heap 자료구조

Heap( Using array)
힙은 '최소값 또는 최대값을 빠르게 찾아내기 위해 완전이진트리 형태로 만들어진 자료구조'다
Keywords : 최솟값,최대값, 빠르게,완전이진트리

완전이진트리

일반적인 트리구조

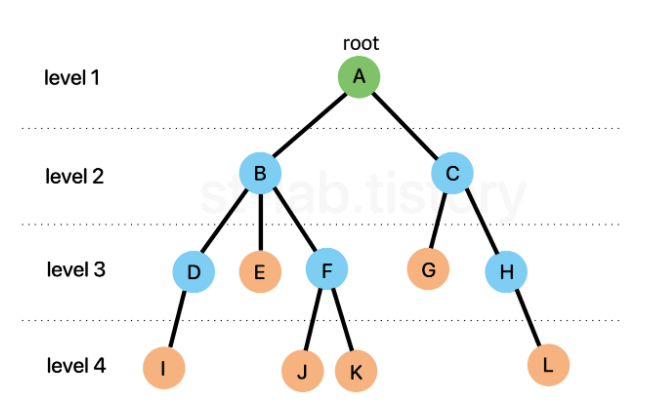
트리구조에 사용되는 용어

부모노드 (parent node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 높은 노드를 의미 (ex. F의 부모노드 : B)
자식노드 (child node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 낮은 노드를 의미 (ex. C의 자식노드 : G, H)
루트노드 (Root node) : 일명 뿌리 노드라고 하며 루트 노드는 하나의 트리에선 하나밖에 존재하지 않고, 부모노드가 없다. 위 이미지에선 녹색이 뿌리노드다.
단말노드 (Leaf node) : 리프 노드라고도 불리며 자식 노드가 없는 노드를 의미한다. 위 이미지에서 주황색 노드가 단말노드다.
깊이 (Depth) : 특정 노드에 도달하기 위해 거쳐가야 하는 '간선의 개수'를 의미 (ex. F의 깊이 : A→B→F 이므로 깊이는 2가 됨)
레벨 (level) : 특정 깊이에 있는 노드들의 집합을 말하며, 구현하는 사람에 따라 0 또는 1부터 시작한다. (ex. D, E, F, G, H)
차수 (degree) : 특정 노드가 하위(자식) 노드와 연결 된 개수 (ex. B의 차수 = 3 {D, E, F} )

완전이진트리구조
: 마지막 레벨을 제외한 모든 노드가 채워져 있으면서, 마지막 레벨의 노드가 왼쪽부터 채워져 있어야 한다.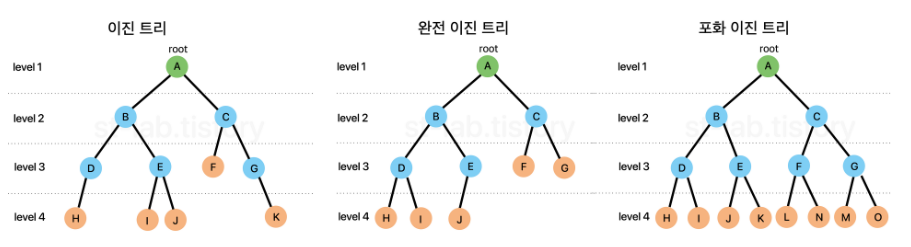

*cf) 형제간 우선순위는 고려하지 않는다. -> 이 상태를 반 정렬 상태, 약한 힙 이라고 부른다

이진트리 성질

1. 왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2 
2. 오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2 + 1
3. 부모 노드 인덱스 = 자식 노드 인덱스 / 2

힙 자료구조의 add/ remove

알고리즘 구현

[과정 1] : 최대 힙 만들기

핵심
- 가장 첫 번째로 검사하는 노드는 `가장 마지막 노드의 부모 노드 서브트리`
- 변경 후 , 하위 서브트리 다시 재검사

[과정 2] : 정렬하기
- 최대힙으로 정리된 0번 원소를 가장 마지막 원소와 바꾸고, 마지막 원소를 제외한 배열간의 최대힙으로 변경
- 다시 쵀대힙으로 정리된 0번 원소와 마지막 원소-1 위치와 바꾸고  마지막원소 -1 까지 빼고 최대힙으로 변경

이 과정 반복 (전체길이 -1) 후 배열 출력 -> 오름차순

알고리즘 코드 구현

public class HeapSort {

    //오름차순 정렬
    //과정 1. 최대힙 만들기 (heapify)
    //과정 2. 정렬하기

    public static int[] a ={4,5,6,1,2,3};

    public static void heapSort(){
        //마지막 인덱스
        int arr_length = a.length;

        //부모인덱스
        int parentIdx= (a.length-2)/2;

        //과정 1. 최디햅 만들기
        for(int i =parentIdx ; i>=0;i--){
            heapify(i,a.length-1);
        }

        //과정 2. 정렬하기

        for(int i =a.length-1;i>0;i--){
            int temp = a[0];
            a[0]=a[i];
            a[i]=temp;
            heapify(0,i-1);
        }
    }

    private static void heapify(int parentIdx, int lastIdx){


        while( (parentIdx*2)+1 <=lastIdx){

            int leftChildIdx=parentIdx *2 +1 ;
            int rightChildIdx= parentIdx *2+2 ;
            int largestIdx = parentIdx;


            if( leftChildIdx<=lastIdx && a[leftChildIdx]< a[largestIdx] ){
                largestIdx=leftChildIdx;
            }
            if( rightChildIdx<=lastIdx && a[rightChildIdx]< a[largestIdx] ){
                largestIdx=rightChildIdx;
            }

            //큰 idx가 변했다는 의미.
            if(parentIdx!=largestIdx){
                int temp = a[largestIdx];
                a[largestIdx]=a[parentIdx];
                a[parentIdx]=temp;
                parentIdx=largestIdx;
            }
            else{
                return;
            }
        }
    }
    public static void main(String[] args){

        heapSort();
        for(int i=0;i<a.length;i++){
            System.out.print(a[i] + " ");
        }
    }
}

힙 정렬의 장단점

안정적인 성능
- 하나의 노드를 삽입하거나 삭제했을 때 규칙을 유지하도록 바꾸는 작업은 O(log n)이다. 이진 트리의 높이만큼 반복하기 떄문
- 힙정렬의 경우 최악의 경우 n 개 숫자를 삽입/삭제 해야한다. 시간복잡도는 O(n logn) 이다. -> 괜찮은 시간복잡도
추가 메모리 공간 필요 없음
- 힙 정렬은 배열 안에서 계속 요소의 위치를 바꾸는 식으로 힙 구조를 유지하므로 추가 공간이 필요 없다.
일부분만 필요할 때 좋음
- 전체 숫자 중에서 가장 작은 숫자 k개 를 구해라 이런 문제에 적합, 전체적인 정렬을 하지 않고 ,가장 작은 k 개의 값만 구하면 된다.