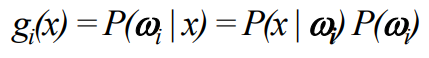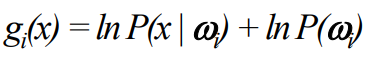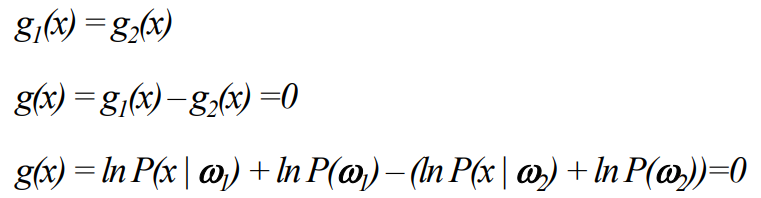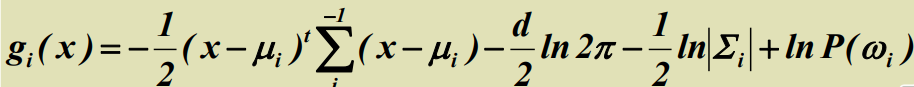✍ Parameter Estimation
대학교에서 들은 ML course의 정리
생성 모델과 판별모델
생성 모델 (generative)
생성 모델은 확률분포 모형을 결과값(output)으로 나타낸다. 확률 분포를 결과값으로 나타냄으로
N(μ, σ^2)
으로 나타낼 수 있다. 이때 μ는 평균을 나타내고, σ는 표준편차를 나타낸다.
판별 모델 (Discriminative)
판별 모델을 판별식을 찾는 것을 목적으로 하는 모델이다
Parametric vs Non - parametric
<Parametric>
사전에 정의된 매개변수를 모델에 사용하는 것을 말한다. 생성모델의 경우 매개변수는 평균과 표준편차이다.
<Non-parametric>
매개변수가 모델에 없는 것
Decision Boundary의 판별 함수
각 클래스는
로 판별 함수를 나타낼 수 있다. 이것을 활용하기 편하게 하기 위해서 양쪽에 자연로그를 씌운다.
로그를 취해도 로그는 단조 증가임으로 값의 scale에는 변동이 없다. 따라서 순서가 바뀌는 일이 일어나지 않는다.
이것을 이용하여 Decision Boundary를 나타내면 다음과 같다.
Gaussian 분포
관측된 데이터 (N(μ, σ^2))에 대해서 유일한 확률 함수는 class-conditional이다.
Univariate 와 multivariate Gaussian
Univariate인 경우 하나의 확률 분포에 대해 나타내고 multivariate은 여러개의 확률분포를 통해 나타낸 gaussian 분포이다.
Univariate
Multivariate
판별 함수를 Gaussian에 적용
판별 함수 (g(x))를 Gaussian (P(x))에 적용하면 다음과 같다.
Maximum Likelihood 측정
가우시안의 분포의 매개변수는 앞서 설명한대로 두가지가 존재한다.
평균 백터 : μ
공분산 행렬 : Σ
이때, 확률 함수에서 가장 큰 값을 뽑아오는 매개변수를 Maximum likelihood라고 칭한다.
generative and parametric approach
매개변수는 고정된 추측이 가능하지만 모를 수 있다. 가장 좋은 매개변수는 관측된 예시들을 통해 확률의 최대치를 뽑아오는 매개변수가 가장 좋은 매개변수이다. 만약 샘플의 크기가 증가하면 예측값은 더 좋은 값으로 수렴한다.
전체 학습 데이터 D가 n개의 샘플들을 갖고 있다고 하자
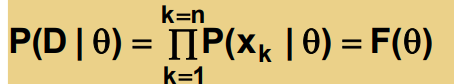
이때 θ의 값은 학습 데이터에서 가장 fit한 값을 나타낸다.
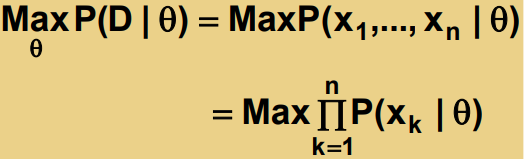
log-likelihood
P(D|θ)를 쉽게 계산하기 위해 자연 로그 ln을 씌운다.
l(θ) = ln P(D|θ) 를 나타내면 다음과 같다.
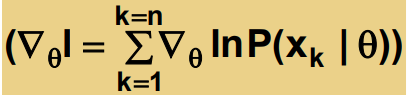
특수한 경우: unknown μ (또는 Σ)
평균을 모르는 경우 최대 likelihood를 구하는 방법은 다음과 같다.
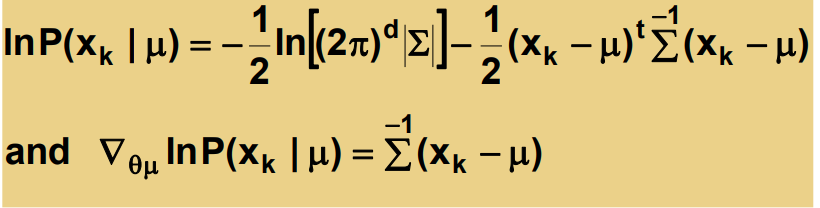
여기서 생략된 식 (-1/2ln[...])은 상수임으로 생략이 가능하다.
이것을 통해 알수 없는 μ (또는 Σ)을 모델에서 예측할 수 있다.
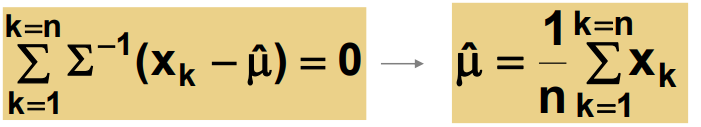
여기서 나온 추측된 μ (또는 Σ) 값은 산술평균의 형태를 띄는 것을 확인할 수 있다.
특수한 경우: unknown μ and σ
두 매개변수를 모르는 경우 가장 fit한 값을 갖고 있는 θ을 사용하여 두 매개변수를 추측한다.

이것을 이용하여 매개변수를 추축하는 수식은 다음과 같다.

이것을 n개의 샘플에 대한 덧샘을 이용하면 두 매개변수를 추측한 값이 나온다.

Naive Bayesian classifier
더 높은 차원에서의 θ값을 추측하긴 너무 복잡하고 시간이 많이 소요된다. 하지만 Naive Bayesian 분류기법은 모든 특성(feature)들이 독립적이다. 이것은 공분산이 없다는 것이므로 간단한 형태로 계산이 가능함을 말해준다.
문제를 정의하면 다음과 같다.

이것을 베이지안 공식에 적용하면 다음과 같다.

이것을 토대로 Naive Rule을 나타내면 다음과 같다.

또한

이것을 통해 다차원 문제를 1차원으로 축소시킬 수 있는 것을 확인할 수 있다.
Bayesian Belief Network
변수들의 관계를 acyclic network형태로 나타내는 것을 말한다.

이러한 네트워크가 형성되었다고 할때, 각 노드 (a, b, c)는 특성 또는 클래스를 나타낸다. 상호간의 연결은 조건부확률 (관계)를 나타낸다.
동시확률분포(joint probability) P(a,b,c)를 나타내면 다음과 같다.
조금 더 복잡한 예시로 설명해 보자.

노드간의 네트워크가 위 그림처럼 형성되었다고 할 때, 동시확률 분포는 다음과 같다.
좀 더 현실 반영이 된 예시를 들어보자.

이때 동시확률분포는 다음과 같다.
P(r,w,c,h,b) = p(r)p(w|r)p(c|r)p(h|w,r)p(b|w,c)