✍ Bayesian Decision
대학교에서 들은 ML course의 정리
Bayesian decison의 소개
베이지안 결정은 머신러닝에서 가장 기본이 된다. 우선 예시를 통해 베이지안 결정이 무엇인지 알아자.
Salmon - Sea Bass 문제
연어와 농어를 구분하기 위해 사람의 눈으로 구분가능하지만, 자동화 시스템에 의해 구분도 가능하다. 자동화 시스템에서는 생선 데이터에 대해 전처리를 진행한 후, 특성과 변수들을 추출한다. 이것들을 바탕으로 연어인지 농어인지 분류를 진행한다.
생선 데이터는 카메라에 의해 관찰된 데이터를 나타낸다. 관찰된 시각 데이터로 부터 길이, 밝기, 넓이 등 여러가지 시각적 특성 (feature)들을 추출할 수 있다.
해당 데이터 중 굵기 (width)와 밝기(lightness) 특성을 이용하여 시각화 된 데이터를 나타내면 다음과 같다.
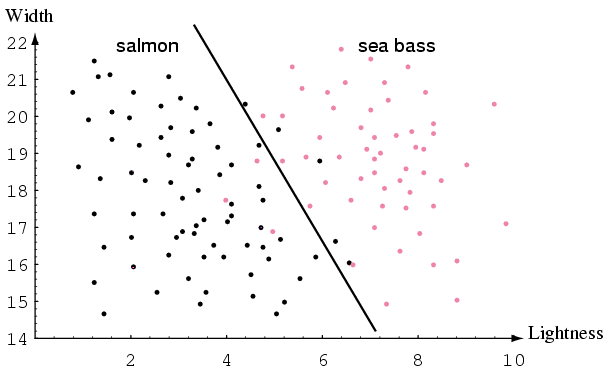
여기서 중간에 나타난 선은 decision boundary 또는 class boundary 또는 decision hyper plane이라고 부른다. 이 선에 의해 앞으로의 관측 데이터가 연어인지 농어인지 판단의 기준이 될 수 있다.
앞서 나타낸 연어와 농어 문제에서 생선 하나를 벡터로 나타낸 표현은 다음과 같다.
생선 → x^T = [x1, x2] x1: 밝기(lightness), x2: 굵기 (width)
이것을 토대로 여러마리 생선에 대한 데이터를 행렬로 나타내면 다음과 같다.
생선 → D = [x1^T, x2^T, ... xn^T]
Bayesian Classifier
우리는 데이터를 여러개의 클래스로 분류하려고 한다. 이때, 데이터들은 이산적(descrete)해야하고 특성이 있어야 한다. 앞서 예시를 들었던 salmon-sea bass 문제는 단순한 binary classification(이진 분류)라고 한다. 여기서 더 많은 클래스가 존재하면 multi-class classification(다항 분류)라고 한다.
베이지안 분류를 하기 전에 우리가 알고 싶어하는 정보가 있다
P(w_j | x) = x가 w_j에 속할 확률
(x: 데이터, w_j: j번째 클래스)
이것을 이용하여 binary classification의 경우
P(w_1 | x) + P(w_2 | x) = 1
이때 P(w1 | x) > P(w_2 | x) 인 경우, 데이터 x는 클래스 1에 해당한다.
Multi-class classification의 경우
P(w_1 | x), P(w_2 | x), ..., P(w_c | x)
베이지안 공식
베이지안 공식을 나타내면 다음과 같다.
P(A | B) = (P(A | B) P(A)) / p(B)
이 공식에 대한 설명은 확률과 통계에서 익히 배웠으므로 설명하지 않겠다.
이 모든것을 종합하여 베이지안 분류를 공식으로 나타내면 다음과 같다.
P(w_j | x) = (p(x | w_j) • P(w_j)) / P(x)
P(w_j | x): Posterior(사후 확률) P(x | w_j): Likelihood (비슷한 정도)
p(w_j): Prior (사전 확률) P(x): Evidence
Prior
Prior은 자연의 상태를 나타낸다. 자연의 상태임으로 랜덤 변수이다. Prior은 현재 측정하고 있는 데이터와 상관 없는 확률이다.
다시 Salman - Sea bass 문제로 돌아가본다. 노르웨이 해협에서 연어와 농어 단 두 종류의 생선만 존재한다고 가정한다. 이때 연어가 잡힐 확률은 2/3, 농어가 잡힐 확률은 1/3이라고 지정한다.
P(Salmon) = 2/3
p(Sea Bass) = 1/3
노르웨이 해협에서 연어인지 농어인지 판별하기 어려운 애매한 물고기가 잡혔다고 가정한다. 이때 사전확률(prior)을 개입하여 해당 물고기가 연어임으로 분류한다.
다른 예시로 한 도시에 외제차 수입차의 분포의 사전 지식을 다음과 같다고 하자.
P(국산차) = 3/4
P(수입차) = 1/4
현재 관측된 차량이 수입차 (ex OOOO마크인 아우디 차량)인 경우 수입차 임이 명확히 판별이 가능하다. 하지만 수입차인지 국산차인지 알 수 없는 경우, 사전지식을 도입하여 해당 차량이 국산차일 확률이 높으므로 국산차로 분류한다.
Likelihood
Likelihood는 현재 관측된 데이터의 빈도를 나타낸다. 이것을 class-conditional probability(클래스 조건부 확률)이라고 부른다.
앞서 예시를 들었던 Salmon - Sea Bass의 문제의 클래스 조건부 확률을 나타내면 다음과 같다.

여기서 w_2 와 w_1 의 만나는 지점(x = 약 12.5)에서 w_2가 높은 쪽은 연어로 분류되고, w__1이 높은 쪽은 농어로 분류된다.
Evidence
Evidence는 Posterior을 확률 분포로 나타내기위한 요소로 사용된다. 따라서 이것을 scale factor라고 한다. 이것은 베이지안 결정식에서 j와 무관하다. 즉 데이터의 class 분류에 영향을 주지 않는다.
Posterior
클래스 분류의 확률을 나타내는 것이다. 앞서 설명한 3가지 속성을 종합한 결과이다. Posterior은 likelihood prior에 비례한다. 여기서 evidence는 마찬가지로 의미가 없다. 따라서 결정은 likelihood prior에 의해 결정이 된다.
P(w_1 | x) -> P(x | w_1) • P(w_1)
P(w_2 | x) -> P(x | w_2) • P(w_2) 일때
P(w_1 | x) > P(w_2 | x) → class 1
P(w_1 | x) < P(w_2 | x) → class 2
Likelihood와 Posterior의 관계
Posterior은 Likelihood에 prior을 곱한 값이다. 앞서 예시를 들었던 Salmon - Sea Bass 문제의 likelihood에 prior을 곱하면 전혀 다른 그래프가 그려질 것이다.
Prior을 Salmon(P(w_1))의 확률 2/3, Sea-Bass(P(w_2))의 확률 1/3을 곱한 결과는 다음과 같다.

Posterior에 의한 결정
우리가 prior을 알고 데이터 X를 관측했을 때 분류는 다음과 같다.
P(w_1 | x) > P(w_2 | x) 일때 Decision = w_1
P(w_1 | x) < P(w_2 | x) 일때 Decision = w_2
이때 에러의 확률은 다음과 같다.
P(w_1 | x) > P(w_2 | x) 일때 Error = P(w_2 | x)
P(w_1 | x) < P(w_2 | x) 일때 Error = P(w_1 | x)
이것을 통해 비교되는 두 Posterior의 Max 값은 결정(Decision)이 되고 Min은 Error이 된다.
에러의 확률 식을 나타내면 다음과 같다.
P(error | x ) = min [P(w_1 | x), p(w_2 | x)]

