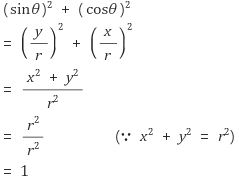이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy
지난 시간에 외적에 대해 배워본 것을 바탕으로,
외적과 sin간의 관계에 대해 증명해보고자 한다.
 벡터 a, b의 내적은 각각 벡터 a와 b의 크기를 곱한 것에 cos θ를 해준 것과 같이 표현할 수 있다고 이전에 배웠다.
벡터 a, b의 내적은 각각 벡터 a와 b의 크기를 곱한 것에 cos θ를 해준 것과 같이 표현할 수 있다고 이전에 배웠다.
그렇다면 벡터 a, b의 외적은 무엇일까?
벡터 a, b의 외적의 절대값은 벡터 a, b의 크기를 곱한 것에 sin θ이다.
⭐ ∣∣a×b∣∣ = ∣∣(a)∣∣ ∣∣(b)∣∣ sin θ ⭐
이를 증명하기 위해 외적의 절댓값을 제곱해보고자 한다.
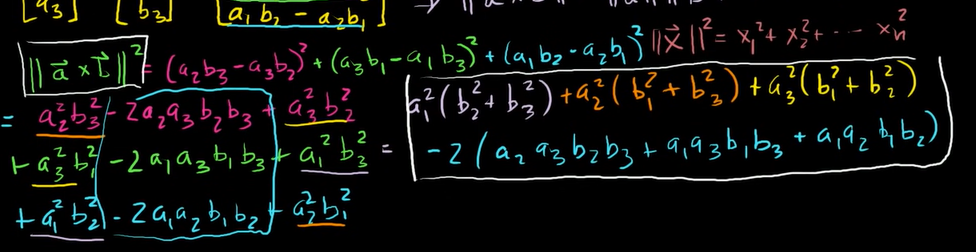 ∣∣(a×b)∣∣2 를 제곱해보자.
∣∣(a×b)∣∣2 를 제곱해보자.
∣∣(x)∣∣2 = (x1)2+(x2)2+…(xn)2
이처럼 외적의 절댓값의 제곱은
= 외적하는 벡터의 각 성분을 제곱한 것의 합으로 표현할 수 있다.
∣∣(a×b)∣∣2 식을 풀어서 정리하면,
(a1)2(b22+b32)+(a2)2(b12+b32)+(a3)2(b12+b22)− 2(a1a3b2b3+a1a3b1b3+a1a2b1b2) 가 된다.
이번에는 벡터의 내적을 제곱해보고자 한다.
(벡터 외적과 sin과의 관계를 증명하기 위한 과정이니 일단은 해보도록 하자.)

∣∣(a)∣∣ ∣∣(b)∣∣ cos θ = (a⋅b)2 = (a1b1+a2b2+a3b3)2 에서
(a1b1+a2b2+a3b3)2 는 (a1b1+a2b2+a3b3)×(a1b1+a2b2+a3b3)과 같으므로, 아래와 같이 식을 정리할 수 있다.
∣∣(a)∣∣ ∣∣(b)∣∣ cos θ
= a12b12+a22b22+a32b32+ 2(a1a2b1b2+a1a3b1b3+a2a3b2b3)
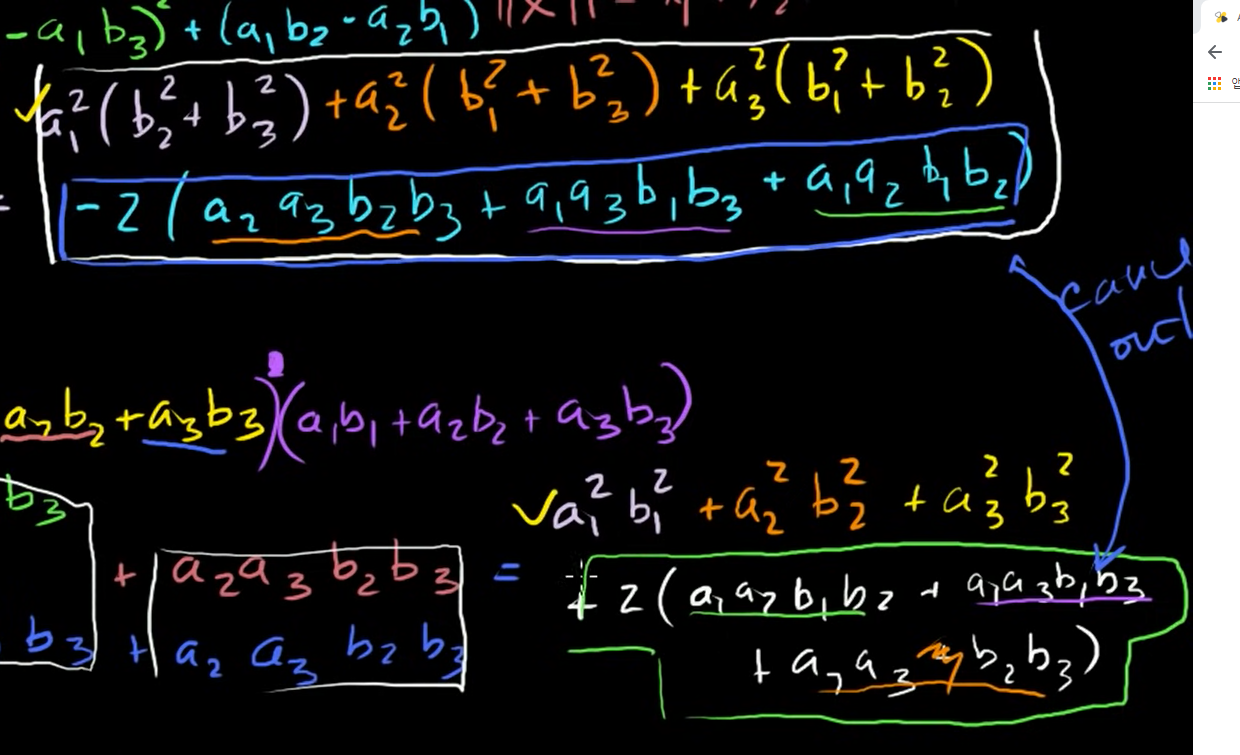 ∣∣(a×b)∣∣2, ∣∣(a)∣∣ ∣∣(b)∣∣ cos θ 이 2개의 식을 풀어서 정리했을 때,
∣∣(a×b)∣∣2, ∣∣(a)∣∣ ∣∣(b)∣∣ cos θ 이 2개의 식을 풀어서 정리했을 때,
2(a1a2b1b2+a1a3b1b3+a2a3b2b3) 이 부분이 같으므로 없에주기 위해 식을 더해보자.
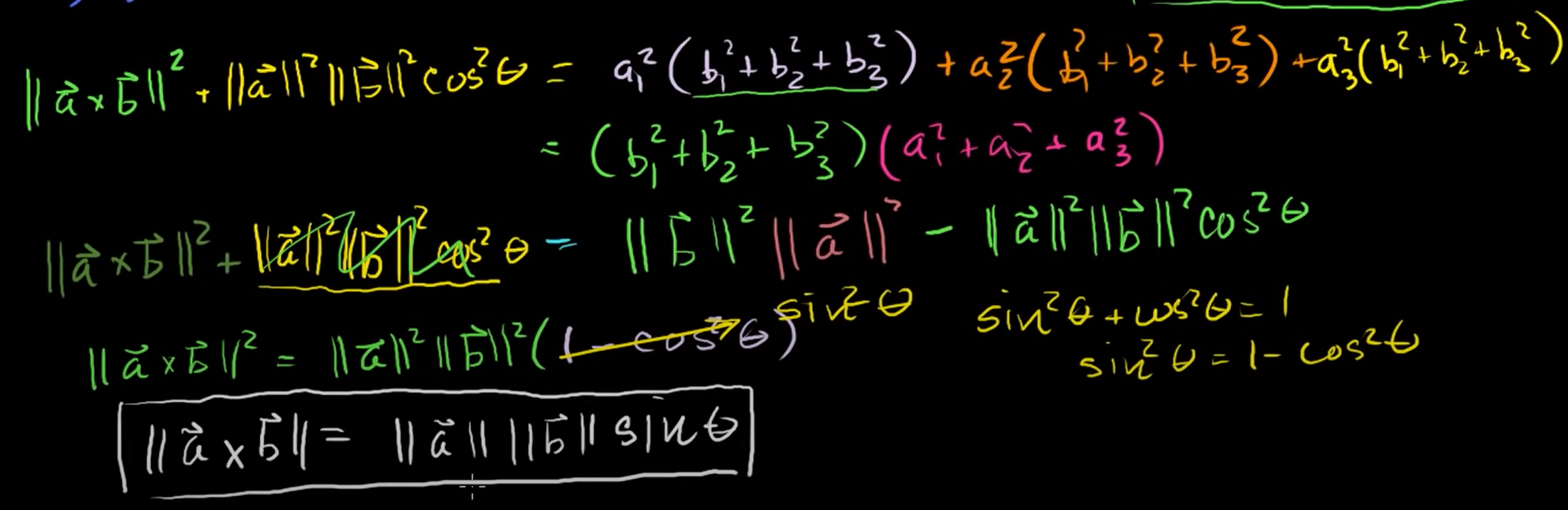 ∣∣(a×b)∣∣2+∣∣(a)∣∣2 ∣∣(b)∣∣2 cos2 θ
∣∣(a×b)∣∣2+∣∣(a)∣∣2 ∣∣(b)∣∣2 cos2 θ
= (b12+b22+b32)(a12+a22+a32)
= ∣∣b∣∣2 ∣∣a2∣∣ 로 표현할 수 있다.
좌변에 있던 ∣∣(a)∣∣2 ∣∣(b)∣∣2 cos2 θ 를 우변으로 옮겨주자.
∣∣(a×b)∣∣2 = ∣∣(a)∣∣2 ∣∣(b)∣∣2 (1−cos2 θ) 이므로,
최종적으로 ∣∣(a)∣∣ ∣∣(b)∣∣ sin2 θ가 도출된다.
⭐ 여기서 잠깐 !
1. sin과 cos간의 관계를 상기시켜보자.
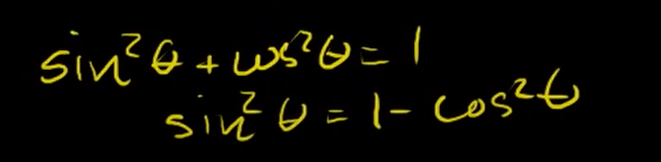
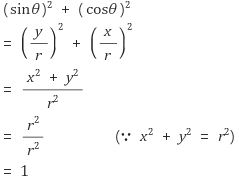
위 식이 성립할 수 있는 이유이다.
2. 벡터의 크기를 아래와 같은 식으로 표현할 수 있다는 것을 기억하는가?
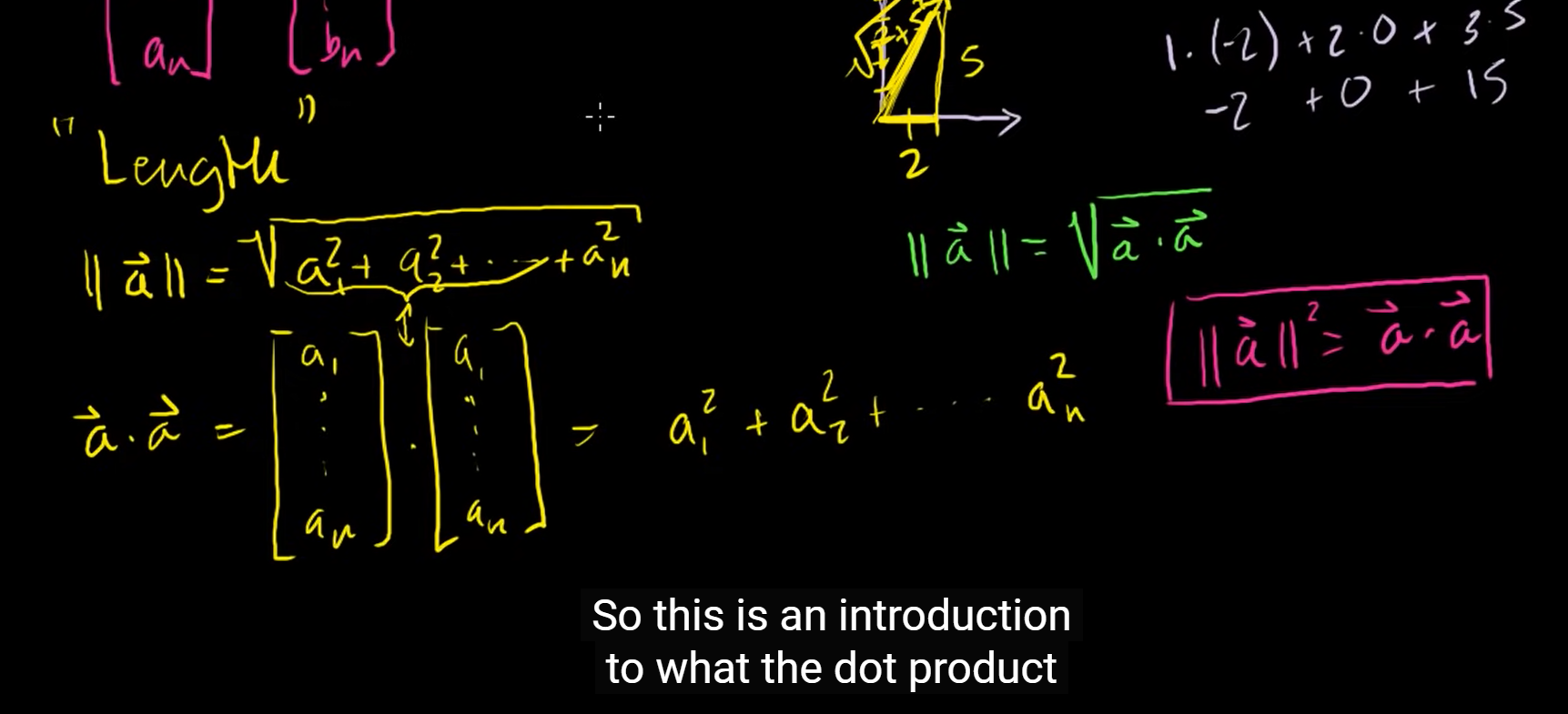 ∣∣(a)∣∣ = a12+a22+⋯+an2
∣∣(a)∣∣ = a12+a22+⋯+an2
각 변을 제곱해주면,
∣∣(a)∣∣2 = (a⋅a) = a12+a22+⋯+an2
이렇게 방금 위에서 얻은 낯이 익은 식을 도출해낼 수 있다.
오늘은 여기까지 ,,,
 벡터 a, b의 내적은 각각 벡터 a와 b의 크기를 곱한 것에 cos 를 해준 것과 같이 표현할 수 있다고 이전에 배웠다.
벡터 a, b의 내적은 각각 벡터 a와 b의 크기를 곱한 것에 cos 를 해준 것과 같이 표현할 수 있다고 이전에 배웠다. 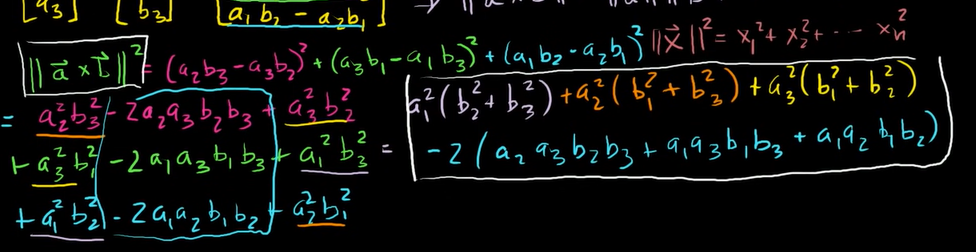 를 제곱해보자.
를 제곱해보자. 
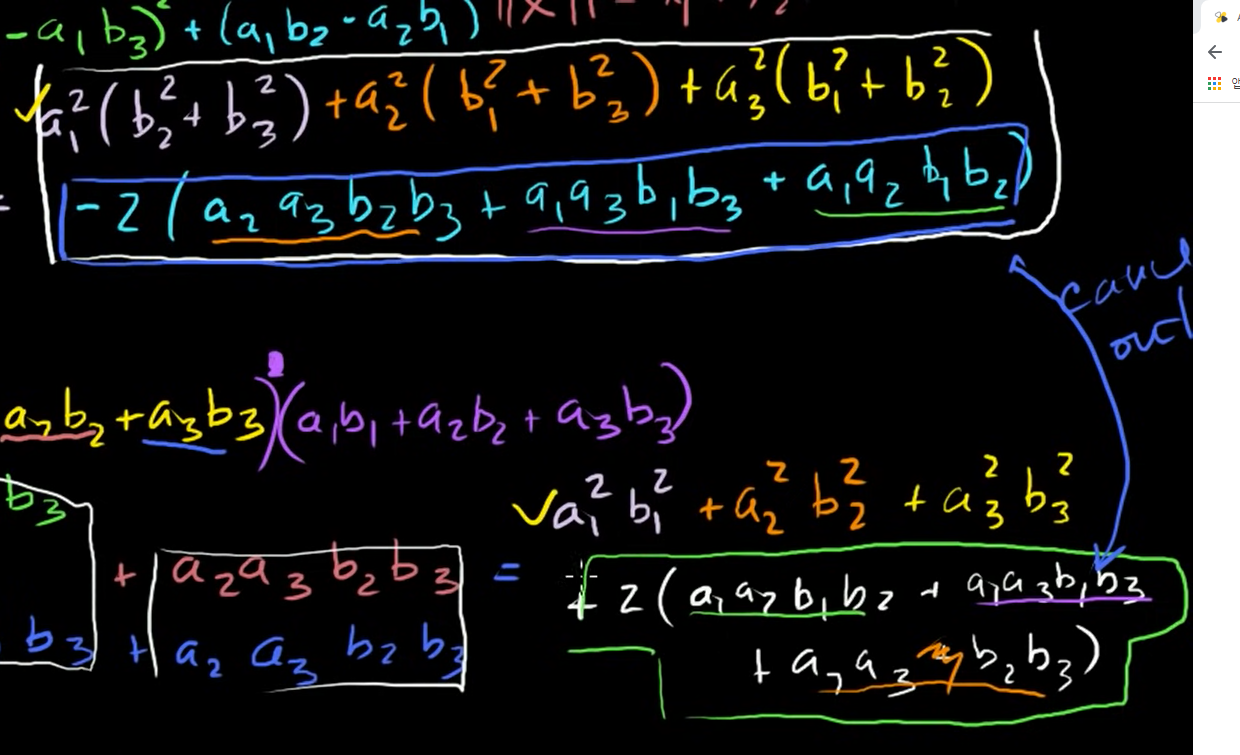 , 이 2개의 식을 풀어서 정리했을 때,
, 이 2개의 식을 풀어서 정리했을 때, 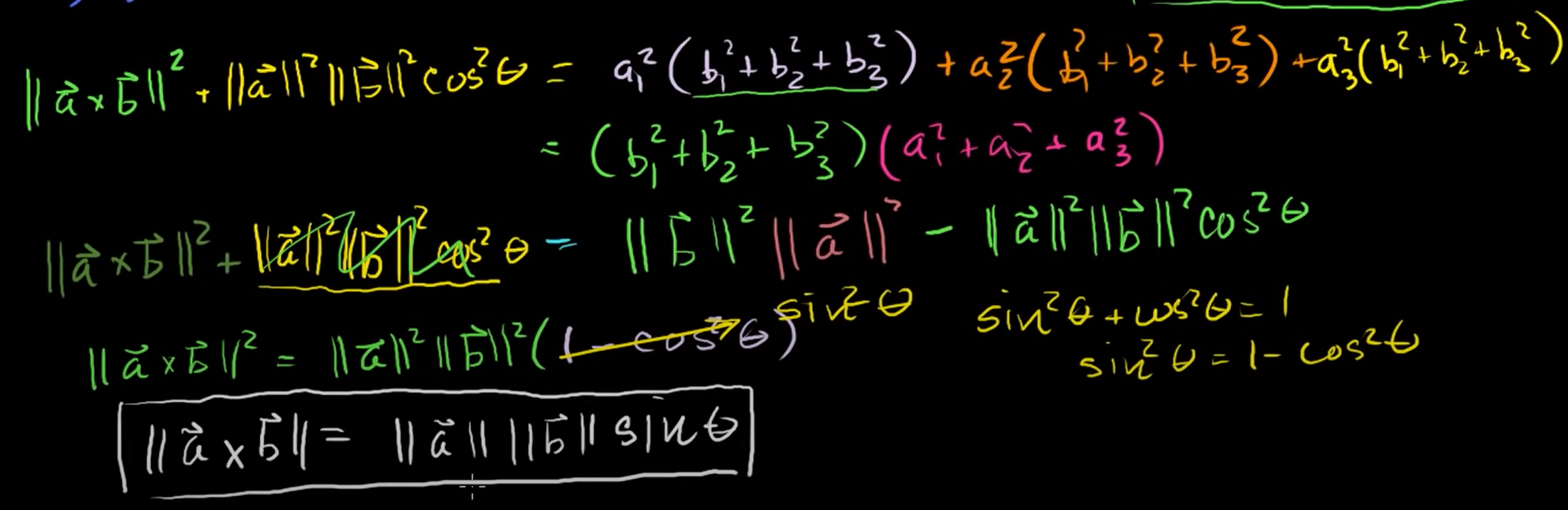
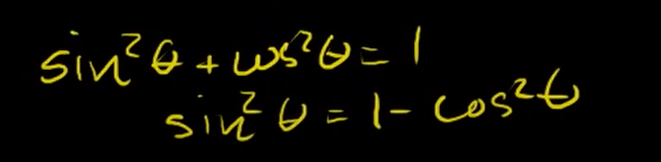
=