Linear Algebra
1.[Linear algebra] Day 1. Vectors

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다. 링크: Khan academy5mph는 속력(speed)이며 scalar값이다.방향까지 더해진 경우 속도(velocity)이며 vector값이다.$$R^2$$은 2차원 유클
2.[Linear algebra] Day 2. Vectors

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academyVector v를 $$\\overrightarrow{v}$$ = (2, 3)라는 column vector로 표현할 수 있지만 $$\\overrig
3.[Linear algebra] Day 3. Linear combinations and spans

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy선형 결합, 말 그대로 선형 직선들의 덧셈이다. $C_1$$V_1$ + $C_2$$V_2$ + $$\\dots$$ + $C_n$$V_n$ 스칼라값
4.[Linear algebra] Day 4. Introduction to linear independence
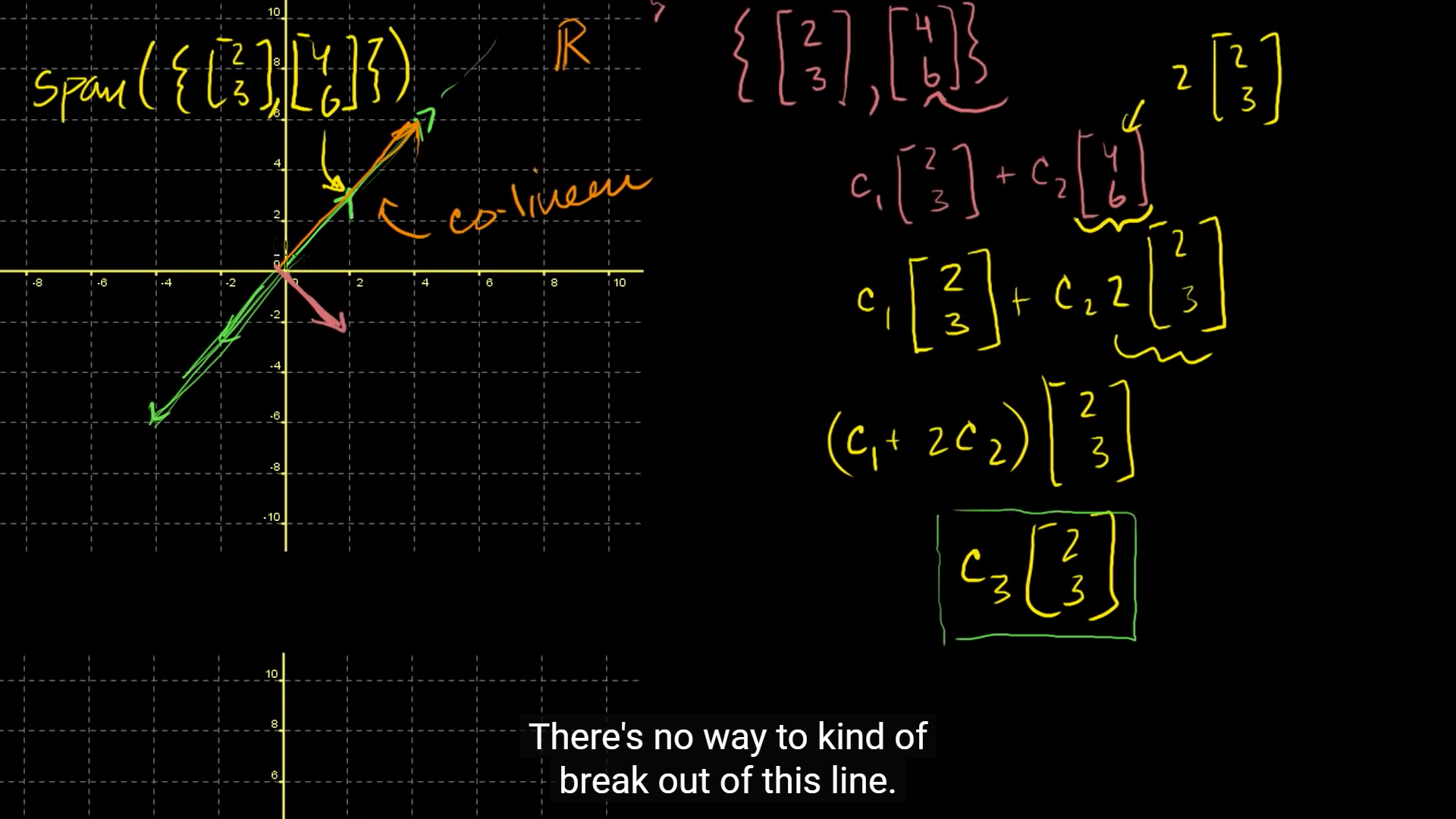
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy이번 강의에서는 '선형 독립성'에 대한 내용을 다룬다. 만일 두 개의 vector 중 하나가 첫번째 vector의 스칼라(arbitrary co
5.[Linear algebra] Day 5. Linear dependence and independence
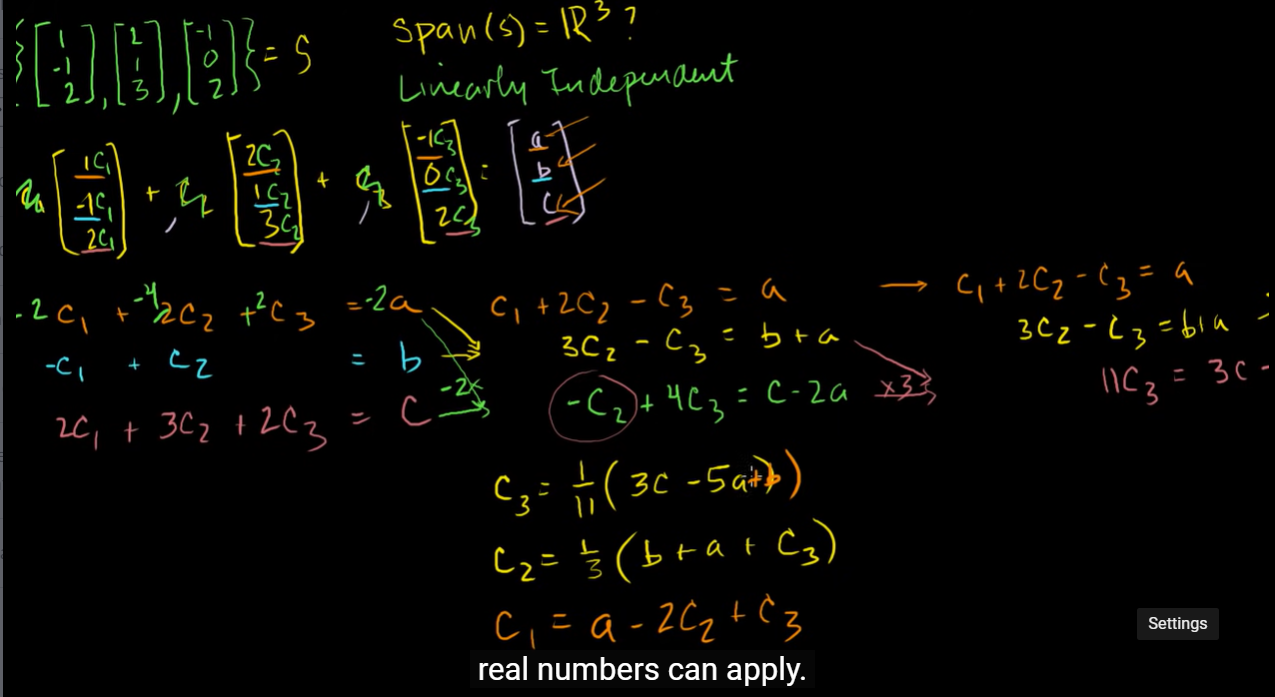
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academySpan and linear independence example
6.[Linear algebra] Day 11. Defining the angle between vectors
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy
7.[Linear Algebra] Day 14. Proof: Relationship between cross product and sin of angle

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy지난 시간에 외적에 대해 배워본 것을 바탕으로, 외적과 sin간의 관계에 대해 증명해보고자 한다. 벡터 a, b의 내적은 각각 벡터 a와 b의 크
8.[Linear Algebra] Day 13. Cross product introduction

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy벡터의 외적을 구하는 방법이다. 내적은 $R^3$인 3차원에서만 성립한다.외적 결과로 나온 벡터는 외적한 벡터 a, b와 직교(orthogona
9.[Linear Algebra] Day 18. Solving a system of 3 equations and 4 variables using matrix row-echelon form
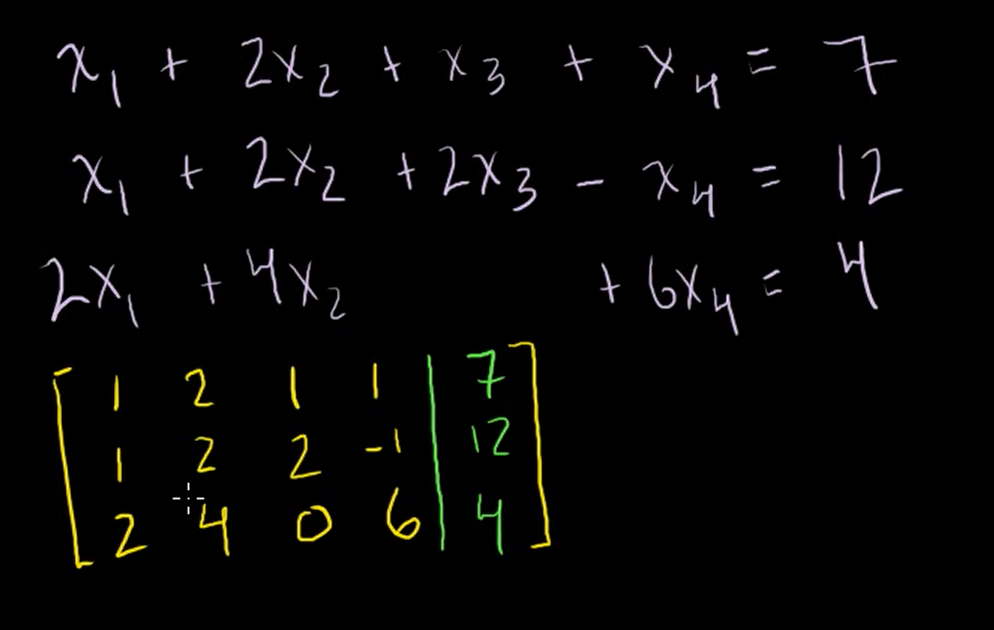
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy즉, 연랍방적식들의 계수행렬을 만드는 것인데, 선을 기준으로 오른쪽은 첨가행렬로 방정식들을 쓰는 다른 방법일 뿐이다. 이렇게 함으로써 스칼라 방정
10.[Linear Algebra] Day 21. Matrix vector products
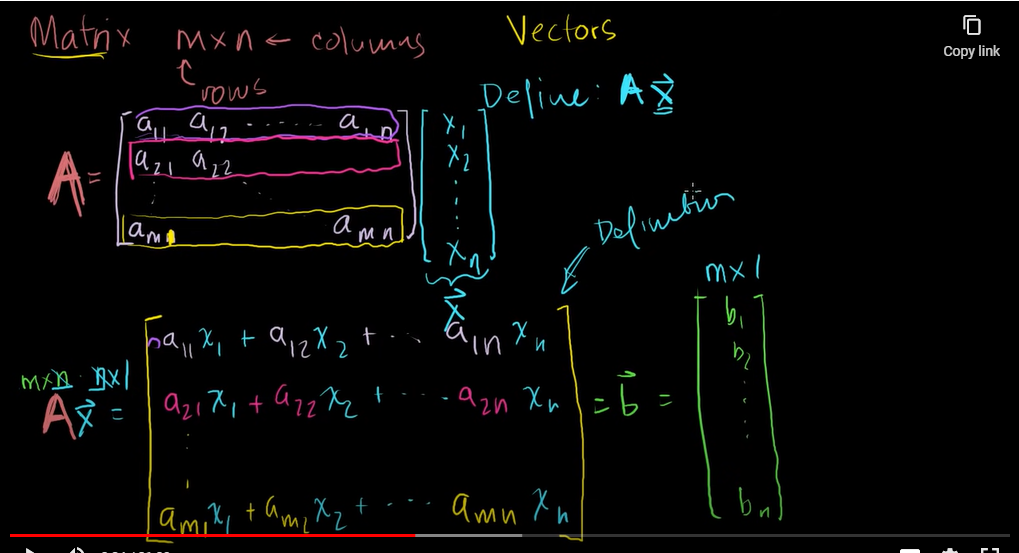
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy행렬과 벡터의 곱에 대해 알아보자. $$A = m \\times n$$와 $$\\overrightarrow{x} = \\begin{bmatrix}
11.[Linear Algebra] Day 37. Transpose of a matrix

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy 선형대수 ,, 재밌다 ,,
12.[Linear algebra] Day 42. rank(a) = rank(transpose of A)
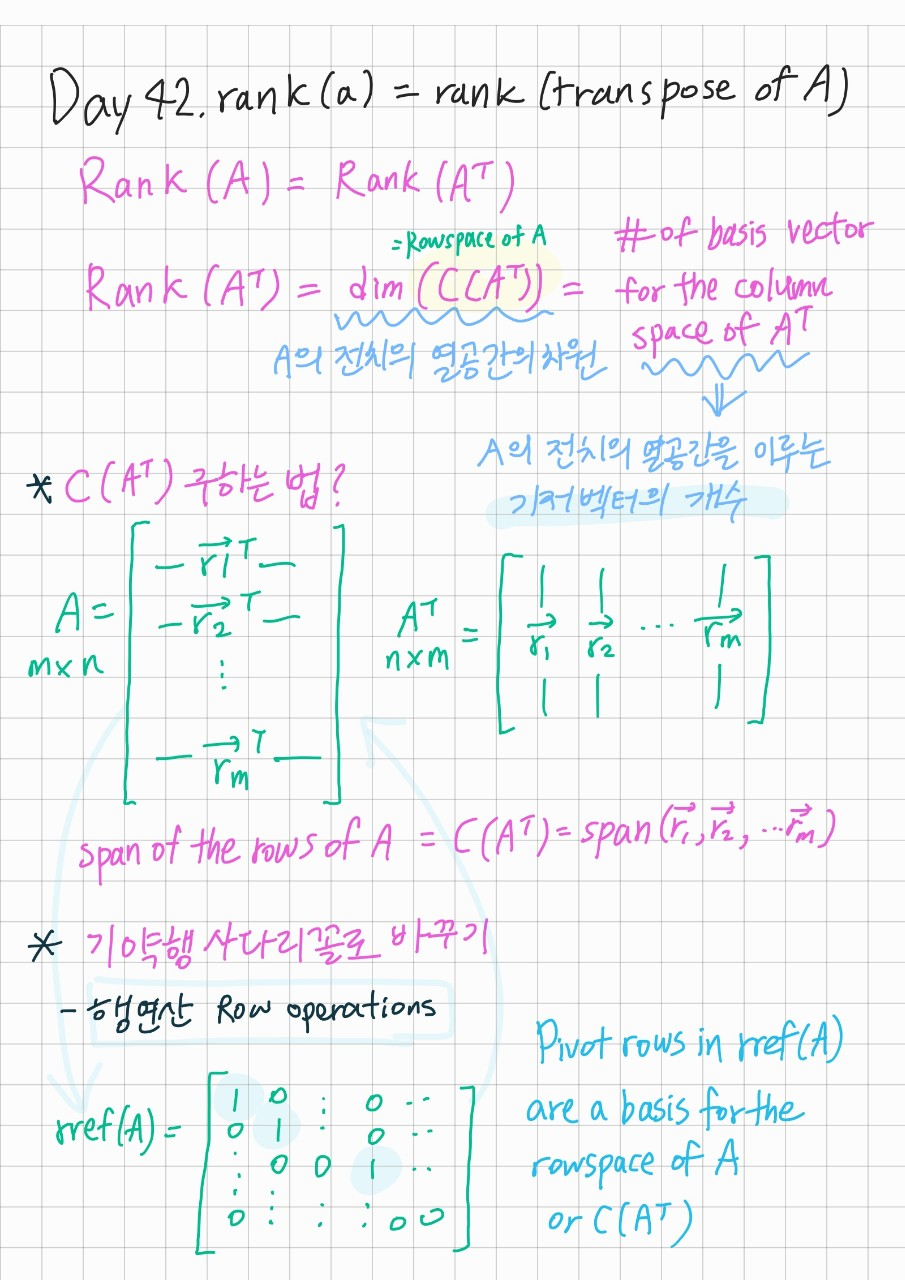
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.링크: Khan academy(https://www.khanacademy.org/math/linear-algebra열벡터의 개수가 계수가 된다는 말 ! 이전 강의에서