[Do it! 딥러닝] 5장 리뷰 - 훈련 노하우

1. 검증 세트 나누기

테스트 세트로 모델을 튜닝하면 테스트 세트의 정보가 모델에 새어 나가므로 모델의 일반화 성능이 왜곡됨. (낙관적 추정)

이를 방지하고자 모델을 튜닝하는 용도로 검증세트를 준비함. 검증세트는 훈련세트에서 분할하여 만듦. (최근에는 데이터 크기가 매우 커졌기 때문에 6:2:2 분할에서 98:1:1 분할로 바뀜)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDClassifier

cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x, y, stratify=y, 
                                                            test_size=0.2, random_state=42)
                                                            
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, 
                                                  test_size=0.2, random_state=42)

모델 평가

sgd = SGDClassifier(loss='log', random_state=42)
sgd.fit(x_train, y_train)
sgd.score(x_val, y_val)

0.6923076923076923
데이터 양이 너무 적기 때문에 성능이 낮았음. 이 경우 교차 검증을 사용함

2. 스케일 조정

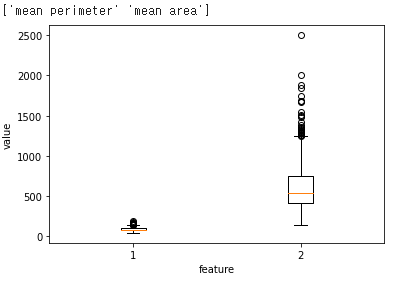
두 특성간의 스케일 비교

print(cancer.feature_names[[2,3]])
plt.boxplot(x_train[:, 2:4])
plt.xlabel('feature')
plt.ylabel('value')
plt.show()

mean perimeter -> 100~200
mean area -> 200~2000 로 두 특성간의 스케일이 매우 다름

단일층 신경망 뉴런

class SingleLayer:
    
    def __init__(self, learning_rate=0.1, l1=0, l2=0):
        self.w = None
        self.b = None
        self.losses = []
        self.val_losses = []
        self.w_history = []
        self.lr = learning_rate
        self.l1 = l1
        self.l2 = l2

    def forpass(self, x):
        z = np.sum(x * self.w) + self.b    # 직선 방정식을 계산합니다
        return z

    def backprop(self, x, err):
        w_grad = x * err          # 가중치에 대한 그래디언트를 계산합니다
        b_grad = 1 * err    # 절편에 대한 그래디언트를 계산합니다
        return w_grad, b_grad

    def activation(self, z):
        z = np.clip(z, -100, None) # 안전한 np.exp() 계산을 위해
        a = 1 / (1 + np.exp(-z))  # 시그모이드 계산
        return a
        
    def fit(self, x, y, epochs=100, x_val=None, y_val=None):
        self.w = np.ones(x.shape[1])               # 가중치를 초기화합니다.
        self.b = 0                                 # 절편을 초기화합니다.
        self.w_history.append(self.w.copy())       # 가중치를 기록합니다.
        np.random.seed(42)                         # 랜덤 시드를 지정합니다.
        for i in range(epochs):                    # epochs만큼 반복합니다.
            loss = 0
            # 인덱스를 섞습니다
            indexes = np.random.permutation(np.arange(len(x)))
            for i in indexes:                      # 모든 샘플에 대해 반복합니다
                z = self.forpass(x[i])             # 정방향 계산
                a = self.activation(z)             # 활성화 함수 적용
                err = -(y[i] - a)                  # 오차 계산
                w_grad, b_grad = self.backprop(x[i], err) # 역방향 계산
                # 그래디언트에서 페널티 항의 미분 값을 더합니다
                w_grad += self.l1 * np.sign(self.w) + self.l2 * self.w
                self.w -= self.lr * w_grad         # 가중치 업데이트
                self.b -= self.lr * b_grad         # 절편 업데이트
                # 가중치를 기록합니다.
                self.w_history.append(self.w.copy())
                # 안전한 로그 계산을 위해 클리핑한 후 손실을 누적합니다
                a = np.clip(a, 1e-10, 1-1e-10)
                loss += -(y[i]*np.log(a)+(1-y[i])*np.log(1-a))
            # 에포크마다 평균 손실을 저장합니다
            self.losses.append(loss/len(y) + self.reg_loss())
            # 검증 세트에 대한 손실을 계산합니다
            self.update_val_loss(x_val, y_val)
    
    def predict(self, x):
        z = [self.forpass(x_i) for x_i in x]     # 정방향 계산
        return np.array(z) >= 0                   # 스텝 함수 적용
    
    def score(self, x, y):
        return np.mean(self.predict(x) == y)
    
    def reg_loss(self):
        return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w**2)
    
    def update_val_loss(self, x_val, y_val):
        if x_val is None:
            return
        val_loss = 0
        for i in range(len(x_val)):
            z = self.forpass(x_val[i])     # 정방향 계산
            a = self.activation(z)         # 활성화 함수 적용
            a = np.clip(a, 1e-10, 1-1e-10)
            val_loss += -(y_val[i]*np.log(a)+(1-y_val[i])*np.log(1-a))
        self.val_losses.append(val_loss/len(y_val) + self.reg_loss())

스케일 조정하지 않은 모델의 성능

layer1 = SingleLayer()
layer1.fit(x_train, y_train)
layer1.score(x_val, y_val)

0.9120879120879121

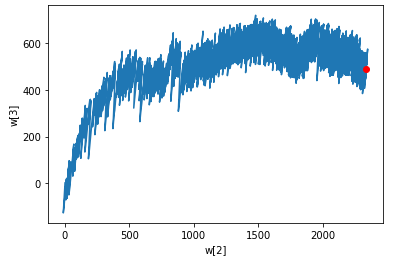
스케일 조정하지 않은 모델의 가중치

w2 = []
w3 = []
for w in layer1.w_history:
    w2.append(w[2])
    w3.append(w[3])
plt.plot(w2, w3)
plt.plot(w2[-1], w3[-1], 'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()

가중치가 크게 요동치고 있음. 모델이 불안정하게 수렴한다. 이런 경우 스케일 조정

스케일을 조정하는 방법은 소프트맥스, 표준화, 정규화 등 여러가지가 있다. 이번 리뷰에서는 표준화를 사용하였다.

train_mean = np.mean(x_train, axis=0)
train_std = np.std(x_train, axis=0)
x_train_scaled = (x_train - train_mean) / train_std

layer2 = SingleLayer()
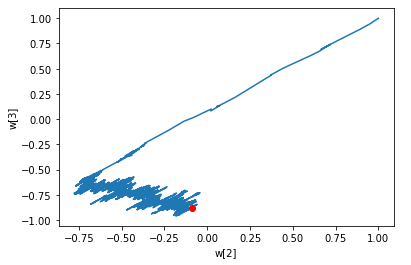
layer2.fit(x_train_scaled, y_train)

가중치 그래프

w2 = []
w3 = []
for w in layer2.w_history:
    w2.append(w[2])
    w3.append(w[3])
plt.plot(w2, w3)
plt.plot(w2[-1], w3[-1], 'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()

이전 그래프와는 확실히 다른 결과. 두 특성의 스케일을 비슷하게 맞추었으므로 최적값에 빠르게 근접함.

모델 성능 평가

val_mean = np.mean(x_val, axis=0)
val_std = np.std(x_val, axis=0)
x_val_scaled = (x_val - val_mean) / val_std
layer2.score(x_val_scaled, y_val)

0.967032967032967

3. 규제

규제 - 과대적합을 해결하는 대표적인 방법 중 하나

L1 규제

l1_list = [0.0001, 0.001, 0.01]

for l1 in l1_list:
    lyr = SingleLayer(l1=l1)
    lyr.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val)
    
    plt.plot(lyr.losses)
    plt.plot(lyr.val_losses)
    plt.title('Learning Curve (l1={})'.format(l1))
    plt.ylabel('loss')
    plt.xlabel('epoch')
    plt.legend(['train_loss', 'val_loss'])
    plt.ylim(0, 0.3)
    plt.show()
    
    plt.plot(lyr.w, 'bo')
    plt.title('Weight (l1={})'.format(l1))
    plt.ylabel('value')
    plt.xlabel('weight')
    plt.ylim(-4, 4)
    plt.show()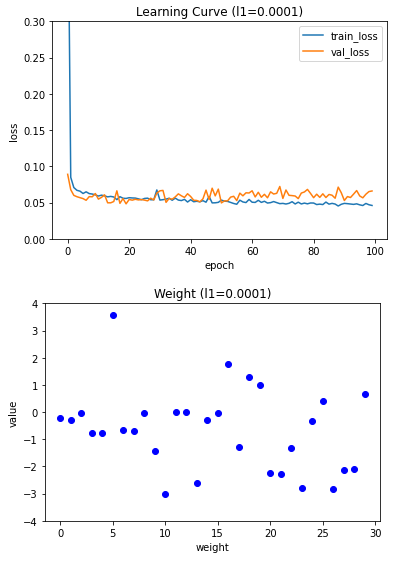

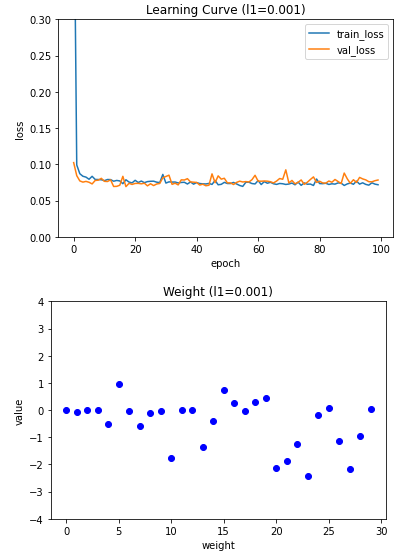
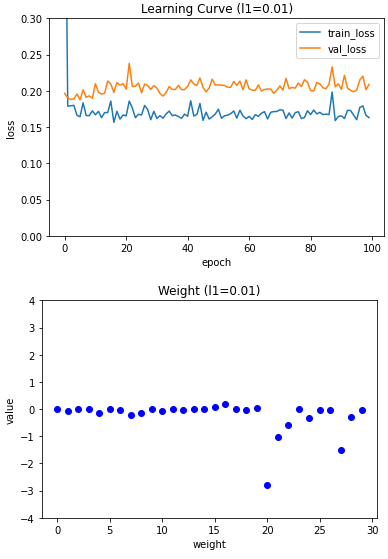
규제 강도가 커질수록 가중치의 값이 0에 가까워지는 것을 볼 수 있다. 적절한 L1 하이퍼파라미터 값은 0.001 이므로 L1이 0.001때의 성능 측정

layer5 = SingleLayer(l1=0.001)
layer5.fit(x_train_scaled, y_train, epochs=20)
layer5.score(x_val_scaled, y_val)

0.989010989010989

L2 규제

l2_list = [0.0001, 0.001, 0.01]

for l2 in l2_list:
    lyr = SingleLayer(l2=l2)
    lyr.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val)
    
    plt.plot(lyr.losses)
    plt.plot(lyr.val_losses)
    plt.title('Learning Curve (l2={})'.format(l2))
    plt.ylabel('loss')
    plt.xlabel('epoch')
    plt.legend(['train_loss', 'val_loss'])
    plt.ylim(0, 0.3)
    plt.show()
    
    plt.plot(lyr.w, 'bo')
    plt.title('Weight (l2={})'.format(l2))
    plt.ylabel('value')
    plt.xlabel('weight')
    plt.ylim(-4, 4)
    plt.show()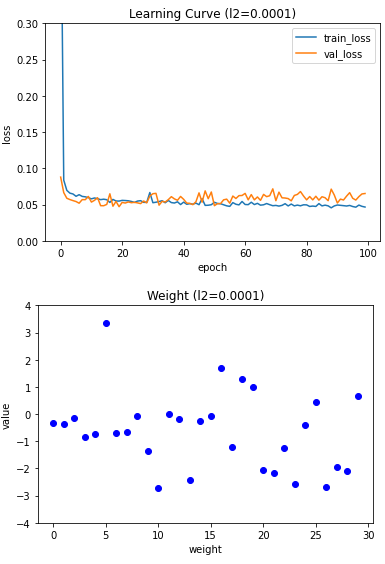

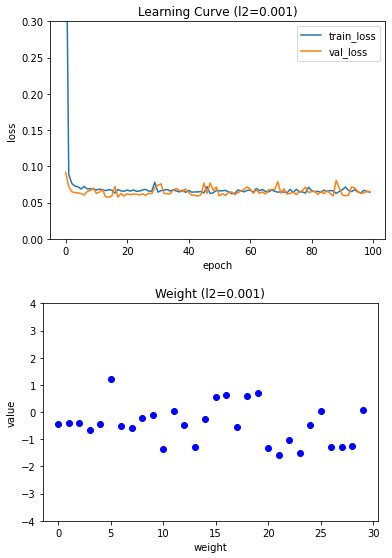
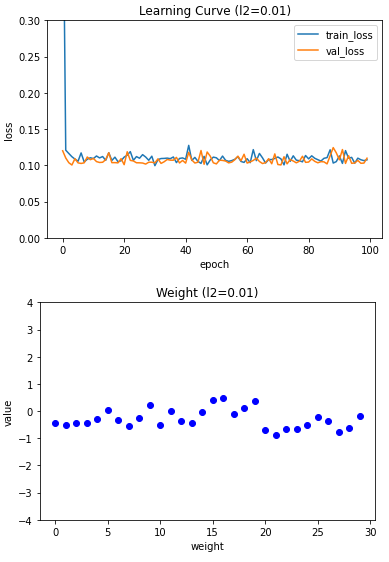
L2 규제는 강도가 강해져도 L1 규제만큼 과소적합이 심해지지는 않기 때문에 0.01로 성능 평가

layer6 = SingleLayer(l2=0.01)
layer6.fit(x_train_scaled, y_train, epochs=50)
layer6.score(x_val_scaled, y_val)

0.989010989010989

4. 교차 검증

전체 데이터 세트의 샘플 개수가 많지 않을 때 사용하는 방법

validation_scores = []

k = 10
bins = len(x_train_all) // k

for i in range(k):
    start = i*bins
    end = (i+1)*bins
    val_fold = x_train_all[start:end]
    val_target = y_train_all[start:end]
    
    train_index = list(range(0, start))+list(range(end, len(x_train_all)))
    train_fold = x_train_all[train_index]
    train_target = y_train_all[train_index]
    
    train_mean = np.mean(train_fold, axis=0)
    train_std = np.std(train_fold, axis=0)
    train_fold_scaled = (train_fold - train_mean) / train_std
    val_fold_scaled = (val_fold - train_mean) / train_std
    
    lyr = SingleLayer(l2=0.01)
    lyr.fit(train_fold_scaled, train_target, epochs=50)
    score = lyr.score(val_fold_scaled, val_target)
    validation_scores.append(score)

print(np.mean(validation_scores))

0.9777777777777779