2022 0307 TIL & 회고

더 공부해볼 내용

• 이진 트리와 BST 이외에 어떠한 트리가 있을까요?
• 균형 이진 탐색 트리란 무엇일까요?
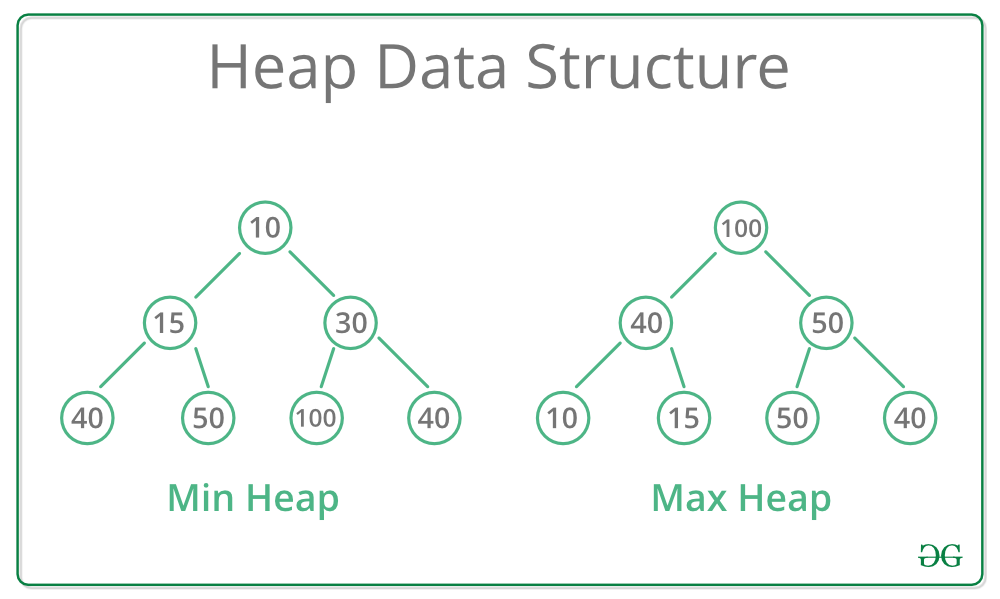
• (Advanced) 힙이란 무엇일까요? 힙은 트리가 완전한 이진 트리인 특수한 트리 기반 데이터 구조입니다. 일반적으로 힙에는 두 가지 유형이 있습니다.

  1. Max-Heap

     : Max-Heap에서 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 커야 합니다. 이진 트리의 모든 하위 트리에 대해 동일한 속성이 재귀적으로 true여야 합니다.

  2. Min-Heap

     : Min-Heap에서 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 최소여야 합니다. 이진 트리의 모든 하위 트리에 대해 동일한 속성이 재귀적으로 true여야 합니다.

     

• DFS와 BFS의 장단점은 또 무엇이 있을까요?

  Breadth First Search

  BFS stands for Breadth First Search is a vertex based technique for finding a shortest path in graph. It uses a Queue data structure which follows first in first out. In BFS, one vertex is selected at a time when it is visited and marked then its adjacent are visited and stored in the queue. It is slower than DFS. Ex- 

          A
         / \
        B   C
       /   / \
      D   E   F

  Output is: 

  A, B, C, D, E, F

  Depth First Search

  DFS stands for Depth First Search is a edge based technique. It uses the Stack data structure, performs two stages, first visited vertices are pushed into stack and second if there is no vertices then visited vertices are popped. Ex- 

          A
         / \
        B   C
       /   / \
      D   E   F

  Output is: 

  A, B, D, C, E, F

  BFS vs DFS

  
• 그래프가 굉장히 크다면 어떤 탐색 기법을 고려해야 할까요? DFS : Stack,재귀로 구현
  
• 반대로, 그래프의 규모가 작고, depth가 얕다면 어떤 탐색 기법을 고려해야 할까요? BFS : Queue로 구현

레퍼런스

• 반대로, 그래프의 규모가 작고, depth가 얕다면 어떤 탐색 기법을 고려해야 할까요? BFS : Queue로 구현

Big O

알고리즘 스피드는 “완료까지 걸리는 절차의 수"로 결정 된다.

Big O를 이해한다면?

• 시간 복잡도를 쉽게 설명 할 수 있다.
• 알고리즘 분석을 빠르게 하고 언제 무엇을 쓸지 결정.
• 자신의 코드를 평가 할 수 있다.

0(1)

let arr = [1,2,3,.....100];
	function printFirst(arr) {
	console.log(arr[0]);
}

printFirst 함수의 시간복잡도를 BigO로 표현하면?

인풋이 몇개가 되든 printFirst 함수는 첫번째 요소를 한번 출력하므로 시간 복잡도는 상수 시간(constant time)이다. ⇒ O(1)

let arr = [1,2,3,.....100];
	function printThreeTimes(arr) {
		console.log(arr[0]);
		console.log(arr[0]);
		console.log(arr[0]);
}

그렇다면 위 함수인 경우엔 O(3)일까?

BigO는 함수의 디테일에 관계없이 인풋 사이즈에 따라서 함수가 어떻게 작동하는지를 표현할 뿐이다.

3은 상수이고 빅오에서 상수는 무시한다.

인풋이 몇개든 관계없이 스텝이 정해진 알고리즘이므로 빅오는 ⇒ O(1)

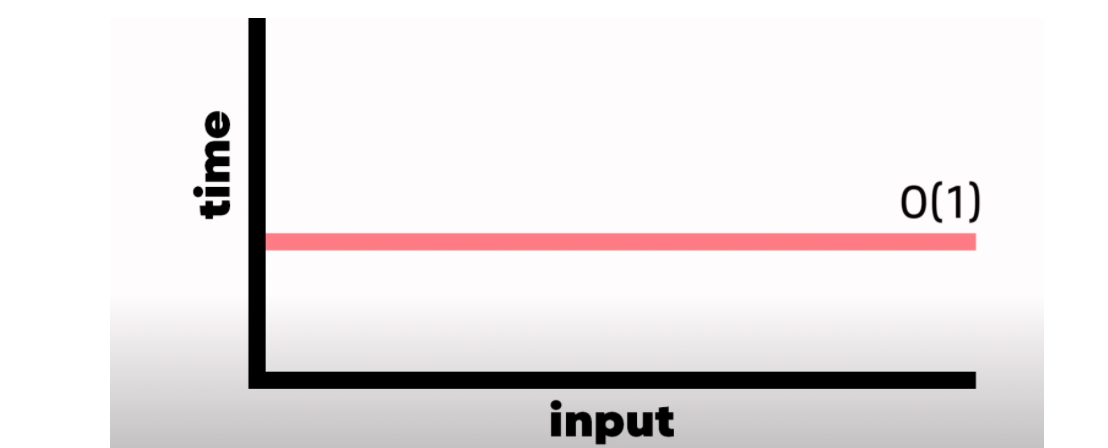
만약 선형 검색(Linear Search)에서 input size 가 = N 이라면 N 스텝이 요구 된다.

⇒ 한번에 표현 : 선형검색의 시간 복잡도 = 0(N)

0(N)

function print_all(arr) {
	for (let item of arr) {
		console.log(item) 
	};
	for (let item of arr) {
		console.log(item) 
	};
}
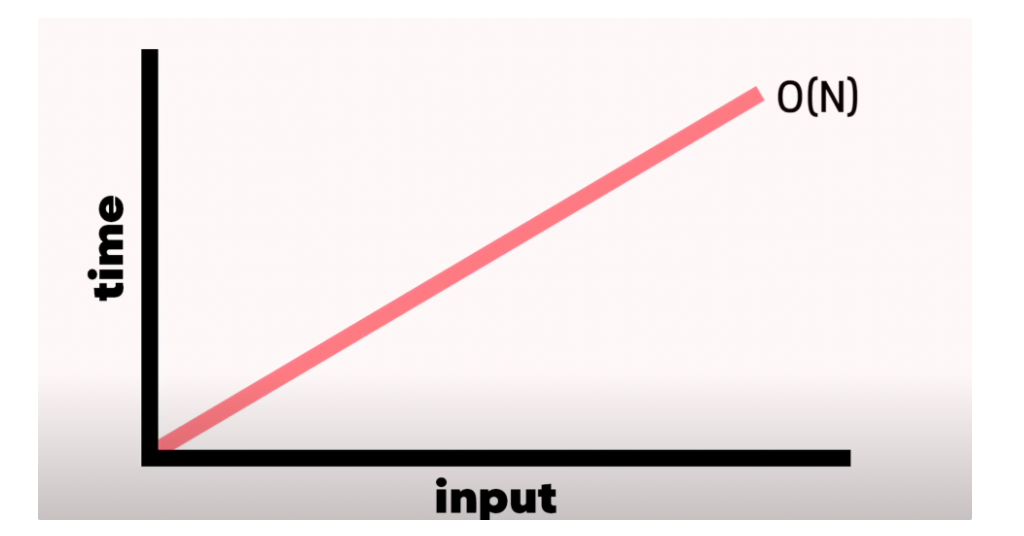
BigO => 0(N)

배열 사이즈가 10이면 10번 출력한다. 배열이 커지면, 필요 스텝도 커진다.

배열의 각각 item을 위해 작업해야 하고 이것은 선형 탐색과 비슷하다.

0(n**2)

2차 시간(Quadratic Time)

ex) 중첩 반복 (Nested Loops)

function print_twice(arr) {
	for (let item of arr) {
		for (let el of arr) {
							console.log(item, el);
	}
 }
}

인풋이 10개라면 100번의 스텝이 필요.

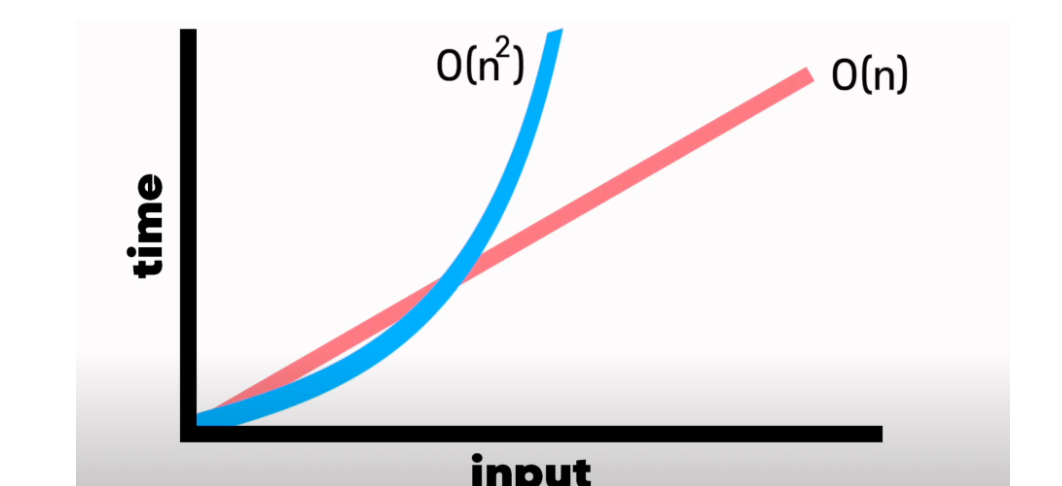
선형 시간복잡도가 더 효율적

O(log n)

로그 시간(Logarithmic Time) : 이진 검색 알고리즘

• 인풋이 10개에서 20개가 되어도 스텝은 + 1 이다. 절반으로 나눠서 진행하기 때문에!
• 로그(logarithm)는 지수(exponent)의 정반대.
• 정렬되지 않은 배열엔 사용 할 수 없다.
  

참조

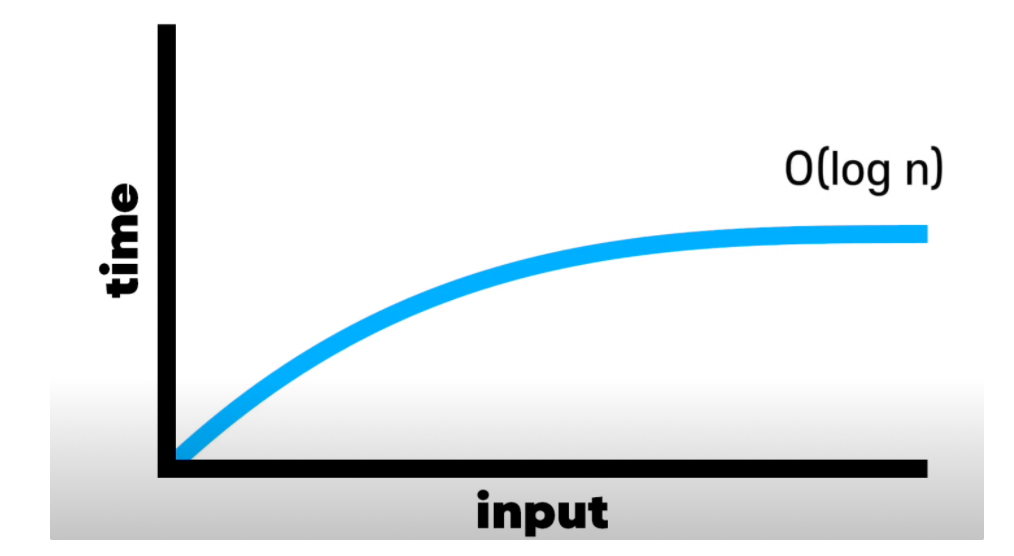
시간복잡도 선호 순위

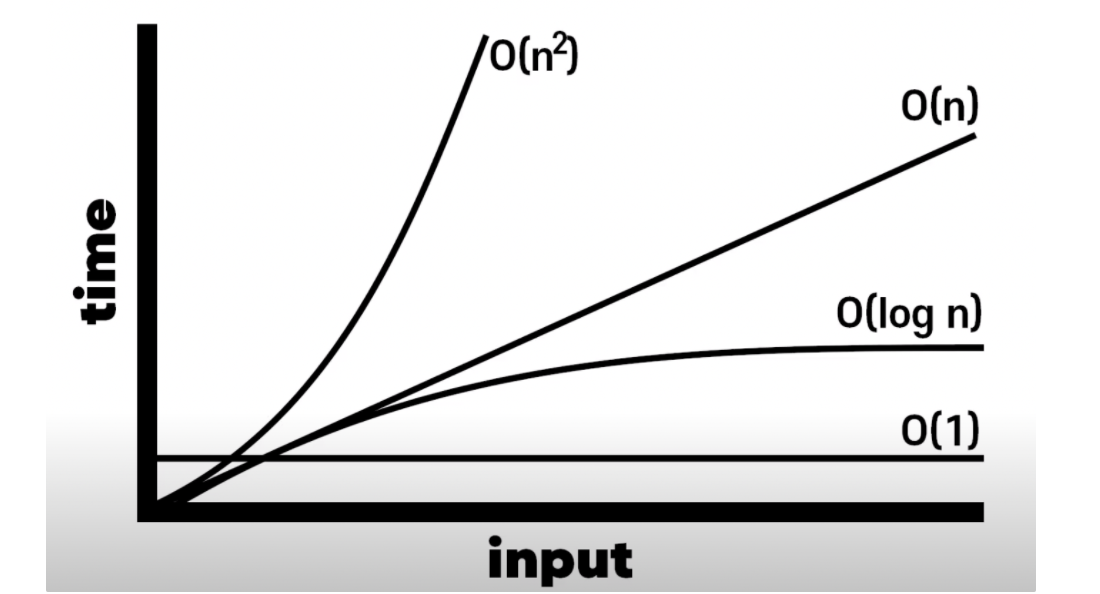
0(1) → 0(log n) → 0(n) → O(n^2)

---

🌲 학습 시작 전 10분 질문 답변 리스트
계획) 오전 질문
📌 오늘 나의 학습 목표는 무엇인가요?
👉 코플릿 자료구조 문제 마무리. 비동기 예습(기본서)

---

🪵 학습 이후 30분 질문 답변 리스트
점검) 데일리 회고 #1/5
📌 오늘 학습 내용 중 새롭게 배운 내용은 무엇인가요?
👉 DFS vs BFS, BigO

점검) 데일리 회고 #2/5
📌 오늘 새롭게 학습한 내용을 다른 사람에게 설명할 수 있나요?
1: 매우 어려움
2: 어려움
3: 보통
4: 가능함
5: 매우 가능함
👉 3

평가) 데일리 회고 #3/5
📌 오늘 학습한 내용 중 아직 이해되지 않은 불확실한 내용은 무엇인가요?
👉 DFS, BFS 코플릿

오류 수정 전략) 데일리 회고 #4/5
이해되지 않은, 불확실한 내용을 보완하기 위해서 나는 무엇을 할 수 있을까요?
👉 매일 매일 조금씩 이해도를 올린다

전체) 데일리 회고 #5/5
📌 나의 오늘 학습 만족도는 몇점인가요?
1: 매우 아쉬움
2: 아쉬움
3: 보통
4: 뛰어남
5: 매우 뛰어남
👉 3