: 모든 정보를 GPU로 보내는 대신 보이는 요소와 보이지 않는 요소를 정렬하고,
보이는 요소만 렌더링하는 최적화 기법

• 평면의 방정식 기법 사용

📒평면의 방정식

---

1. 어떤 벡터와 평면의 노말벡터의 내적이 0이라면 두 벡터는 수직임

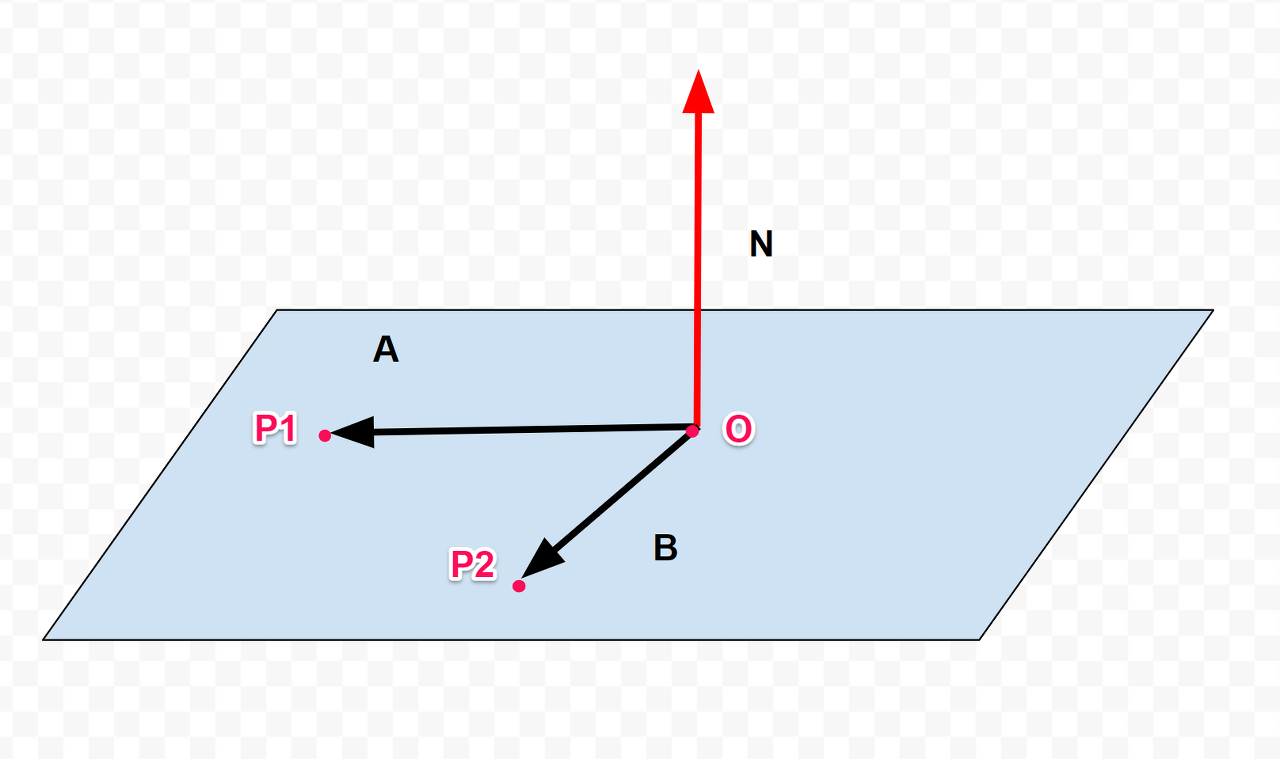
• 수직하는 두 벡터 간의 내적값은 0

  (복습) 내적 Inner Product
  : 투영

  • 각 성분의 합

• 평면 위의 벡터와 평면의 노말벡터는 수직임
  • 평면 위의 벡터: 평면 위의 두 점 사이에 존재하는 방향벡터
• 평면 위의 아무 점들 간 방향벡터와 평면의 노말벡터는 수직임
  • 즉 평면의 방향벡터와 노말벡터의 내적값은 항상 0으로 같음
  • 즉 어떤 벡터와 평면의 노말벡터의 내적이 0이라면 두 벡터는 수직임

2. 원점이 아닌 곳에 존재하는 평면

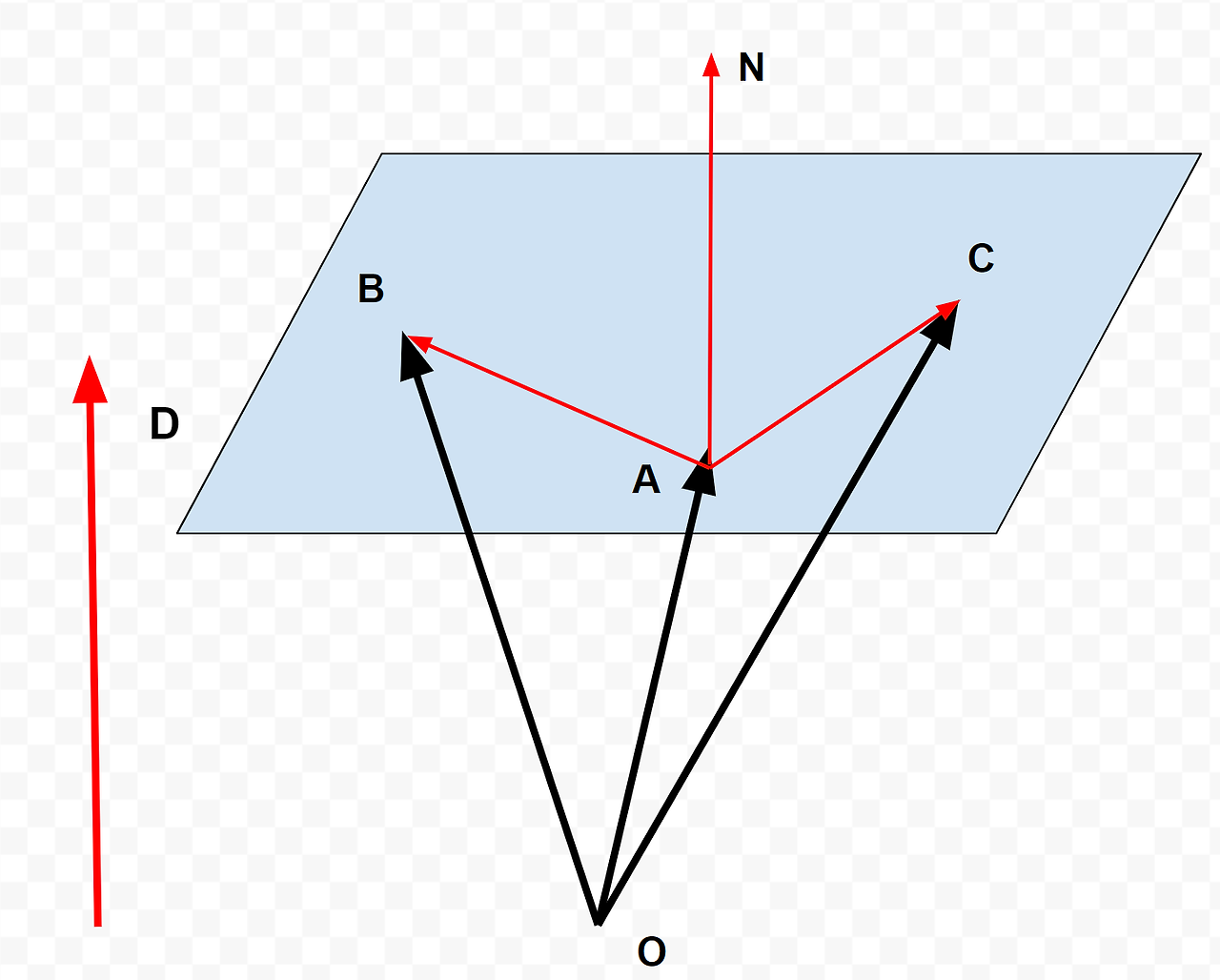
• Normal 판단
  • 평면 위의 방향벡터 V1과, V1의 Tangent vector인 V2까지 두 벡터가 필요함
  • 즉 평면 위의 점 3개가 필요함
• 원점 O로부터 떨어진 거리 D
  • 평면 위의 점을 노멀벡터로 내적하면(투영하면) D의 길이를 구할 수 있음
• 평면의 위치 판단
  • D = 0: 평면이 원점에 위치함
  • D > 0 or D < 0: 평면이 원점에 위치하지 않음
• 평면의 방정식: Ax + By + Cz + D

3. 임의의 정점과 평면

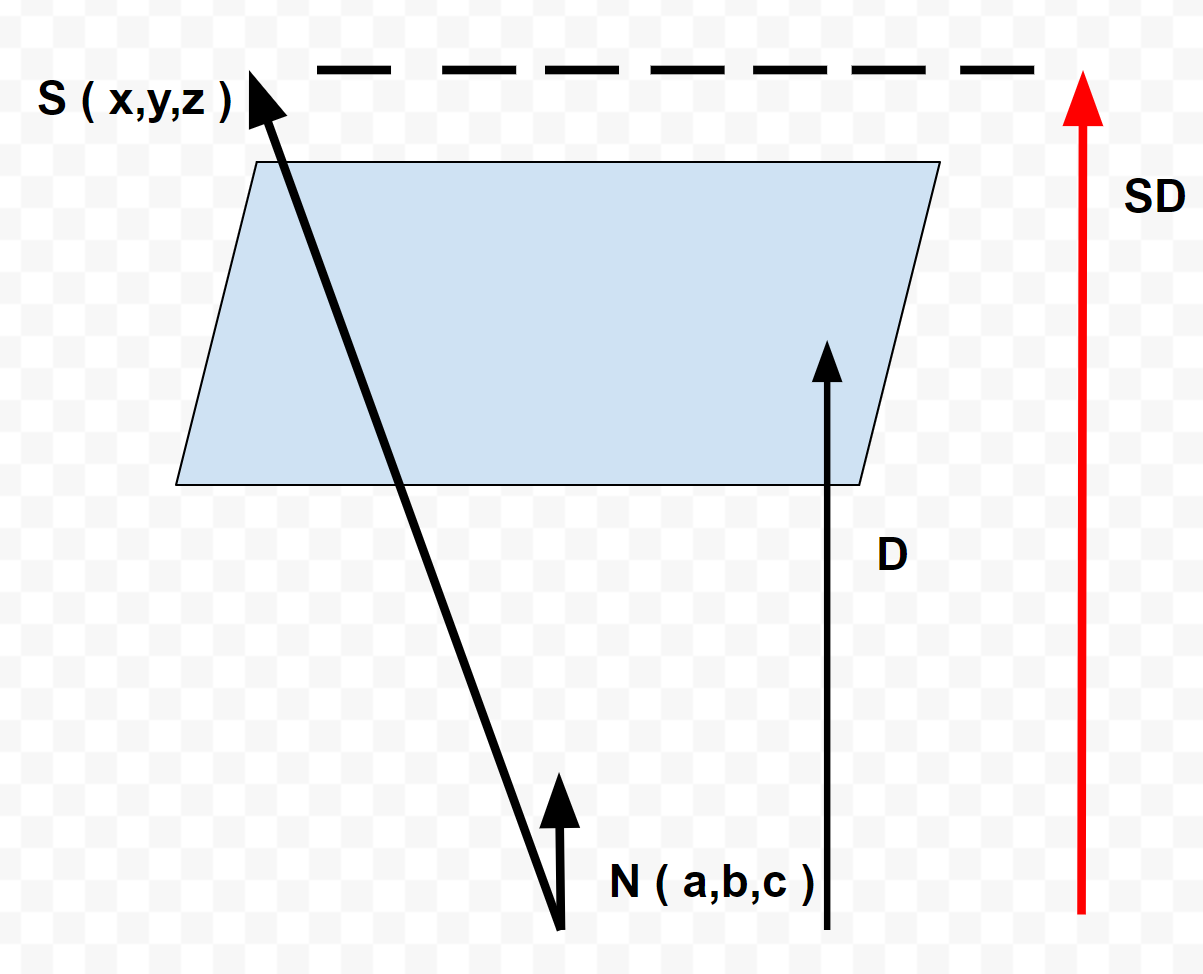
• 임의의 점과 원점 사이의 거리
  • 임의의 점과 평면의 노말벡터를 내적한 값 (자료상 SD)
• 원점으로부터 거리 비교
  • 평면: D
  • 임의의 점: SD
  • 즉, D와 SD를 비교하면 임의의 점이 평면으로부터 떨어진 방향을 구할 수 있음
• 점과 평면의 관계
  • SD > D : 평면 밖
  • SD = D : 평면 위
  • SD < D : 평면 안
• 점과 평면의 방정식
  • 즉, 평면의 방정식을 알고 있다면 대입해서 쉽게 연산 가능
    • 평면의 방정식의 계수를 알고 있다면 내적해서 값 얻을 수 있음
    • 내적: 각 성분의 곱
  • 대입값(내적 + D) > 0 : 평면 밖
  • 대입값(내적 + D) = 0 : 평면 위
  • 대입값(내적 + D) < 0 : 평면 안

📒Frustum Culling

---

: 카메라 시야 범위 즉, 절두체 안에 들어오지 않으면 rendering을 걸지 않는 최적화 방식

• CPU 차원에서 검사

📌절두체 검사

: 절두체의 각 면마다 평면의 방적식 안밖검사, 총 6번 (6면) 검사

• 한 면이라도 통과하지 못하는 경우 카메라에 들어오지 않음
  • 즉 렌더링 않음

📌평면의 방정식 판단

: 평면과 현재 좌표(점)의 관계 연산

• D > P·N : 원점과 평면 사이에 있음
• D = P·N : 평면에 있음
• D < P·N : 원점과 평면 외부에 있음

📌Bounding Box

: 시야각에서 중심은 벗어났지만, 부피가 커서 시야 안에 들어오는 경우

• 문제: 오브젝트의 중심좌표만 체크하는 경우
• 해결: 물체마다 제일 큰 동작 기반으로 벗어남 인정해주는 값 지정

References.
[1] 평면의 방정식: https://m.blog.naver.com/ldj1725/220062476672
[2] Frustum Culling: https://learnopengl.com/Guest-Articles/2021/Scene/Frustum-Culling
[3] Frustum Culling: https://sanghoon23.tistory.com/86