Ridge Regression (with L2 regularization)
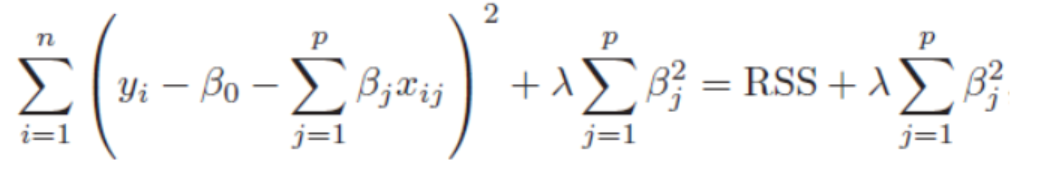
Ridge regression의 식은 Residual Sum of Squares+ penalty (베타 값)의 합으로 이루어져있습니다. 패널티항은 제곱의 형태로 미분이 가능하여 Gradient Descent 최적화가 이루어지고, 파라미터의 크기가 작은 것보다 큰 것을 더 빠른 속도로 줄여주는 효과가 있습니다.
λ(Lambda)가 클수록 coefficients의 estimation은 0으로 가까워 지는 것입니다. 만약 Lambda값이 (λ = 0) 일 때는 패널티 항의 효과가 거의 없어지고, 최소제곱추정치를 생성하게 됩니다.
언제 사용하면 좋을지 (When to use this tool)
기본 선형 모델을 사용하면 종종 Overfitting된 경우 데이터에 매우 적합되어 Variance가 큰 상황을 막기 위하여 coefficient가 크면 페널티를 주는 수식을 추가 한 것이 ridge regression입니다.
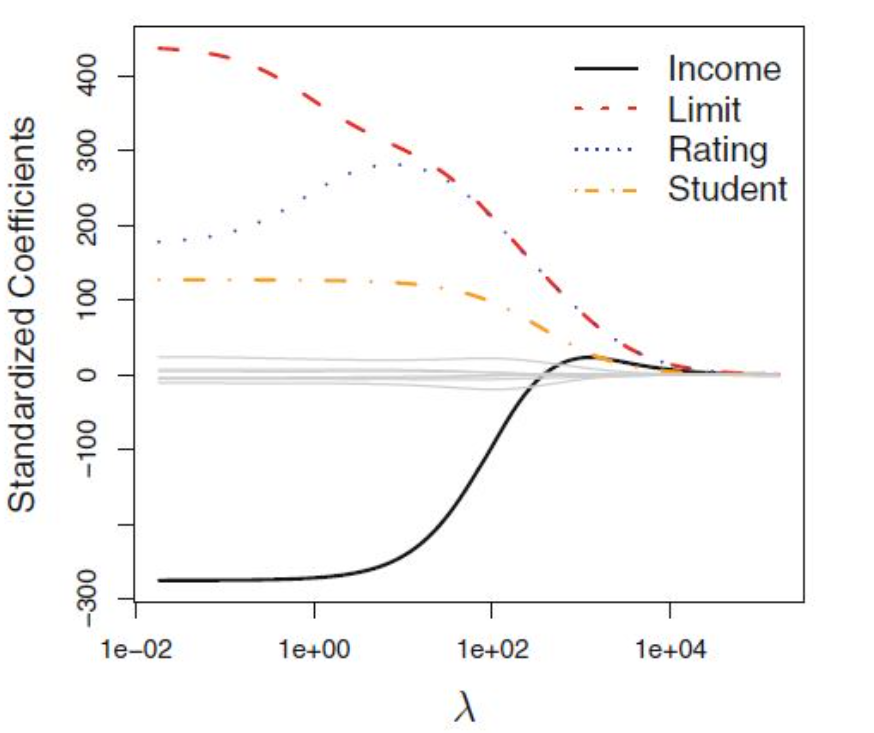
위 그림에서도 확인할 수 있듯이, Lambda가 커질수록 계수를 많이 줄이는데 집중하게 되고,Lambda가 0에 가까워지면 (작아지면) 기존 선형 회귀모델과 같은 최소제곱법 문제가 됩니다. 단, 계수가 0으로 수렴할는 것뿐이지 게수가 0이 되지는 않기 때문에 Lasso와는 다르게 계수를 0으로 만들어 feature selection은 불가능합니다. 즉 정규화의 특성상 Lambda가 클수록, 계수의 크기가 shrink 되는 효과가 생기는 것을 볼 수 있습니다.
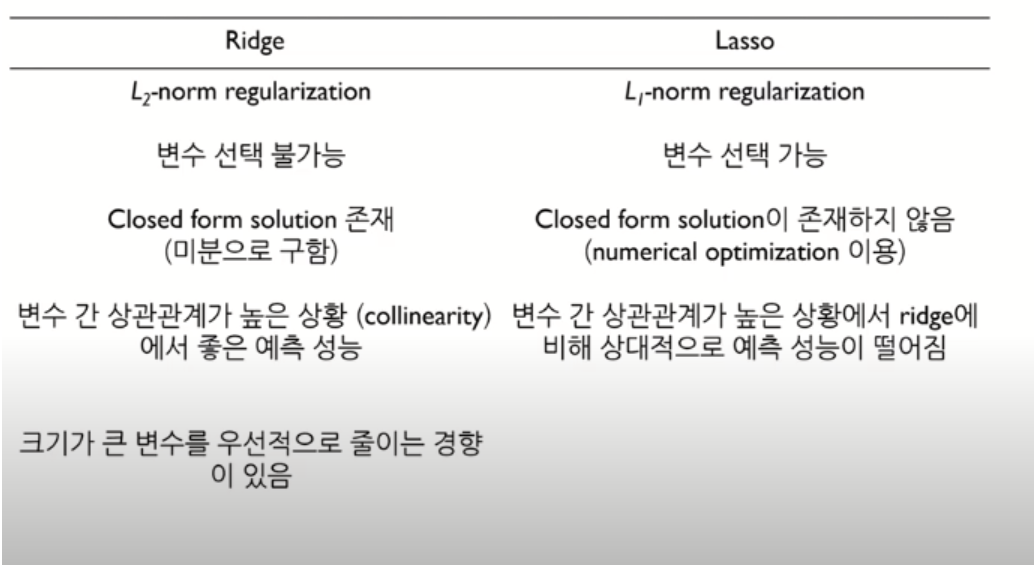
Ridge와 Lasso의 구분
References
https://modern-manual.tistory.com/21
https://rk1993.tistory.com/entry/Ridge-regression%EC%99%80-Lasso-regression-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0
