AR Process
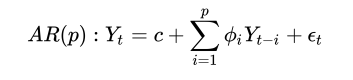AR(1), the first-order AR process
AR(1)의 식에서 coefficient가 1이나 -1이면 random walk의 형태
coefficient>1,coefficient<-1이면 trending의 형태->NON Stationary
AR(2), the second-order AR process
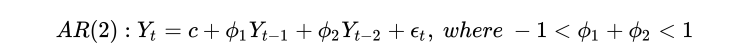
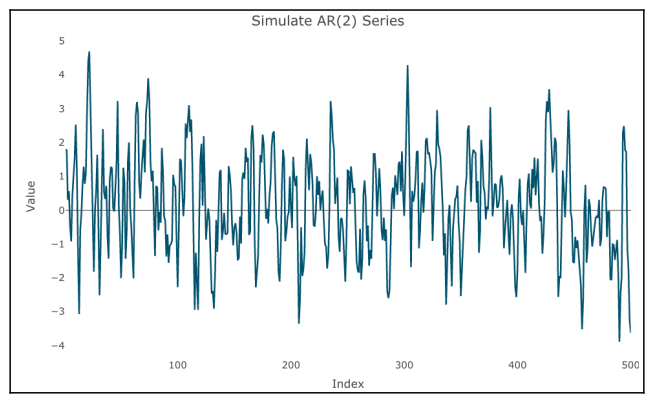
R code example
plot을 적용하면,
ar function R의 stats package에 있는 ar function은 AR모델을 fit해서 coefficient의 값들을 반환해주고 미래의 값들을 예상해줌
Akaike Information Criterion (AIC)을 기반으로 식을 인식하고 최적의 coefficients 제공은 ordinary least squares (OLS), maximum likelihood estimation (MLE), and Yule-Walker에 기반한다.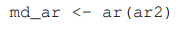 
AutoCorrelation Function (ACF) and Partial Autocorrelation Function (PACF)
ACF는 y(t)와 y(t+k)사이의 자기 상관을 구하는 것으로
정상시계열의 경우 상대적으로 빠르게 0에 수렴하는 형태이고
비정상시계열의 경우 천천히 감소하고, 큰 양의 값을 가짐
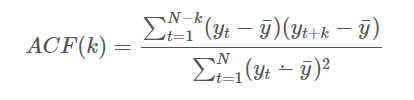
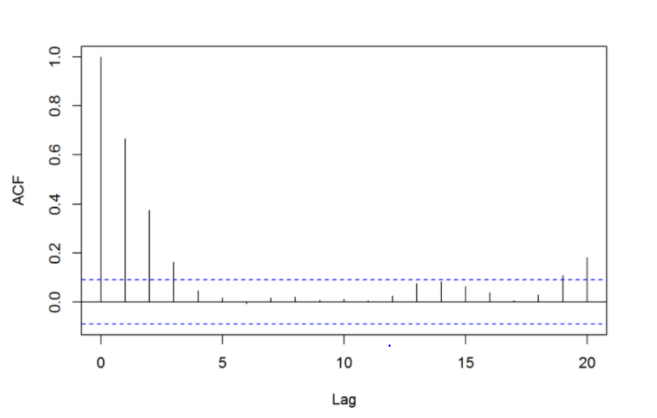위 그래프의 경우 파란색 선 위가 유의미한 값들을 의미하기 때문에 lag3까지 유의한 값들을 가진다. 그러므로 ARIMA 모델에서 계수인 p=3으로 예상할 수 있다.
PCAF는 시차에 따른 편자기상관계이고 다른 모든 짧은 시차 항에 따라 조정한 후 k 시간 단위로 구분된 시계열(yt–1, yt–2, ..., yt–k–1)의 관측치(yt 및 yt–k) 간 상관의 측도이다.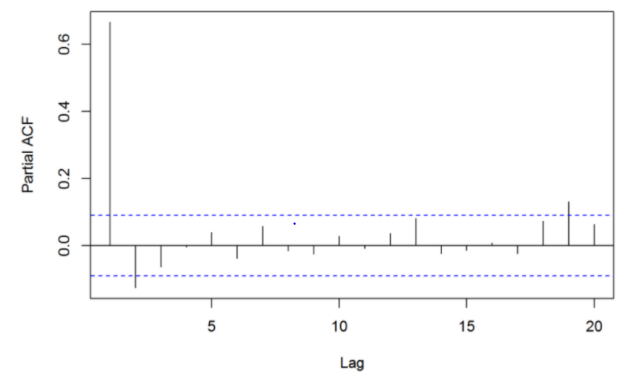
위의 그래프의 경우 계수를 2로 예상할 수 있다.
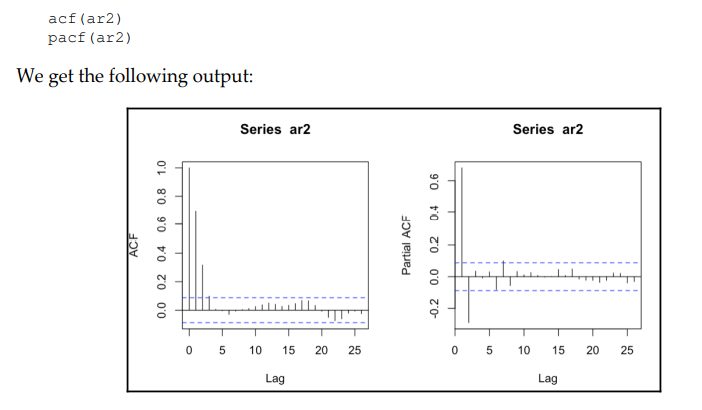분석:
Correlation Analysis, allows us to classify the process
type and identify its order. If the ACF output tails off and the PACF output cuts off at lag p, this indicates that the series is an AR(p) process.
References
