Stationary 시계열
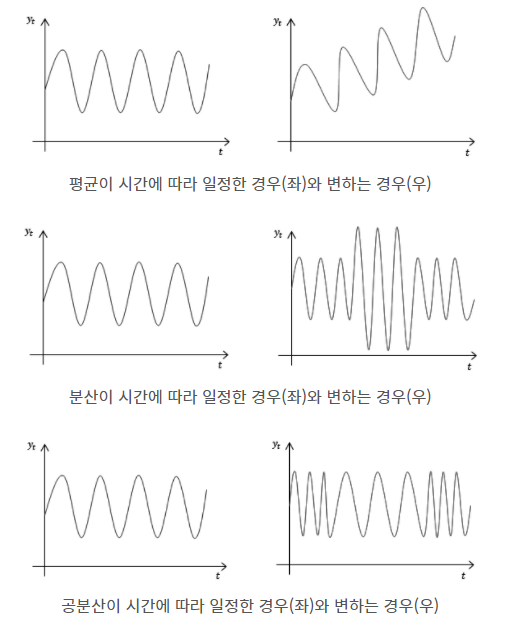
: 시간의 추이와 관련 없이 일정한 평균과 분산을 가짐
대부분의 시계열 자료가 일정한 평균과 분산을 가지고 있지 않는 NON- Stationary 자료이기 때문에 분석하기 쉬운 Stationary time series형태로 변환하는 작업이 필요함
평균이 일정하지 않는 경우는 대개 differencing, 분산이 일정하지 않는 경우는 transformation 과정 수반
* Differencing 차분에 의한 계절성 효과 제거:
매달 측정되는 시계열 데이터의 경우에는 계절성 효과가 흔하기 때문에 differencing을 이용한 계절성을 제거하고 잠재적인 trend도 제거 가능
'''
차분(differencing)은 시계열의 수준에서 나타내는 변화를 제거하여 시계열의 평균 변화를 일정하게 만드는 역할
'''

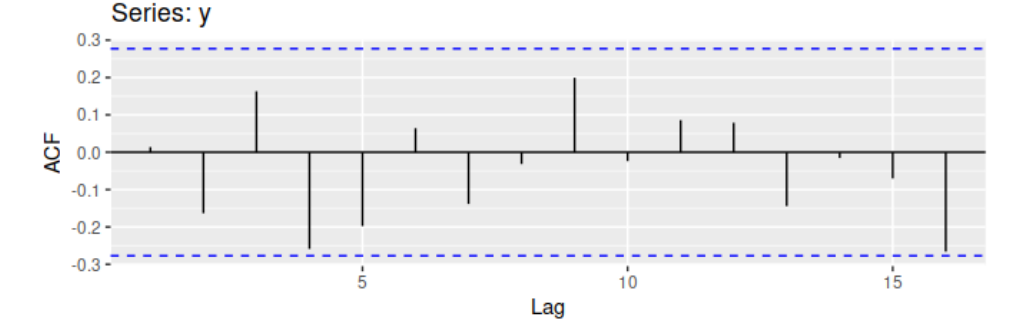
Autocorrelation(자기 상관)
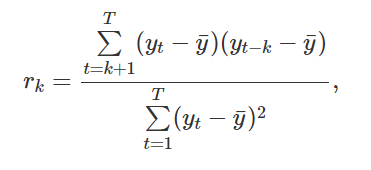
*자기상관(autocorrelation)은 시계열의 시차 값(lagged values) 사이의 선형 관계를 측정
r(k)는 y(t)와 y(t-k) 사이의 관계를 측정하는 식
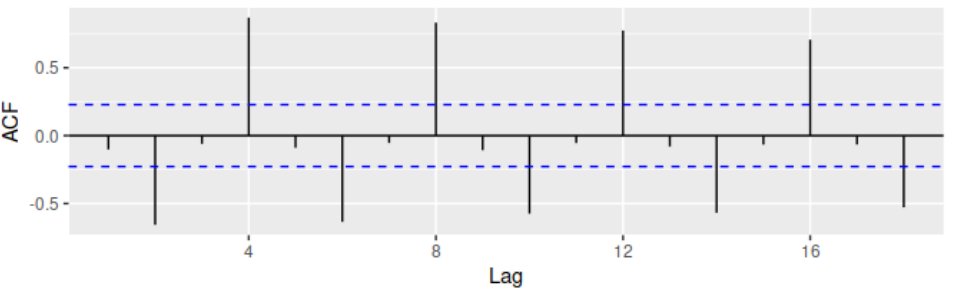
위의 그래프는 자기상관함수(ACF)를 나타내기 위한 것으로 r(4)는 다른 시차들의 계절성 패턴으로 다른 기준치보다 높은 ACF를 보이고 있음.
White noise: Stationary example
white noise(백색 잡음)은 시간에 상관없이 평균이 0이고 분산은 σ^2임을 가정. 즉, 자기상관(autocorrelation)이 없는 경우를 일컫음.
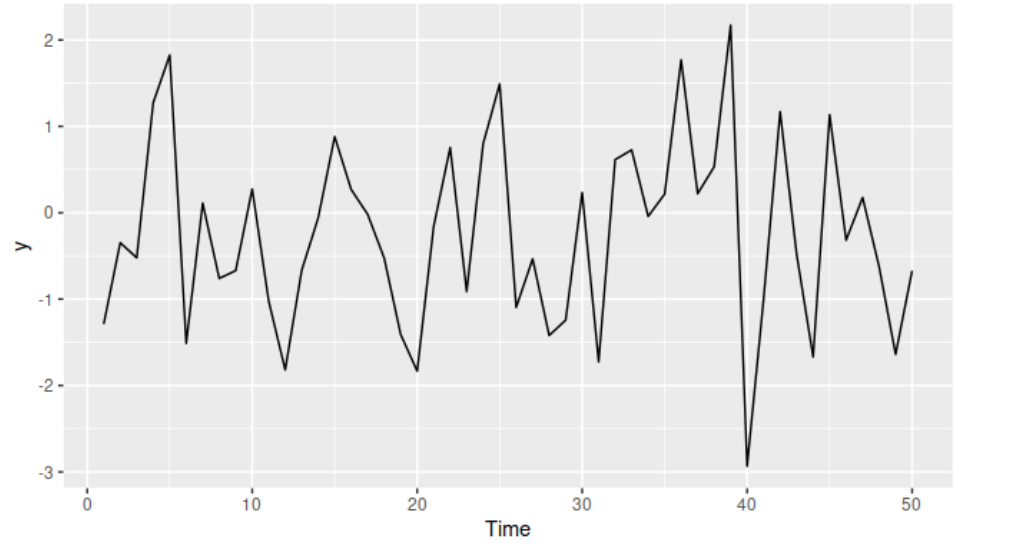
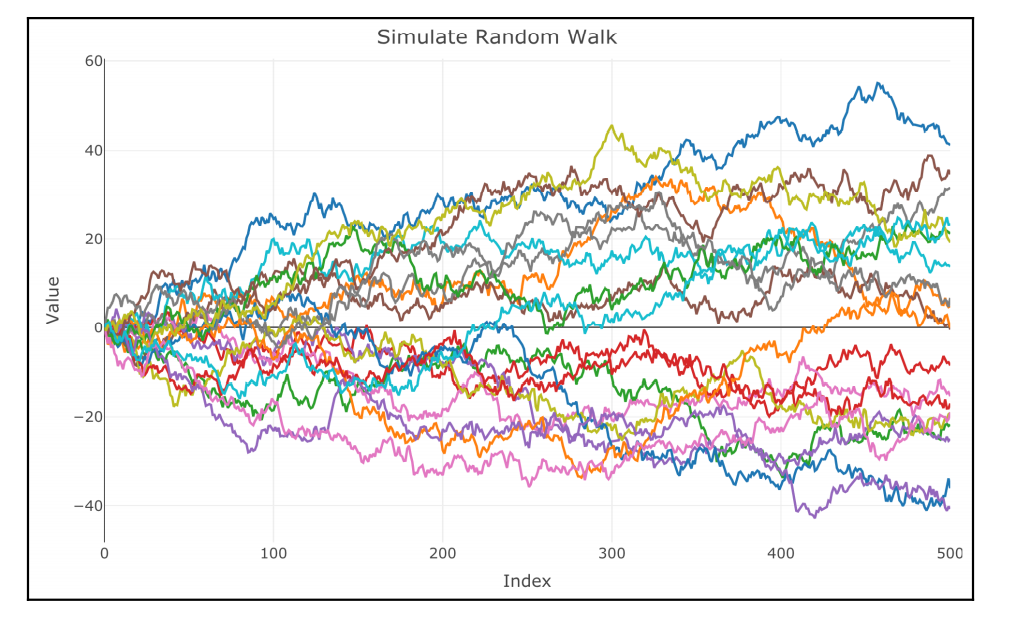
Random Walk (확률 보행): Non Stationary example
Random walk는 임의의 방향으로 향하는 연속적인 걸음을 나타낸다는 의미로 예측 불가능한 변동이 발생하는 것을 뜻함-> NON Stionary
위로갈 확률이나 아래로갈 확률이 같아서 미래 이동을 아예 예측할 수 없기 때문에 확률보행 모델에서 예측값은 마지막 예측값과 같다고 가정함
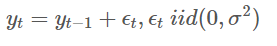
References
https://velog.io/@cha-suyeon/%EC%8B%9C%EA%B3%84%EC%97%B4-%EB%8D%B0%EC%9D%B4%ED%84%B0-%EC%A0%95%EC%83%81%EC%84%B1Stationarity-%EC%B0%A8%EB%B6%84differencing-%ED%99%95%EB%A5%A0%EB%B3%B4%ED%96%89-2%EC%B0%A8-%EC%B0%A8%EB%B6%84
https://books.google.co.kr/books/about/Hands_On_Time_Series_Analysis_with_R.html?id=F9KytQEACAAJ&redir_esc=y
https://otexts.com/fppkr/wn.html
https://syj9700.tistory.com/26
R 응용 시계열분석 (저자:나종화)
