BFS DFS
BFS DFS
그래프에서 모든 정점을 방문해야는 방법 중 가장 대표적인 것은
너비 우선 탐색(BFS) 와 깊이 우선 탐색(DFS) 이다.
다음의 사진들은 트리를 대상으로 각각 BFS, DFS 를 적용한 것이다.
너비 우선 탐색
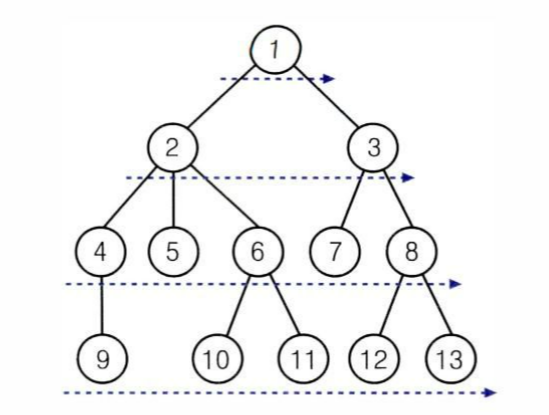
BFS는 루트를 시작으로 탐색을 시작하면 먼저 루트의 자식을 차례대로 반복한뒤
루트 자식의 자식으로, 즉 루트에서 두 개의 간선을 거쳐서 도달할 수 있는 정점을 방문한다.
1 -> (2,3) -> (4,5,6,7,8)
BFS는 루트에서 거리 순으로 방문한다.
깊이 우선 탐색
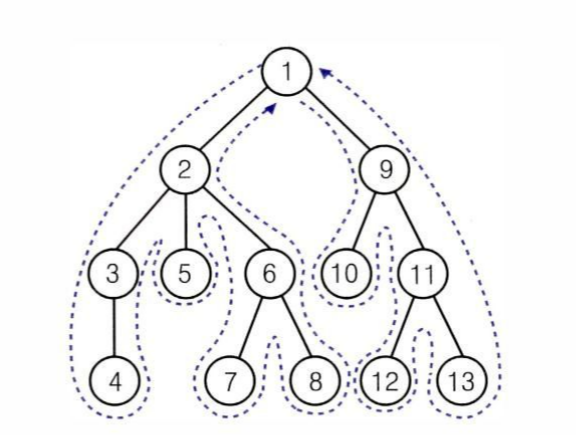
DFS는 루트의 자식 정점 하나를 방문한 다음 아래로 내려갈 수 있는 곳까지 내려간다.
더 이상 내려갈 수가 없으면 위로 되돌아오다가 내려갈 곳이 있으면 즉각 내려간다.
1 -> 2 -> 3 -> 4 -> 5.....
일반적인 그래프 G=(V,E)에 대한 BFS, DFS는 다음과 같다.
너비 우선 탐색
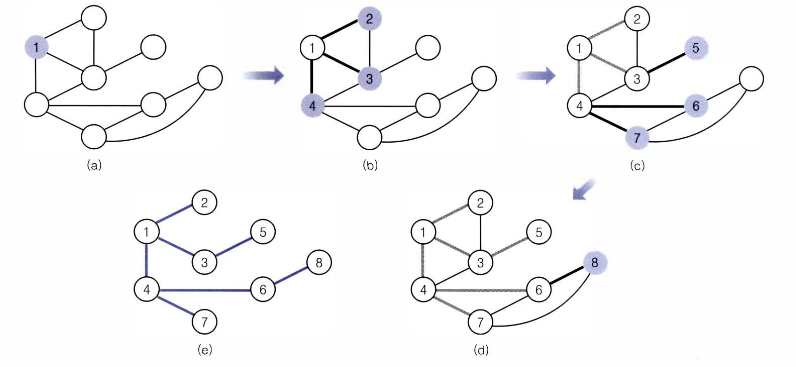
BFS는 인접한 정점에 해당하는 정점을 모두 탐색한뒤
탐색한 정점과 인접하지만 탐색하지 않았던 정점을 탐색하는것을 반복한다.
깊이 우선 탐색
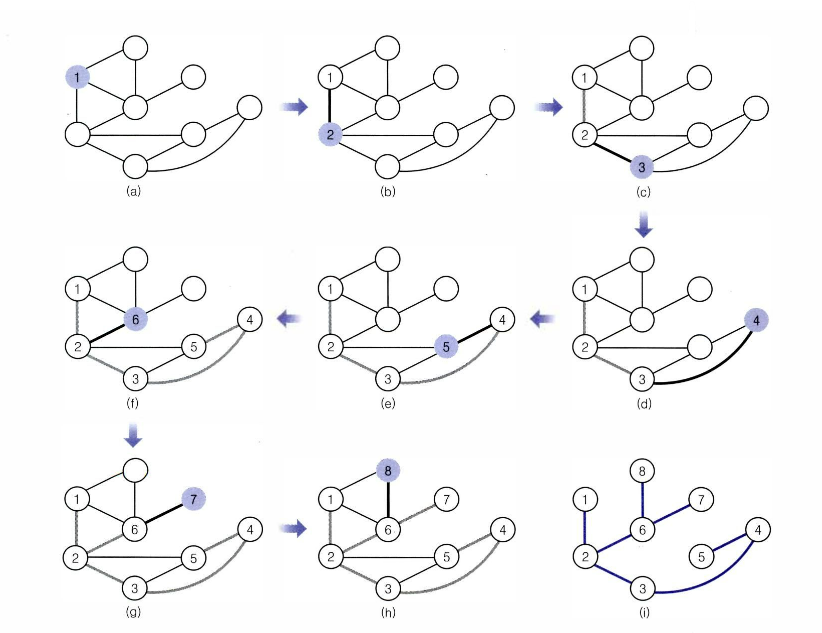
DFS는 인접한 정점 중 하나를 선택해서 해당하는 정점의 끝까지 탐색하고 되돌아오는것을 반복한다.
그림 (b),(c),(d)에서 각각 인접한 다른 정점들이 존재하는데 이런 경우에는 자유롭게 원하는 정점을 선택해 방문해 주면 된다.
BFS 알고리즘
BFS(G,s)
{
for each v ∈ V-{s}
visited[v] <- NO;
visited[s] <- Yes; // s: 시작 정점
enqueue(Q,s);(처음엔 1값만 가져옴) // Q:큐, Q에서 s값을 읽어옴
while (Q!=ø) {
u <- dequeue(Q); // Q값을 출력하여 u에 저장함
for each v ∈ L(u) // L(u) : 정점 u의 인접 정점 집합
if (visited[v] = NO) then{
visited[v] <- YES;
enqueue(Q,v);
}
}
}
-
V-{s}에 해당하는 모든 정점에 visited[v] <- NO;
시작 정점으로 쓰일 첫 정점값만 visited[s] <- Yes; -
Q가 공집합이 아닐때까지 즉 모든 정점이 visited[v] <- Yes;가 될때까지
while문 반복 -
q값 출력해서 u에 담고 u의 인접 정점 집합인 L(u)의 원소인 v에대해
visited[v] = NO 라면 visited[v] <- YES; 로 바꾸고
Q에서 v값을 가져온다.BFS의 수행 시간은 O(V+E)이다. V = 정점, E = 간선
DFS 알고리즘
DFS(v)
{visited[v] <- YES; for each x ∈ L(v) //L(v): 정점 v의 인접 정점 집합 if (visited[x] = NO) then DFS(x);}
-
정점 v를 visited[v] <- YES; 처리한다
-
이와 인접한 정점(for each x ∈ L(v))중 visited[x] = NO 인 정점이 있다면
-
다시 DFS 함수를 호출한다.
DFS의 수행 시간은 O(V+E)이다. V = 정점, E = 간선
위의 BFS,DFS는 모두 연결 그래프를 가정한 것이다.
만일 분리된 두 개 이상의 부분 그래프가 있다면
BFS나 DFS를 부분 그래프의 수만큼 수행해야 모든 정점을 방문할 수 있다.연결 그래프가 아닌 DFS의 알고리즘
DFS(G)
{for each v ∈ V visited[v] <- NO; for each v ∈ V if(visited[v] <- NO) then aDFS(v);}
aDFS(v)
{visited[v] <- YES; for each x ∈ L(v) //L(v): 정점 v의 인접 정점 집합 if (visited[x] = NO) then aDFS(x);
}
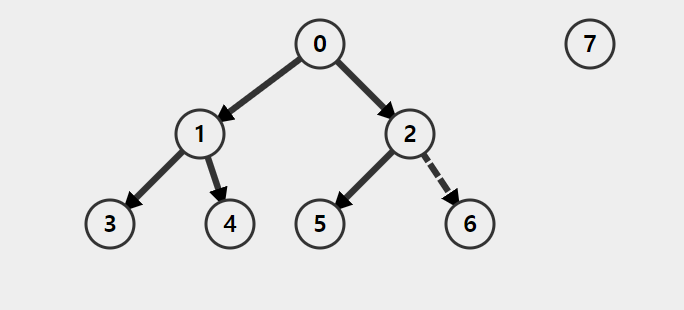
연결 그래프가 아닌 그래프
출처: 쉽게 배우는 알고리즘