최단 경로 알고리즘
최단 경로 문제에서 입력 그래프의 유형은 크게 두 가지로
모든 간선의 가중치가 음이 아닌 다익스트라 알고리즘
음의 가중치가 존재하는 벨만-포드 알고리즘이 있다.
오늘은 이 중에서 다익스트라 알고리즘만 알아보려고 한다.
Dijstra
다익스트라 알고리즘은 사이클이 없는 그래프이기 때문에,
하나의 시작 정점에서 다른 모든 정점까지 최단 경로를 구한다.
따라서 (n-1)개의 경로를 구하게 된다.
이와 같은 유형을 단일 시작점 최단 경로 문제 라고 한다.
해당 알고리즘에서는
임의의 두 정점간의 경로가 존재하지 않으면 해당 경로의 길이는 ∞로 정의하고
두 정점 사이에 간선이 없으면 가중치가 ∞인 간선이 있다 간주한다.
다익스트라 그래프
---
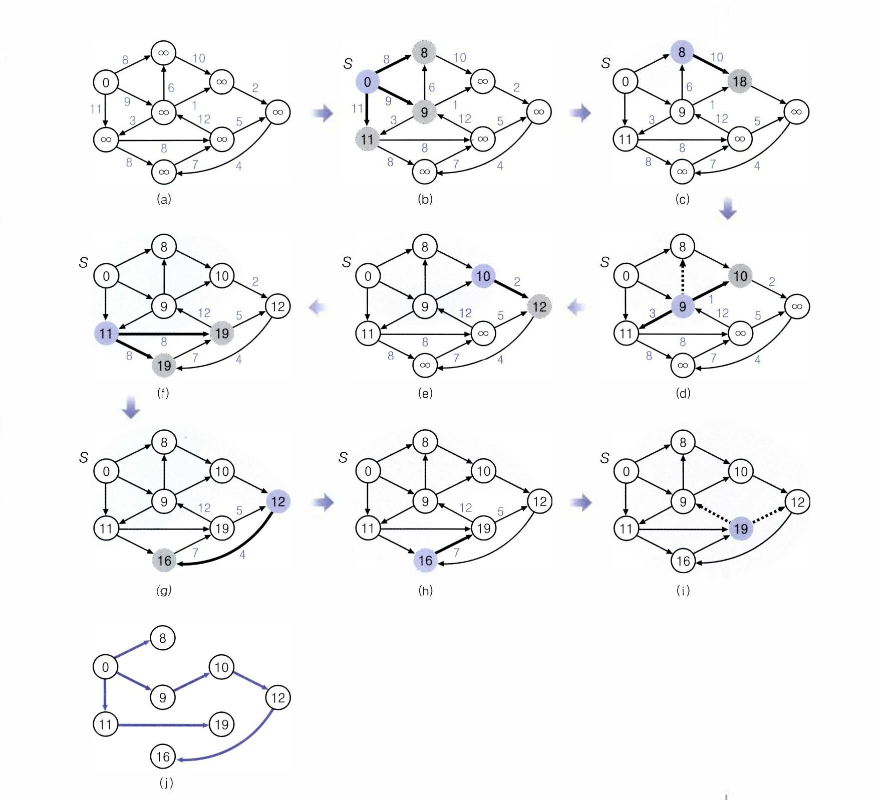
- 시작 정점 r만 최단 거리 0으로 초기화하고 다른 정점들의 최단 거리는 모두 ∞로 초기화 한다.
- 정점 r을 집합 S의 첫번째 원소로 포함시키고 집합 S 즉 현재 r과 인접한 3개의 정점에 해당하는 곳을 각각 ∞에서 해당 정점에 도달할때의 최단거리값
즉 각각 (8,9,10)으로 값을 바꿔준다.
하지만 회색 상태는 값만 바뀐것이고 S집합에 포함시키는것은 아니다.
이들중 가장 거리가 가까운 8을 집합 S에 포함시켜준다.
- 집합 S에 8을 포함시키자, 8과 인접한 정점의 최단거리 역시 ∞에서 18로 바뀌었다.
이 상태에서 S와 인접한 정점들의 최단거리값은 각각 (9,10,18)이 된다.
따라서 9를 집합 S에 포함시켜준다.
- 집합 S에 9가 추가되면서 최단거리값이 18에서 10으로 바뀌었고
이 상태에서 최단거리값은 (10, 11)이 된다.
따라서 10을 집합 S에 포합시켜준다.
- 집합 S에 10이 추가되면서 새로운 정점이 ∞에서 12로 최단거리값이 변경되었다.
이 상태에서 최단거리값은 (11,12)이므로 11을 집합 S에 포함시킨다.
- 집합 S에 11이 추가되면서 새로운 2개의 정점이 각각 ∞에서 19로 최단거리값이 변경되었다.
이 상태에서 최단거리값은 (12,19,19)이므로 12를 집합 S에 포함시킨다.
- 집합 S에 12가 추가되면서 한개의 정점이 19에서 16으로 최단거리 값이 변경되었다.
집합 S에 16을 포함시키고 그뒤에 19을 포함시키며 마무리된다.
다익스트라 알고리즘
Dijstra(G,R)
G=(V,E): 주어진 그래프
r: 시작으로 삼을 정점
{
S <- ∅; // S: 정점 집합
for each u∈V // 정점 r에서부터 정점 u에 이르는 최단거리
d[u] <- ∞; // 최단이기에 ∞사용, 최장거리 계산시에는 -∞
d[r] <- 0;
while (S!=V){
u <- extractMin (V-S,d); //제일작은 값을 주는데, d[r]<-0;이므로 r을 주게된다
S <- S∪{u};
for each v∈L(u) //L(u): 정점 u로부터 연결된 정점들의 집합
if( v ∈ V-S and d[u] + w(u,v) < d[v])then{ //최단거리 교체용 if문 d[u] = 최단경로(**그림설명**)
d[v] <- d[u] + w(u,v); //최단경로 수정
prev[v] <- u; //삽입
}
}
}
extractMin(Q,d[])
{
집합 Q에서 d값이 가장 작은 정점 u를 리턴한다; //d=최단거리
}
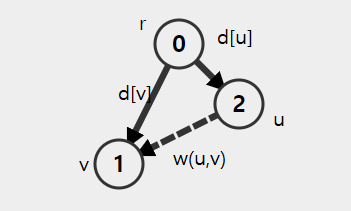
추가설명
if( v ∈ V-S and d[u] + w(u,v) < d[v])then
v ∈ V-S 를 만족할때
d[u] + w(u,v) < d[v]이면 밑줄의 최단경로 수정으로 이동
r에서 v라는 정점으로 바로 이동할때 거리가 d[v]인데
r에서 u라는 다른 정점으로 이동할때 거리 d[u] + u에서 v로 이동할때의 거리를 합한 거리 w(u,v)가
d[v]보다 짧다면 d[v]값을 d[u] + w(u,v)로 변경한다는 내용이다.
위의 다익스트라 그래프에서 (c) -> (d) 과정이 이 과정을 통해 바뀐 것이다.
수행시간
다익스트라 알고리즘의 수행시간은 힙을 이용하면 O(ElogV)이다.
출처: 쉽게 배우는 알고리즘
