기본적인 정렬 알고리즘
-
기본적인 정렬 알고리즘
선택정렬
버블정렬
삽입정렬
선택 정렬
선택 정렬은 원리가 간단한 정렬 알고리즘이다.
배열 A[1 . . . n]에서 가장 큰 원소를 찾아 이원소와 배열의 끝자리에 있는
A[n]과 자리를 바꾼다.
해당 원소는 정렬이 완료되었으므로 다음작업에서는 해당 원소를 제외한
나머지 원소들로 같은 동작을 반복한다.선택정렬의 수행 시간은 (n-1)+(n-2)+...+2+1 = n(n-1)/2 이므로 항상 O(n^2)이다.
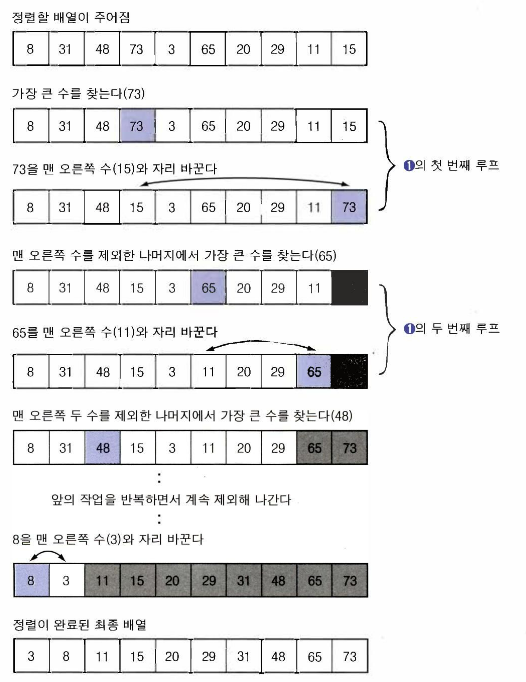
선택 정렬 알고리즘
selectionSort(A[],n)
{
for last <- n downto 2{ // downto 는 to의 반대 4 downto 1 = 1234
k <- theLargest(A, last);
A[k] ↔ A[last]; // A[k]와 A[last]의 값 교환
}}
theLargest(A[],last)
{
largest <- 1;
for i <- 2 to last
if (A[i] > A[largest]) then largest <- 1;
return largest;}
파이썬을 이용한 선택 정렬 구현
def selection_sort(arr):
for i in range(len(arr) - 1):
min_idx = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]자바를 이용한 선택 정렬 구현
public class Selection {
public static void sort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIdx = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIdx])
minIdx = j;
}
swap(arr, i, minIdx);
}
}
private static void swap(int[] arr, int a, int b) {
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
}버블 정렬
버블 정렬의 원리도 선택 정렬과 크게 다르지않다.
제일 큰 원소를 끝자리로 옮기는 작업을 반복하는 것이다.
차이점은 제일 큰 원소를 오른쪽으로 옮기는 방식이다.
선택정렬은 last와 제일 큰 원소의 위치를 바꾸는 방식이지만
버블 정렬은 왼쪽부터 오름차순으로 비교해가며 순서에 맞지않으면 서로 위치를 바꾼다.
이를 반복하면 처음 오른쪽 끝에 도달했을때 제일 큰 숫자가 last위치에 오게된다.
버블 정렬의 수행시간도 선택 정렬과 마찬가지로 (n-1)+(n-2)+...+2+1 = n(n-1)/2 이므로 항상 O(n^2)이다.
하지만 개선된 버블 정렬을 이용하면 정렬이 되어있는 경우에 최선의 수행시간이 O(n)이 된다.
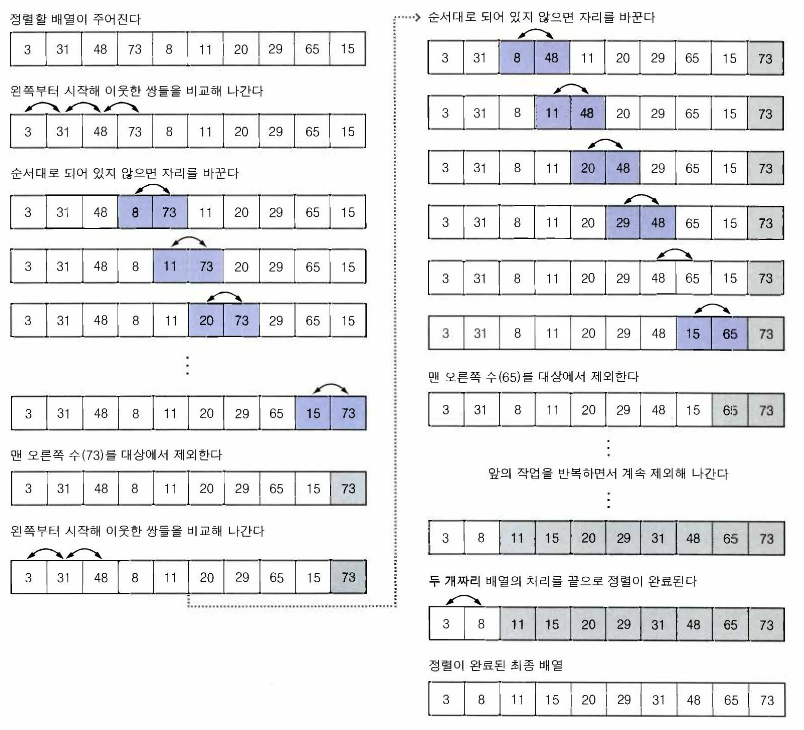
버블 정렬 알고리즘
bubbleSort(A[], n)
{
for last <- n downto 2
for i to last-1
if (A[i] > A[i+1]) then A[i] ↔ A[i+1];}
- 개선된 버블 정렬 알고리즘
bubbleSort(A[], n)
{
for last <- n downto 2
sorted <- TRUE;
for i to last-1{
if (A[i] > A[i+1]) then A[i] ↔ A[i+1];
sorted <- FALSE;
}
if(sorted = TRUE) then return;
}}
파이썬을 이용한 버블 정렬 구현
def bubble_sort(arr):
for i in range(len(arr) - 1, 0, -1):
for j in range(i):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]자바를 이용한 버블 정렬 구현
public class Bubble {
public static void sort(int[] arr) {
for (int i = arr.length - 1; i > 0; i--) {
boolean swapped = false;
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
swapped = true;
}
}
if (!swapped) break;
}
}
private static void swap(int[] arr, int a, int b) {
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
}삽입 정렬
삽입 정렬은 이미 정렬되어 있는 i개짜리 배열에 하나의 원소를 더 더하여
정렬된 i+1개짜리 배열을 만드는 과정을 반복한다.
선택 정렬과 버블 정렬이 n개 짜리 배열 에서 아직 정렬되지 않은 배열의 크기를 하나씩 줄이는 데 반해
삽입 정렬은 한 개 짜리 배열에서 시작해서 이미 정렬된 배열의 크기를 하나씩 늘리는 정렬이다.
삽입 정렬의 수행시간은 1+2+3+...+(n-1) = n(n-1)/2 이므로 O(n^2) 이지만
배열이 완전히 정렬되어 있다면 while 루프를 한 번도 수행하지 않아 최적의 수행시간은 O(n) 이된다.
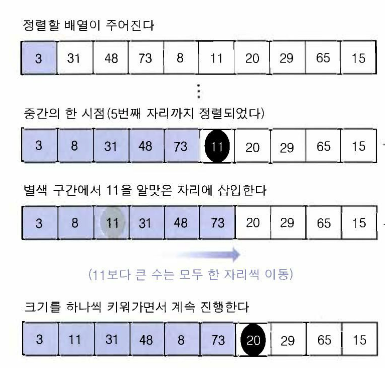
삽입 정렬 알고리즘
insertionSort(A[],n)
{
for i <- 2 to n {
loc <- i-1;
newItem <- A[i]; // 이 지점에서 A[1~i-1]은 정렬되어있는 상태
while ( loc >= 1 and newItem < A[loc]) {
A[loc+1] <- A[loc];
loc--; // newItem과 loc를 하나씩 비교하며 마지막엔 탈출
}
A[loc+1] <- newItem; //while문을 거치지 않는 경우 맨앞에 추가
}}
파이썬을 이용한 삽입 정렬 구현
def insertion_sort(arr):
for end in range(1, len(arr)):
for i in range(end, 0, -1):
if arr[i - 1] > arr[i]:
arr[i - 1], arr[i] = arr[i], arr[i - 1]자바를 이용한 삽입 정렬 구현
public class Insertion {
public static void sort(int[] arr) {
for (int end = 1; end < arr.length; end++) {
int toInsert = arr[end];
int i = end;
while (i > 0 && arr[i - 1] > toInsert) {
arr[i] = arr[i - 1];
i--;
}
arr[i] = toInsert;
}
}
}출처 - 쉽게 배우는 알고리즘
https://www.daleseo.com/sort-selection/
https://www.daleseo.com/sort-bubble/
https://www.daleseo.com/sort-insertion/
