1. 개요

• 
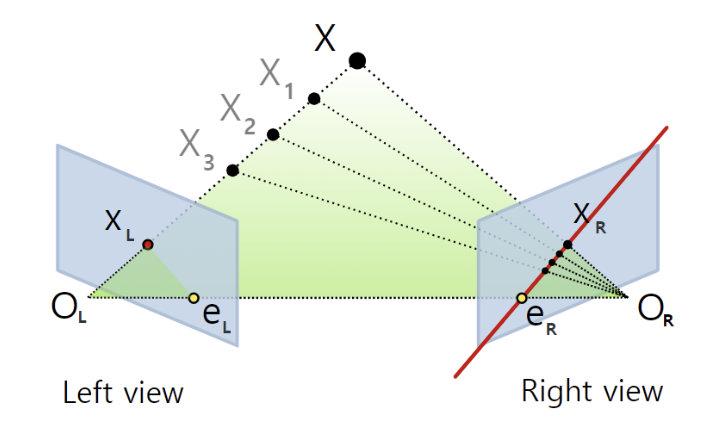
• 위 그림은 2개의 카메라 원점(OL, OR)에서 촬영된 이미지(파란색평면) 내 점(XL, XR)과 3차원 점(X)간의 관계를 표현하는 그림
• Epipolar Geometry의 목적
  • 예시1) 2개 이미지 내 동일 점의 위치, 카메라 intrinsic/extrinsic prameter를 알면
    • 3D Point의 좌표를 계산 할 수 있습니다.
  • 예시2)
    • 2개 카메라 intrinsic/extrinsic parameter가 주어진다면,
      • left view에서 점XL은 right view의 XR~eR를 잇는 선위에 위치하게 됩니다.
      • left view에서 XL의 깊이를 알 수 없기 때문입니다.
      • 이를 수행해주는 변환 행렬이 Essential matrix / Fundamental Matrix
  • 예시3)
    • 2개 이미지 내 동일점의 위치 8개만 주어지면,
      • 2개 이미지간의 변환관계 matrix를 계산 할 수 있습니다.

2. Essential Matrix

• 
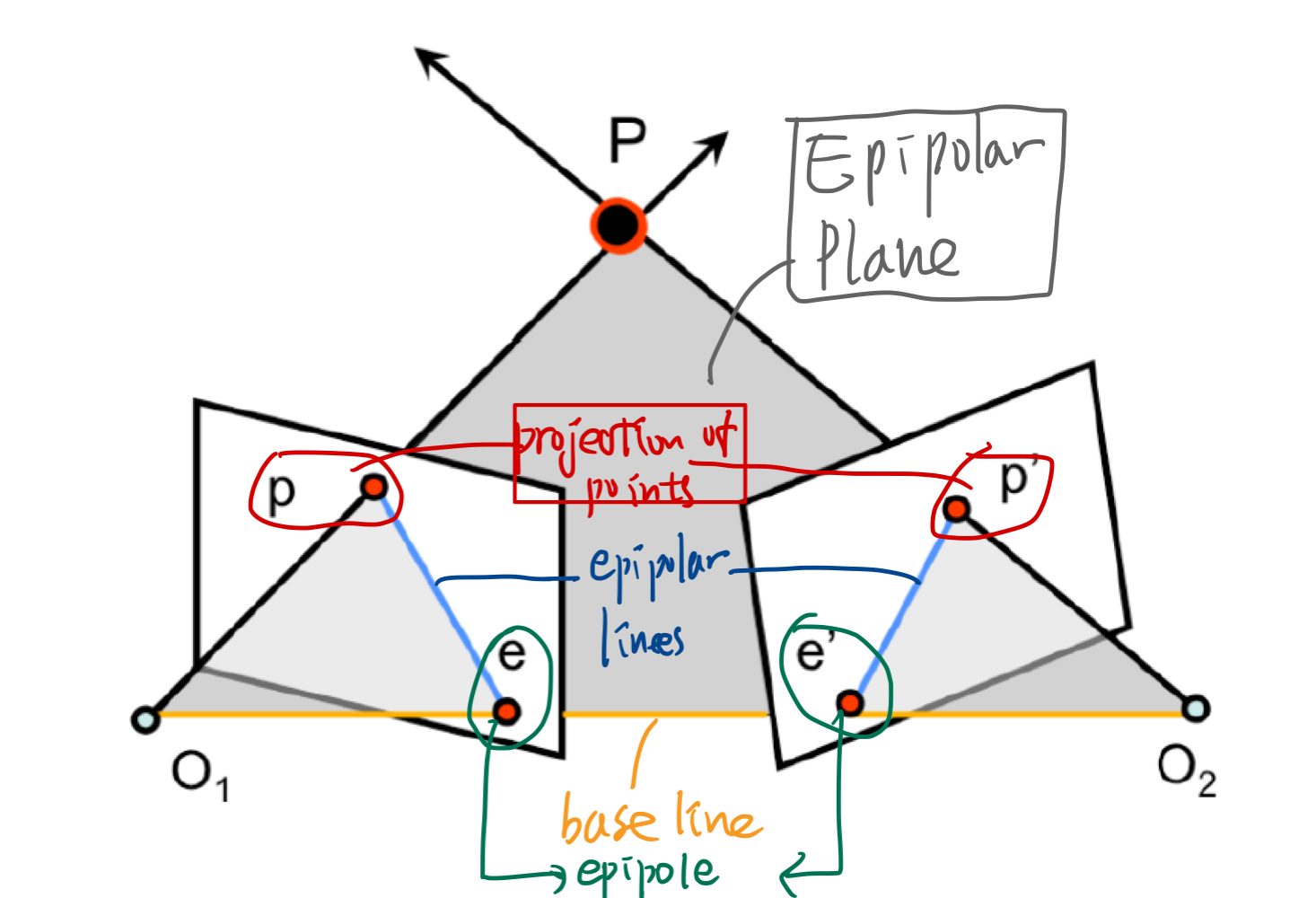
• Essential Matrix (E)의 정의
  • normalized image plane 에서의 매칭 쌍들 사이의 기하학적 관계를 설명
  • left view의 p와 행렬곱(matrix multiplication)으로 right view의 p'좌표로 변환시키는 matrix
  • 여기서 p와 p'(소문자임)은 normalized image plane에서의 u, v 좌표계를 의미
• Essential Matrix의 목적
  • 3차원 P위치를 모르거나 camera parameter가 주어지지 않는 상황에서
    • 한쪽 normalized image plane내의 한 점에 대응하는, 다른 view에서의 epipolar line을 찾을 수 있는 행렬
    • (normalized image plane 기준) 두 영상 좌표 p와 p'간 전환 관계를 나타내는 행렬
• 
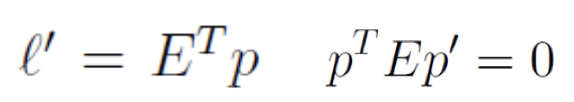
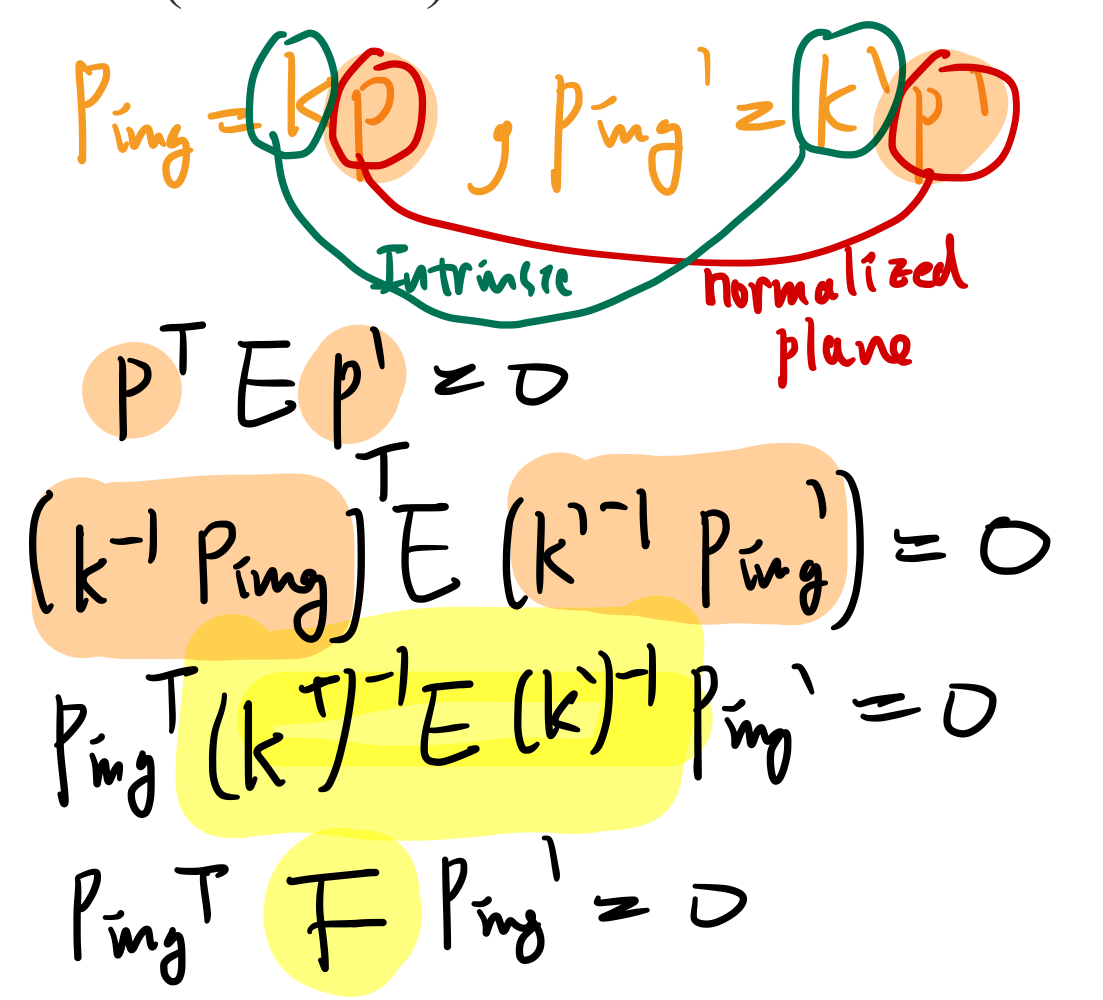
  • 위 식의 오른쪽을 essential (or epipolar) constraint라고 부른다.
  • TODO: (p')TEp = 0 으로 표현하기도 하던데, 둘 다 만족하는건지 확인 필요
• 위 식을 만족하는 E(Essential Matrix)가 [Tx]R 행렬이라는 것을 증명하기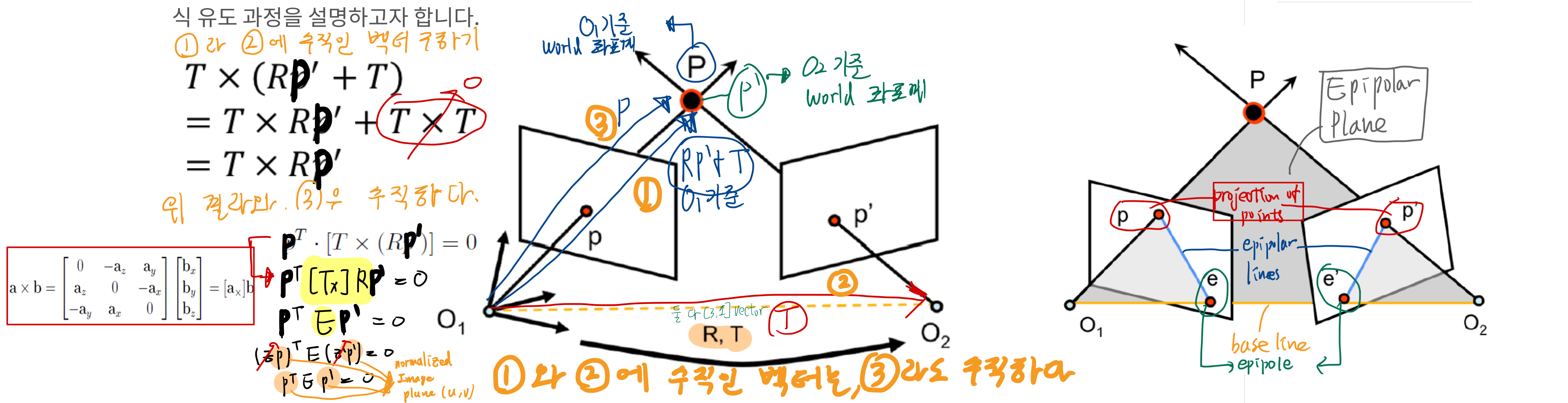
• 

3. Fundamental Matrix

• Fundamental Matrix의 목적
  • 카메라 intrinsic까지 포함한, 두 이미지 plane의 실제 pixel 좌표 사이의 기하학적 관계를 나타낸 행렬 (항상 이런행렬이 존재한다.)
  • Essential Matrix와 동일하게 다른 view에의 epipolar line을 찾을 때 사용
• 

4. Epipolar Geometry

4.1. epipolar constraint

• 
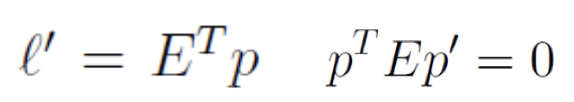
• 위 제약을 이용해서 뭘 구하고 싶은가? Fundamental Matrix!
  • 만약 내가, 각 카메라의 intrinsic을 알고 있다면,
    • Fundamental Matrix로부터 Essential Matrix를 얻을 수 있고,
    • Essential Matrix = [Tx]R 이므로,
      • 카메라 1 좌표계 기준, 카메라 2의 Extrinsic matrix를 구할 수 있습니다.

4.1.1. intrinsic을 모르는 경우

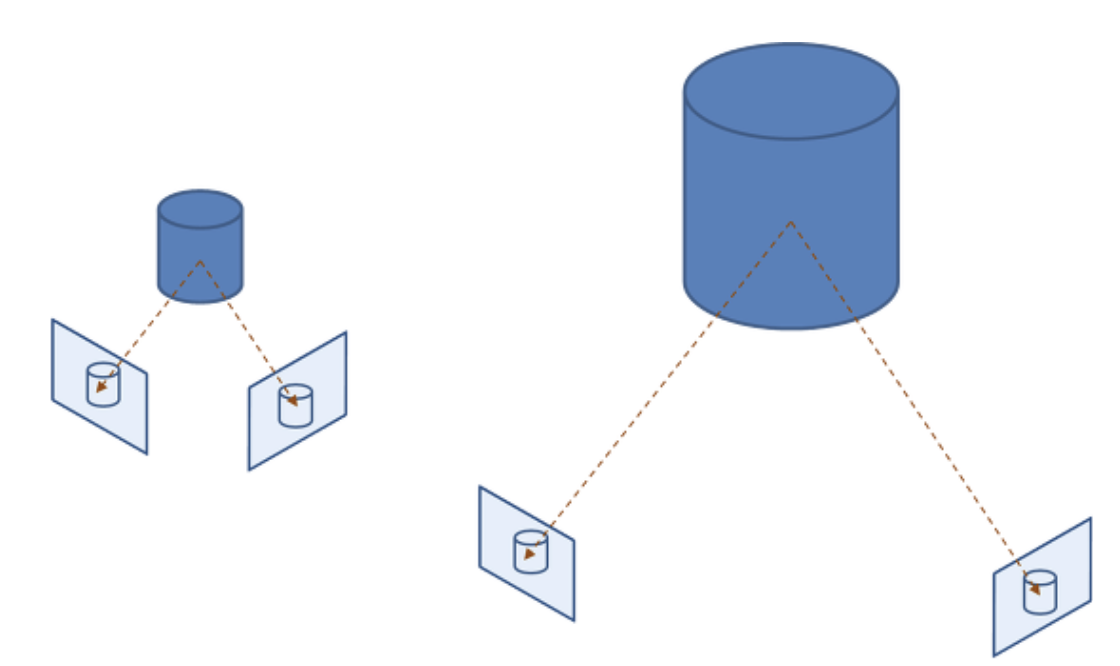
• 이미지 쌍의 7개의 매칭점을 알고 있으면, 우리는 epipolar constraint을 이용해서, Fundamental Matrix를 구할 수 있습니다.
• 단, 여기서 주의해야 할 점은 F의 스케일(scale)까지는 결정할 수 없다는 점입니다 (E도 마찬가지입니다).
• 가까이에 있는 작은 물체를 찍거나 멀리 있는 큰 물체를 찍어도 같은 영상을 얻을 수 있음을 상기하기 바랍니다.
• 

4.1.2. intrinsic을 아는 경우

• 만일 카메라 파라미터를 알고 있다면 Essential matrix E만 구하면 됩니다.
• Essential matrix E를 결정하기 위해서는 보통 5쌍의 매칭점을 필요로 합니다만
  • 알고리즘에 따라서는 8 쌍의 매칭점을 필요로 하는 경우도 있고, 어떤 경우에는 3쌍, 2쌍, 심지어는 1쌍의 매칭점만을 필요로 하는 경우도 있습니다.
• E는 R, t로 구성되는데 회전변환 R이 3 자유도, 스케일을 무시한 평행이동 t가 2 자유도, 도합 5 자유도이므로 5쌍의 매칭점을 필요로 함.
• Essential 행렬을 구할 때 몇 쌍의 매칭점들을 필요로 하느냐에 따라서 알고리즘을 8-point 알고리즘, 5-point 알고리즘, ..., 1-point 알고리즘 등과 같이 부릅니다.
  • 예를 들어, 3-point 알고리즘은 E를 구할 때 3쌍의 매칭점을 이용하는 알고리즘을 지칭합니다.
• 3-point 알고리즘, 2-point 알고리즘 등과 같이 원래 요구되는 매칭쌍(5쌍)보다 적은 수의 매칭쌍을 이용하여 E를 구할 수 있는 이유는
  • E에 추가적인 constraint를 가하기 때문입니다.
  • 예를 들어, 달리는 자동차에 장착된 카메라로 촬영한 영상들 사이에는,
    • 우리가 손으로 카메라를 들고 맘대로 찍은 영상과는 분명히 다른 어떤 추가적인 constraint가 존재합니다
    • (지면과의 높이가 고정된 점, 자동차의 pitch와 roll의 변화가 거의 없는 점 등).
    • 여기에 추가적으로 자동차의 모션을 원운동 또는 직선운동으로 모델링하게 되면 훨씬 적은 수의 매칭쌍만으로 E를 결정할 수 있게 됩니다.

4.2. triangulation

• triangulation (삼각측량법)은
  • 두 이미지 평면 사이의 기하학적 관계가 주어지고 (즉, E 또는 F가 주어지고),
  • 두 이미지 평면상의 매칭쌍 p, p'이 주어지면
    • 이로부터 원래의 3D 공간좌표 P를 결정할 수 있다는 것
• 바로 스테레오 비전에서 거리(depth)를 구할 때 하는 일입니다.