Vector & Matrix & Tensor
- 기계 학습에서는 입력된 샘플을 특징 벡터로 표현한다.
- 기계 학습에서는 Train set을 담은 행렬을 Design Matrix(설계행렬)이라고 한다.
Vector: 1차원 숫자 배열 표현Matrix: 2차원 숫자 배열 표현Tensor: 3차원 이상의 숫자 배열 표현- Scalar는 0차원 Tensor
- Vector는 1차원 Tensor
- Matrix는 2차원 Tensor
Norm & Similarity
Vector Norm
- 벡터의 크기를 정의할 때는 norm을 사용한다.
- p차 norm은 다음과 같이 정의한다.
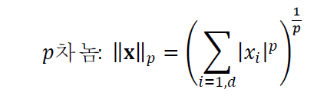
2-norm== Euclidean norm == L2 normInfinity-norm== 요소 값의 절대값 중 최대값

Matrix Norm
Matrix의 norm은 더 다양한 형태가 있는데,
기계학습이 주로 사용하는 Frobenius Norm만 살펴본다.
Frobenious Norm
- Frobenius norm : (요소들의 제곱의 합)의 제곱근
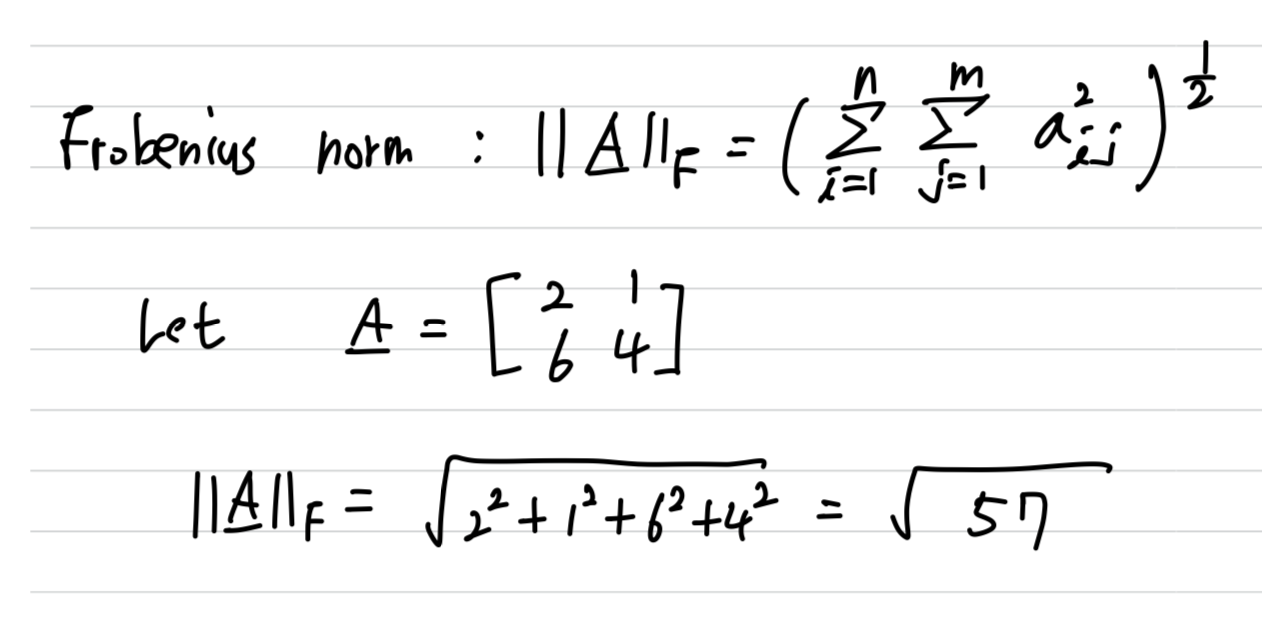
Similarity & Distance
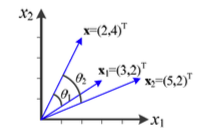
- 다음과 같이 기준이되는 vector가 존재하고
, vector가 존재할 때,둘 중 어떤 vector가 vector와 더욱 유사하다고 할 수 있는가?
== Similarity를 어떻게 측정할 것인가?
Similarity using Inner Product
내적은 두 벡터의 요소 간의 곱을 합산하여 Similarity 계산 ➡️ 하지만 문제 발생 가능
- 두 벡터가 똑같을 때() 가장 큰 값이 된다.
- 두 벡터가 수직일 때() 가장 작은 값이 된다.
- 벡터가 길기만 하면 Similarity가 커지는 문제가 있다.
- ex) = 14이고, 이므로 는 와 더 유사하다고 말해야 한다.
하지만 실제로는 는 와 더 유사하다.
- ex) = 14이고, 이므로 는 와 더 유사하다고 말해야 한다.
Similarity using Cosine Similarity
이를 해결하기 위한 대안으로
Cosine Similarity(코사인 유사도)가 있다.
- Cosine Similarity는 두 벡터 간의 각도를 사용하여 Similarity 계산.
따라서 내적과는 다르게 두 벡터의 크기에 의존하지 않게 된다.
➡️ 벡터의 크기가 중요하지 않은 문제에서 유용하게 사용된다- 단위 벡터로 변환한 다음, 단위 벡터의 내적을 사용하는 것이다.
- cosine_similarity는 다음과 같이 정의한다.
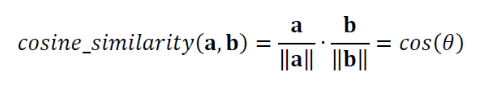
- 위의 2차원 벡터의 예시에서 Similarity 측정을 수행하였다.
하지만 똑같은 원리로모든 차원에 그대로 적용된다.

Similarity using Euclidean, Hamming, Manifold Distance, etc
-
Cosine Similarity는 특정 응용 분야에서는 적절하지 않을 수 있다.
예를 들어, 구매액과 방문횟수에 따라 고객을 분류하는 경우
단위 벡터로 만들면 크기 정보가 사라지므로 원래의 벡터를 사용해야 한다.
이 경우 Educlidean Distance를 사용해야 한다.- Euclidean Distance :
-
이진 벡터인 경우 서로 다른 값을 가진 요소의 개수로 정의하는
Hamming Distance, Manifold Distance 등이 있다.- Hamming Distance : 1, 2, 3 중에 골라 사용한다.
- / : 발생 가능한 최대 거리값
결국, 응용에 따라 적절한 방법을 선택해 사용하는 지혜가 필요.
퍼셉트론의 해석
classifier(decision line, plane, hyperplane)
Perceptron은 입력 샘플을 2개의 부류 중 하나로 분류하는 분류기(Classifier)이다.
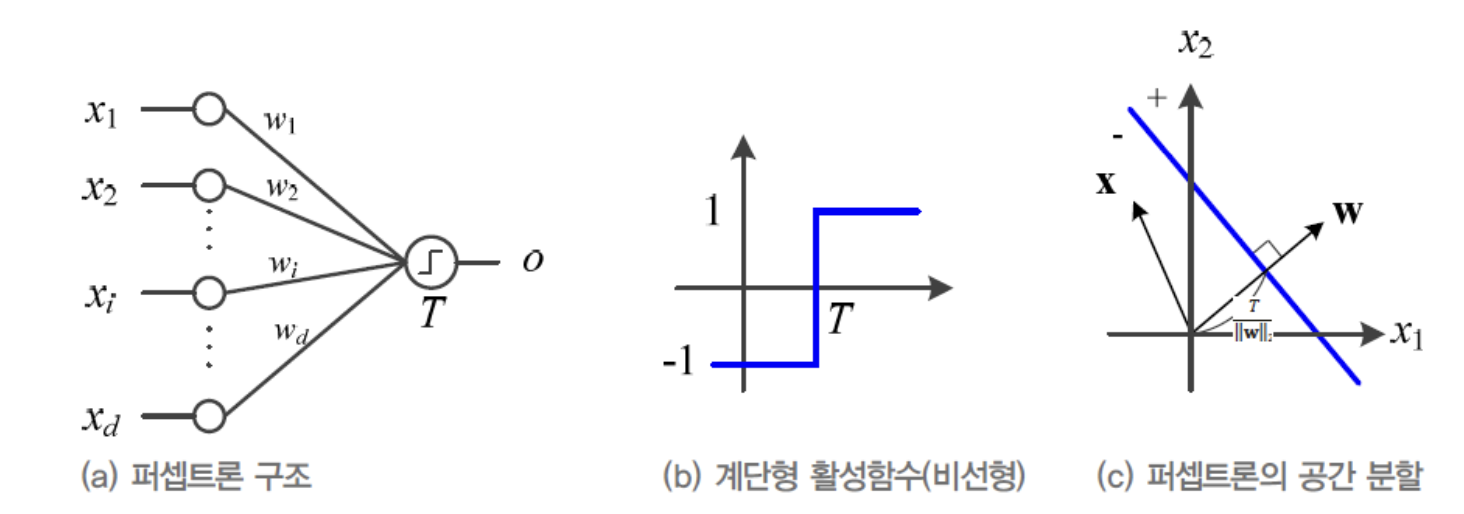
- (a)는 Perceptron의 구조이다.
- 입력 : 차원 특징 벡터
- 출력 :
- edge: 입력 노드와 출력 노드를 가중치()로 연결
-
퍼셉트론은 다음과 같이 동작한다.
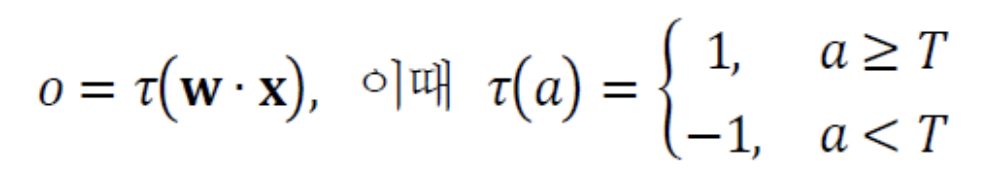
- == Activation Value(활성값) : 입력 값과 해당 edge의 가중치를 곱하여 더한 값.
- == Activation Function(활성함수)
- : 임계값 (임계값 이상이면 1, 아니면 -1)
- Activation Value()를 Activation Function()에 넣었을 때 출력되는 값이 가 된다.
-
(b) : 여기에서 Activation Function으로 계단함수를 사용했다.
-
(c) : decision line == 에 수직이고 원점으로부터 만큼 떨어져 있다.
- d=2, , 모두 2차원인 상황에서 파란선을
decision line(결정직선)이라고 한다. - d=3, 3차원이 되면
decision plane(결정평면)이라고 한다. - d>=4, 4차원 이상이 되면
decision hyperplane(결정초평면)이라고 한다.
- d=2, , 모두 2차원인 상황에서 파란선을
-
Example : 3차원 특징 벡터와 decision plane
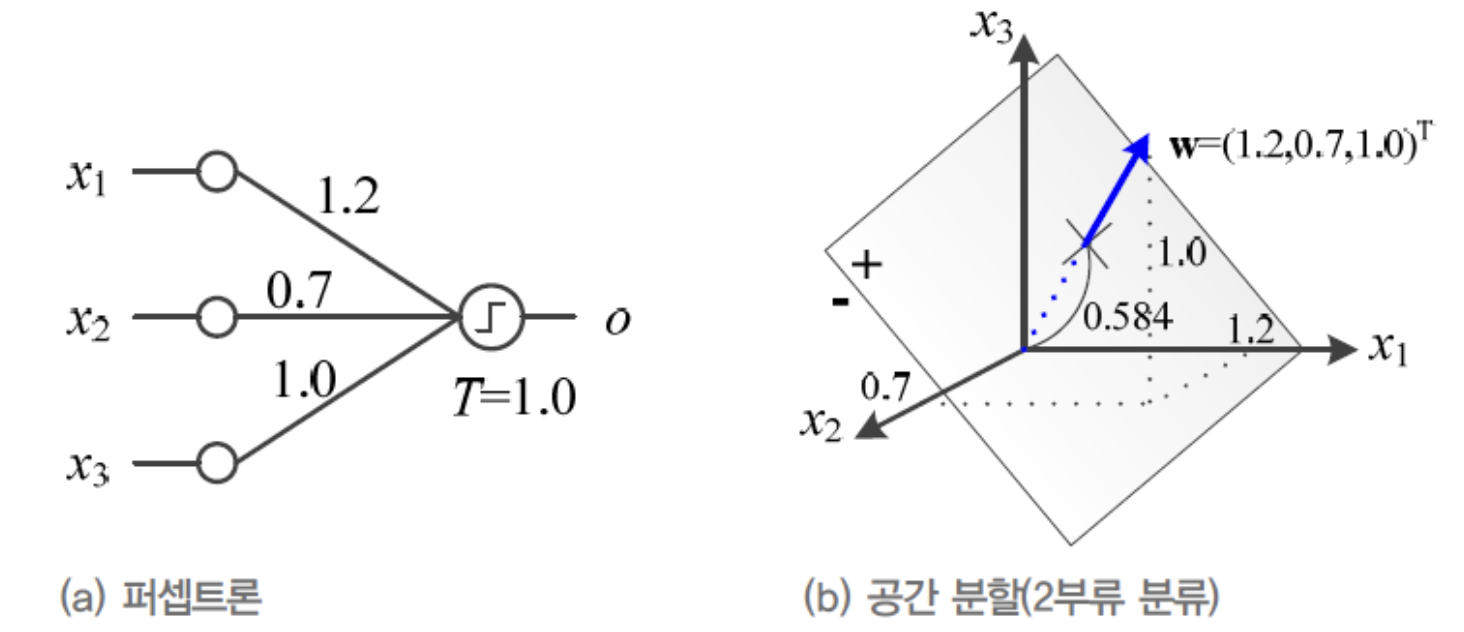

다중 퍼셉트론
- 여러 퍼셉트론을 묶어 다음과 같은 구조로 확장할 수 있다.
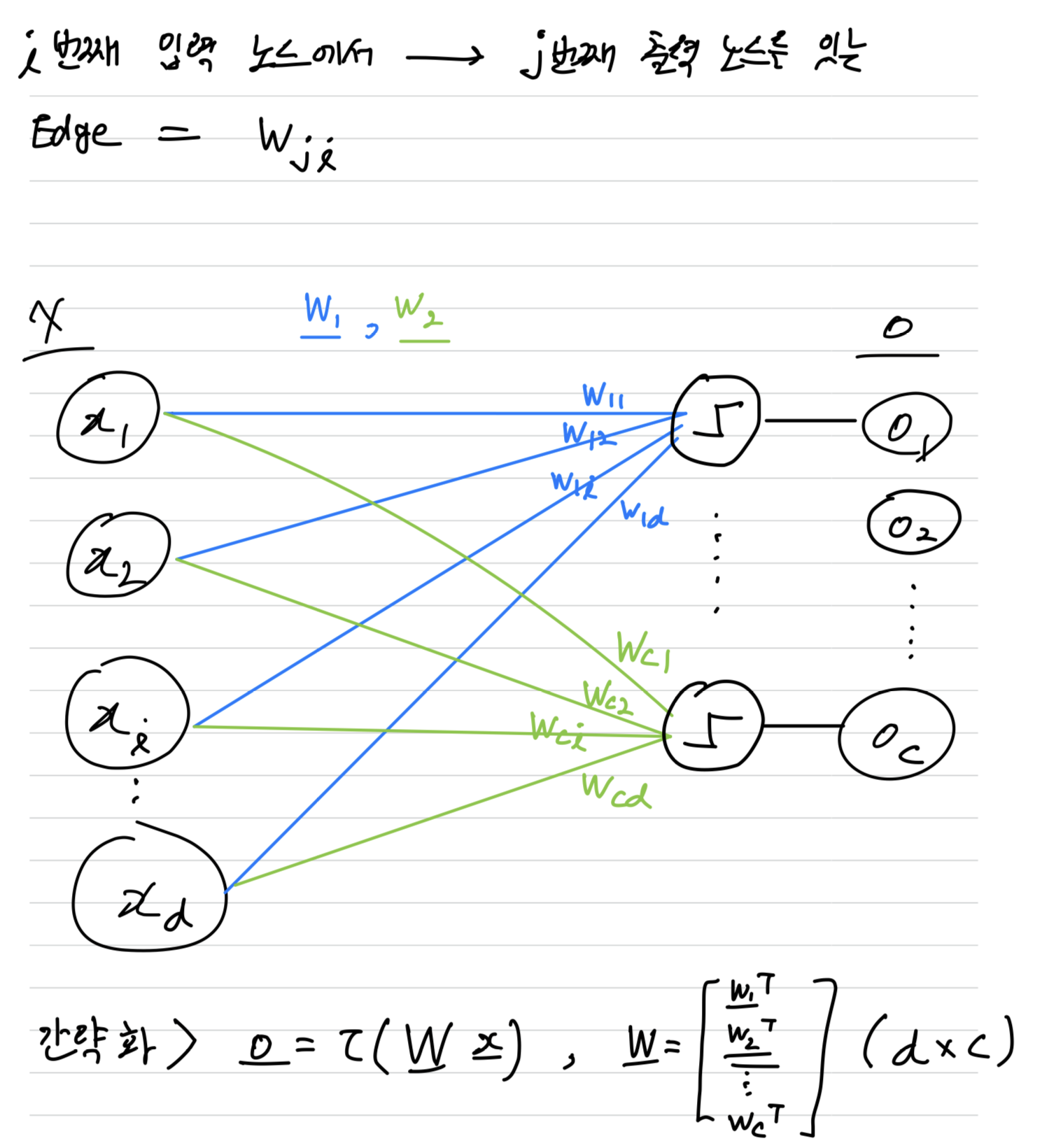
➡️ 가중치 벡터()를 각 부류의 기준 샘플이라고 생각하면,
신경망은 입력된 특징 벡터 에 대해 개의 부류와 유사도를 계산한다.
즉, 에 가까운 부류일수록 Activation Value가 크다.따라서 가장 큰 출력 노드를 최종 분류 결과로 취한다면,
이 신경망을 c 부류 Classifier로 사용할 수 있다.
학습의 정의
- 특징 벡터 와 부류 정보 의 쌍이 주어졌을 때,
모든 샘플을 제대로 부류하는 (가중치 행렬)를 구하는 문제가 바로 기계학습이다.
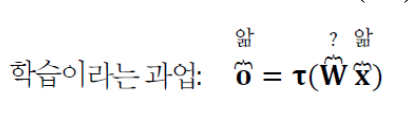
Linear Combination & Vector Space
basis vector란
basis vector(기저벡터)란
vector space(벡터 공간)의 모든 vector를 생성할 수 있는 일종의 기본 vector들이다.
i = (1, 0) : x축 방향으로 길이가 1인 벡터
j = (0, 1) : y축 방향으로 길이가 1인 벡터
- (2, 3)이라는 벡터는 2i + 3j로 나타낼 수 있다.
- (-1, 4)라는 벡터는 -1i + 4j로 나타낼 수 있다.
- 다음과 같이 각 vector의 길이가 1이고, 서로 수직인 basis vector를
orthonomal basis vector(정규직교 기저 벡터)라고 한다.
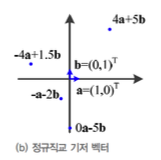
이렇게 기저벡터를 사용하면 어떤 벡터든 일정한 비율로 조합하여 표현할 수 있다.
Linear Combination
Linear Combination(선형 결합)은
basis vector들로 일정한 상수배와 덧셈을 통해 만들어지는 새로운 벡터를 말한다.
Vector Space
Vector Space(벡터 공간)은
Linear Combination을 통해 만들어진 공간을 말한다.
Linear Independence
Linear Independence(선형 독립)은
한 벡터를 다른 벡터의 선형 결합으로 표현될 수 없는 경우를 말한다.
-
선형 독립이 아닌 경우
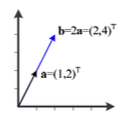
= : vector b는 vector a에 대한 스칼라 곱(선형 결합)으로 표현될 수 있다
➡️ 선형 독립이 아니다.
➡️ vector space는 직선에 불과하다. -
선형 독립인 경우
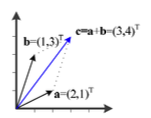
는 의 선형결합으로 표현될 수 없다.
➡️ 선형 독립이다.
➡️ vector space는 2차원 평면을 만든다.
Rank of Matrix
Rank of Matrix(행렬의 계수)는
행렬에서 1차 독립인 row vector의 개수이다.
즉, 유효한(유의미한) 방정식의 개수를 의미.
- rank(계수)를 알면 벡터 공간이 어떻게 생겼는지 알 수 있다.
- rank=1 ➡️ 1차원 vector space
- rank=2 ➡️ 2차원 vector space
- rank=3 ➡️ 3차원 vector space
- Matrix의 Rank가 vector의 차원과 같으면 Matrix가 Full Rank(최대 계수)를 가졌다고 한다.

Inverse Matrix
inverse matrix
: Matrix
-1 : Inverse Matrix
-1 = -1 =
어떤 행렬과 그것이 역행렬을 곱하면 Identity Matrix(단위행렬)이 된다.
singular matrix
역행렬이 없는 행렬을 singuluar matrix(특이행렬)이라고 한다.
nonsigular matrix
역행렬이 존재하는 행렬을 nonsingular matrix(정칙행렬)이라고 한다.
determinant
determinant(행렬식) 정사각행렬에 대해 정의되는 수학적인 개념으로,
행렬에 대한 선형변환의 성질을 나타내는 값이다.
- 계산 방법
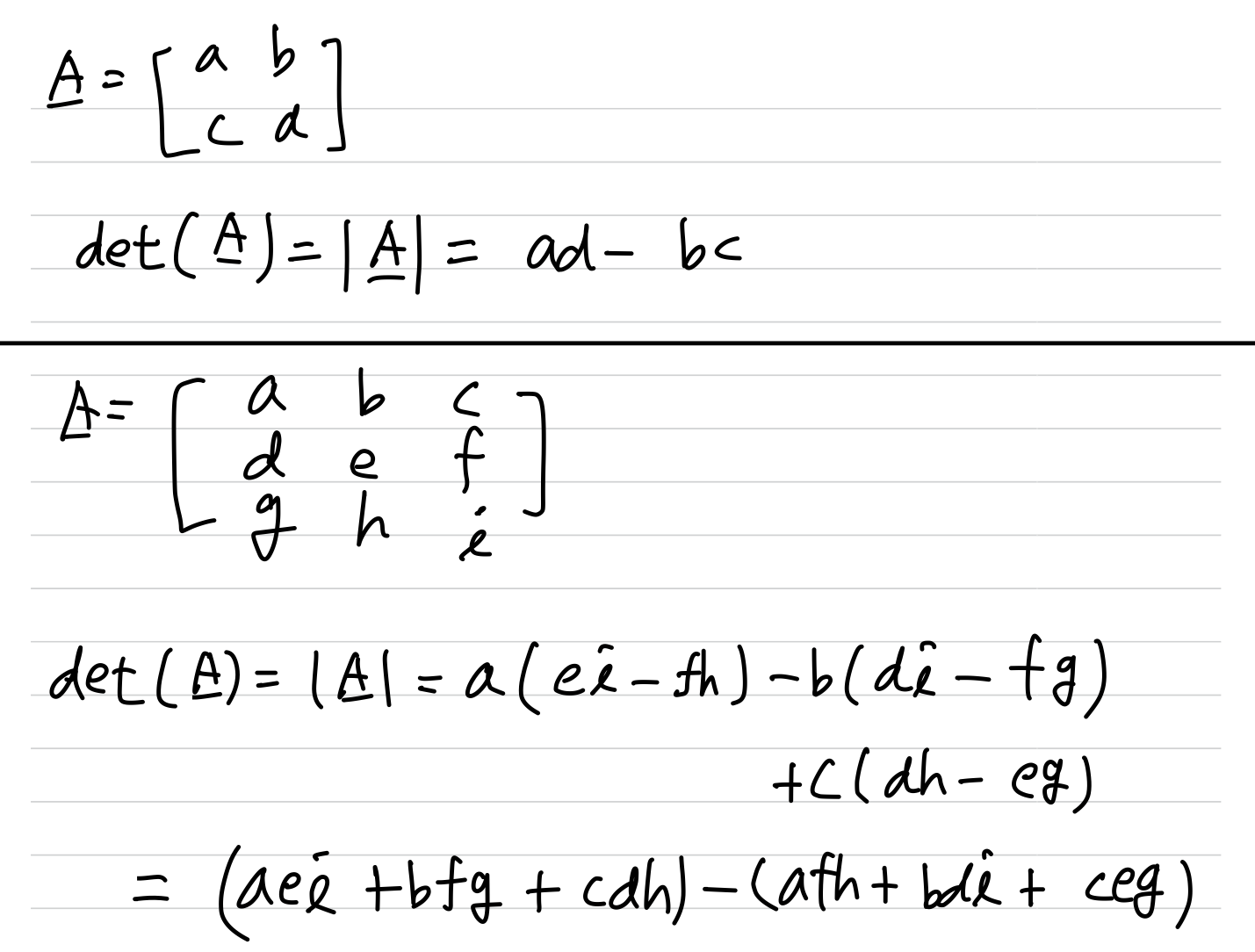
inverse matrix by determinant
- 다음과 같이 determinant를 이용하여 Inverse Matrix를 구할 수 있다.

필요충분조건 정리

Matrix Decomposition(Factorization)
행렬을 Decomposition(분해) 한다 == 인수 분해(Factorization)한다.
여기서는 eigen value(고윳값) 분해를 공부한다.
Eigen Value & Eigen Vector
- : Matrix
- : eigen vector
- : eigen value
- m * m Matrix는 최대 m개의 eigen value와 eigen vector를 가질 수 있다.
- 모든 eigen vector는 서로 orthogonal(직교)이다.
- 다음 예제에서 의 eigen value가 모두 0이 아니므로
- 는 역행렬을 가지며
- 는 positive definite symmetric matrix이다
Eigen Value & Eigen Vector, 기하학적 의미
- 반지름이 1인 원 위에 있는 4개의 벡터 , , , 가 에 의해 어떻게 변환되는지 살펴보자.
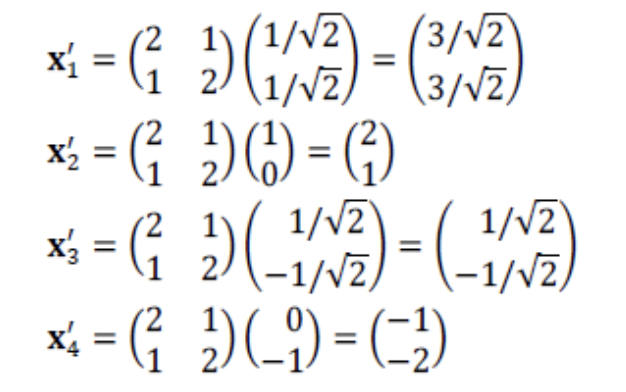
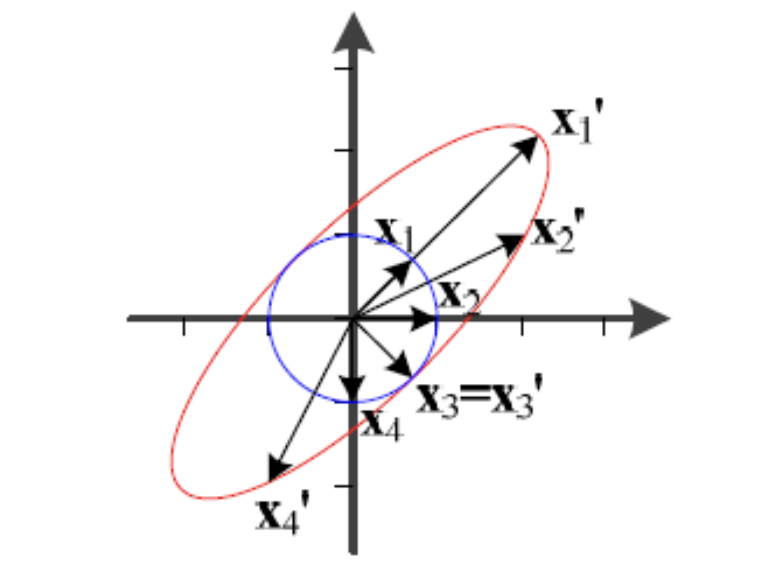
- 의 eigen vector와 , 는 방향이 같다.
두 vector는 변환에 의해 길이가 달라지더라도 방향은 그대로 유지된다.
이때, 길이 변화는 eigen value 를 따른다.
즉, 는 3배, 는 1배만큼 길이가 변한다.파란 원 위에 존재하는 수많은 점(벡터) 중에
방향이 바뀌지 않는 것은 고유 벡터에 해당하는 , 뿐이다.
- 의 eigen vector와 , 는 방향이 같다.
Normalization of an Eigen Vector
-
고유값은 정말로 고유하다.
고유 벡터를 고유하게 하기 위해서 정규화(단위 벡터화)한다.Normalization(정규화): 벡터의 크기를 조정하여 특정한 범위로 변환하는 것을 의미.
Unit Vectorization(단위 벡터화): 벡터의 크기를 1로 변환하는 것을 의미.
엄밀히 말하면 서로 다른 용어이지만,
여기서의 Normalization은 벡터의 크기를 1로 조정하는 Normalization(=단위 벡터화)이기 때문에 혼용.
-
Eigen Vector 정규화 방법 :

Positive Definite Matrix
Scalar에 부호를 부여하듯이 Matrix에도 부호를 부여할 수 있을까?
-
zero vector가 아닌 vector에 대해서,
다음과 같은 식을 만족하는 를 다음과 같이 정의할 수 있다.
: positive definite (양의 정부호 행렬)
: positive semi-definite (양의 준정부호 행렬)
: negative definite (음의 정부호 행렬)
: negative semi-definite (음의 준정부호 행렬) -
positive definite Matrix의 Eigen Value는 모두 양수이다.
EVD(Eigen Value Decomposition)
EVD는 Square Matrix에 대해서만 적용이 가능하다.
EVD(고유값 분해)는 행렬 를 다음과 같이 분해한다.
-1
- : Decomposition 대상 Matrix
- : 의 Eigen Vector를 Column에 배치한 Matrix
- : 의 Eigen Value를 Main Diagonal에 배치한 Diagonal Matrix(Ascending)
- example
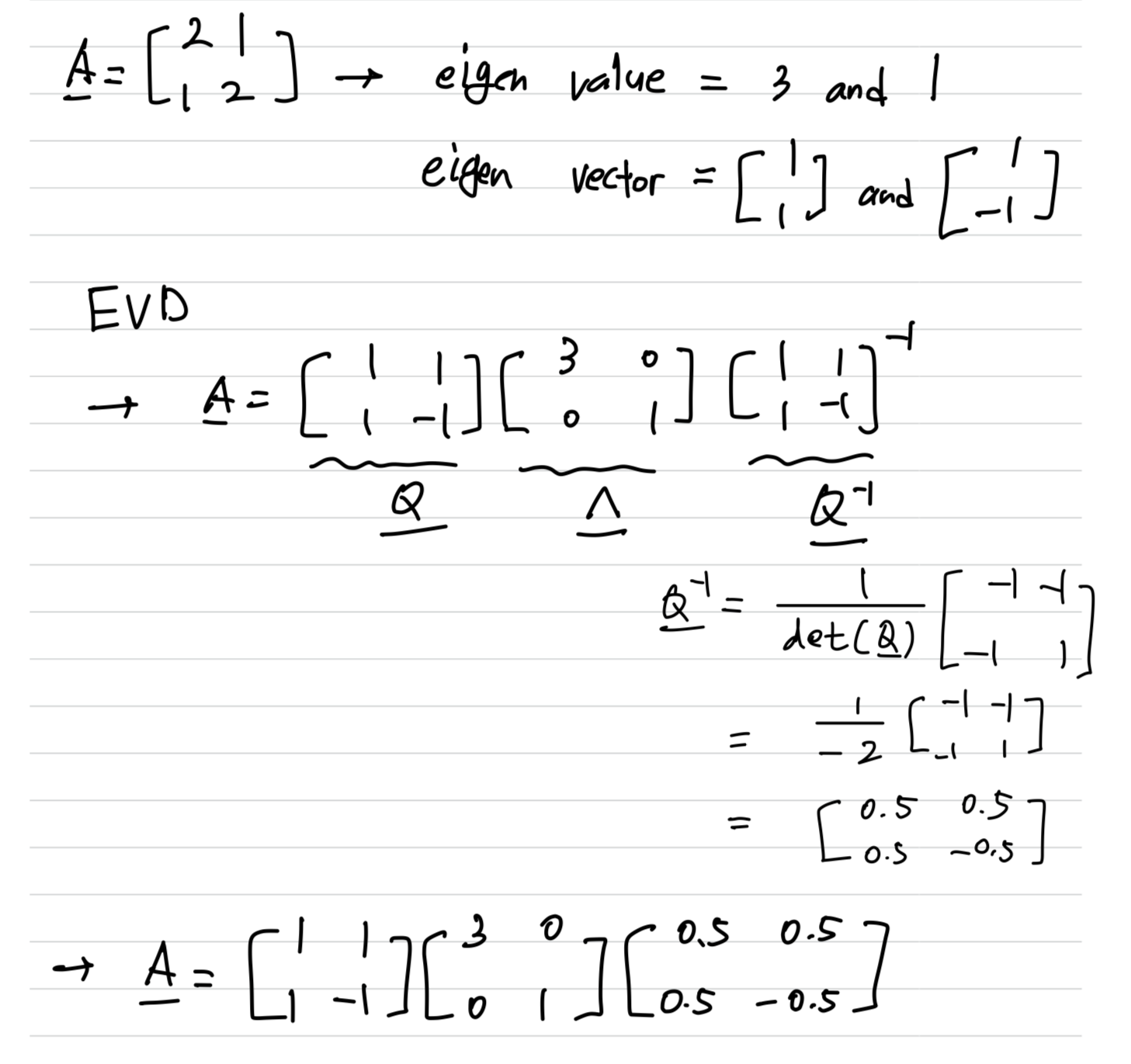
SVD(Singular Value Decomposition)
SVD는 Square Matrix뿐만 아니라 모든 Matrix에 대해서 적용이 가능하다.
SVD(특이값 분해)는 행렬 를 다음과 같이 분해한다
- : Decomposition 대상 Matrix
- = : 의 eigen vector을 column에 배치한 Matrix(n*n)
- 의 Column vector들을 left singular vector(왼쪽 특이 벡터)라고 함.
- : 의 Eigen Value의 제곱근을 Main Diagonal에 배치한 Diagonal Matrix(n*m)
- :의 eigen vector을 column에 배치한 Matrix(m*m)
- 의 Row vector들을 right singular vector(오른쪽 특이 벡터)라고 함.
