Search

탐색이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 의미한다.
대표적인 탐색 알고리즘으로 DFS, BFS를 꼽을 수 있다.
DFS, BFS를 이해하기 위해 스택, 큐, 재귀함수를 이해해야 한다.

Stack

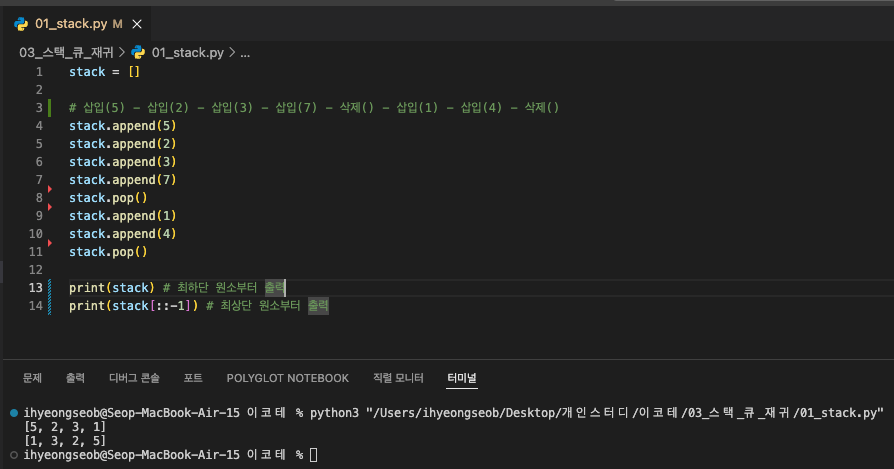
• Stack: 선입후출(First In Last Out), 후입선출(Last In First Out)
  • push : 삽입 → append() in Python
  • pop : 삭제
    

Queue

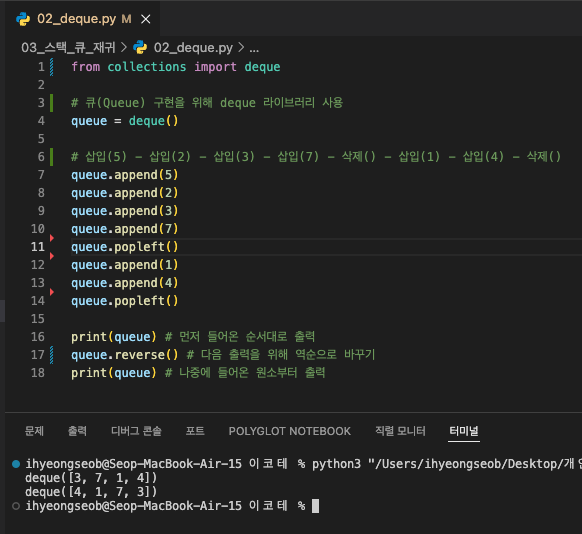
• Queue: 선입선출(First In First Out), 후입후출(Last In Last Out)
  • enqueue : 삽입 → append() in Python
  • dequeue : 삭제 → popleft() in Python
    

Recursive Function

• 자기 자신을 다시 호출하는 함수

• 재귀 함수의 장점 :
  재귀 함수는 수학의 점화식(재귀식)을 그대로 소스코드로 옮겼기 때문에 간결하다.
  수학에서 점화식은 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것을 의미한다.

• 재귀 함수의 단점 :
  컴퓨터에서 함수를 연속적으로 호출하면 메모리 내부의 스택에 쌓이게 된다.
  재귀함수를 너무 많이 호출하면 프로그램이 할당받은 메모리가 부족하게 된다.
  $\to$ 그래서 스택을 사용해야 할 때 구현상 스택 라이브러리 대신 재귀 함수를 이용할 수 있다.

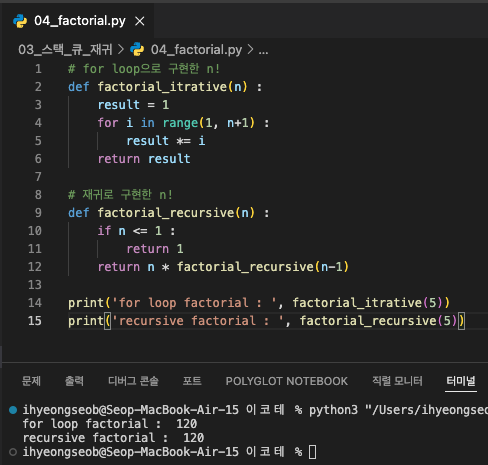
• ex. 팩토리얼을 수학적 점화식으로 표현해보면 ?

  1. n이 0 혹은 1일 때 : $factorial(n) = 1$
  2. n이 1보다 클 때 : $factorial(n) = n*factorial(n-1)$

Example 1

• 💡 예제 1 : 100번째 출력했을 때 종료되도록 종료 조건 명시

def recursive_function(i) :
    if i == 100 :
        return
    print(i, '번째 재귀 함수에서', i+1, '번째 재귀 함수를 호출합니다')
    recursive_function(i+1)
    print(i, '번째 재귀함수를 종료합니다.')

recursive_function(1)

Example 2: Factorial

Example 3: GCD

💡 예제 3 : 최대공약수 계산
두 개의 자연수에 대한 최대공약수를 구하는 대표적인 알고리즘으로는 유클리드 호제법이 있다.

유클리드 호제법 ➡️

• 두 자연수 A, B에 대하여 (A<B) A를 B로 나눈 나머지를 R이라고 하자.
• 이때 A와 B의 최대 공약수는 B와 R의 최대공약수와 같다.

ex. GCD(192, 162)
192 % 162 = 30 -> GCD(192, 162) == GCD(162, 30)
162 % 30 = 12 -> GCD(162, 30) == GCD( 30, 12)
30 % 12 = 6 -> GCD( 30, 12) == GCD( 12, 6)
12 % 6 = 0 -> GCD( 12, 6)

#include <iostream>

using namespace std;

int GCD(int _a, int _b) {
   if (_a % _b == 0){
       return _b;
   }
   else {
       return GCD(_b, _a % _b);
   }
}

int main(void){

   int a = 192, b = 162;

   cout << GCD(a,b) << endl;

   return 0;
}