Graph 표현

• Graph를 표현하는 2가지 방법 :
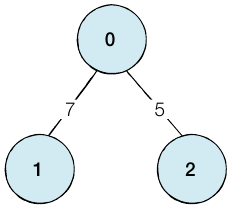
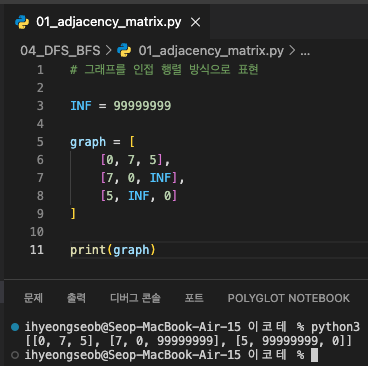
  1. adjacency matrix : 2차원 배열로 그래프 연결 관계 표현
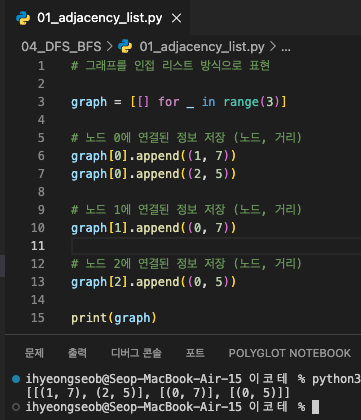
  2. adjacency list: list로 그래프 연결 관계 표현

메모리 측면
메모리 측면에서 보면 인접 행렬 방식은 노드 간 모든 관계를 저장하므로 노드 개수가 많을 수록 메모리가 불필요하게 낭비된다.
반면에 인접 리스트 방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다.

속도 측면
위와 같은 속성 때문에 인접 리스트 방식은 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.

	메모리	연결정보 얻는 속도
인접 행렬	비효율	빠름
인접 리스트	효율	느림

---

Adjacency Matrix (인접 행렬)

2차원 배열로 그래프의 연결 관계를 표현하는 방식

Adjacency List (인접 리스트)

리스트로 그래프의 연결 관계를 표현하는 방식

---

DFS (Depth-First Search)

• DFS(Depth-First Search)는 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
  DFS는 Stack 자료구조(또는 recursive function)를 이용한다.

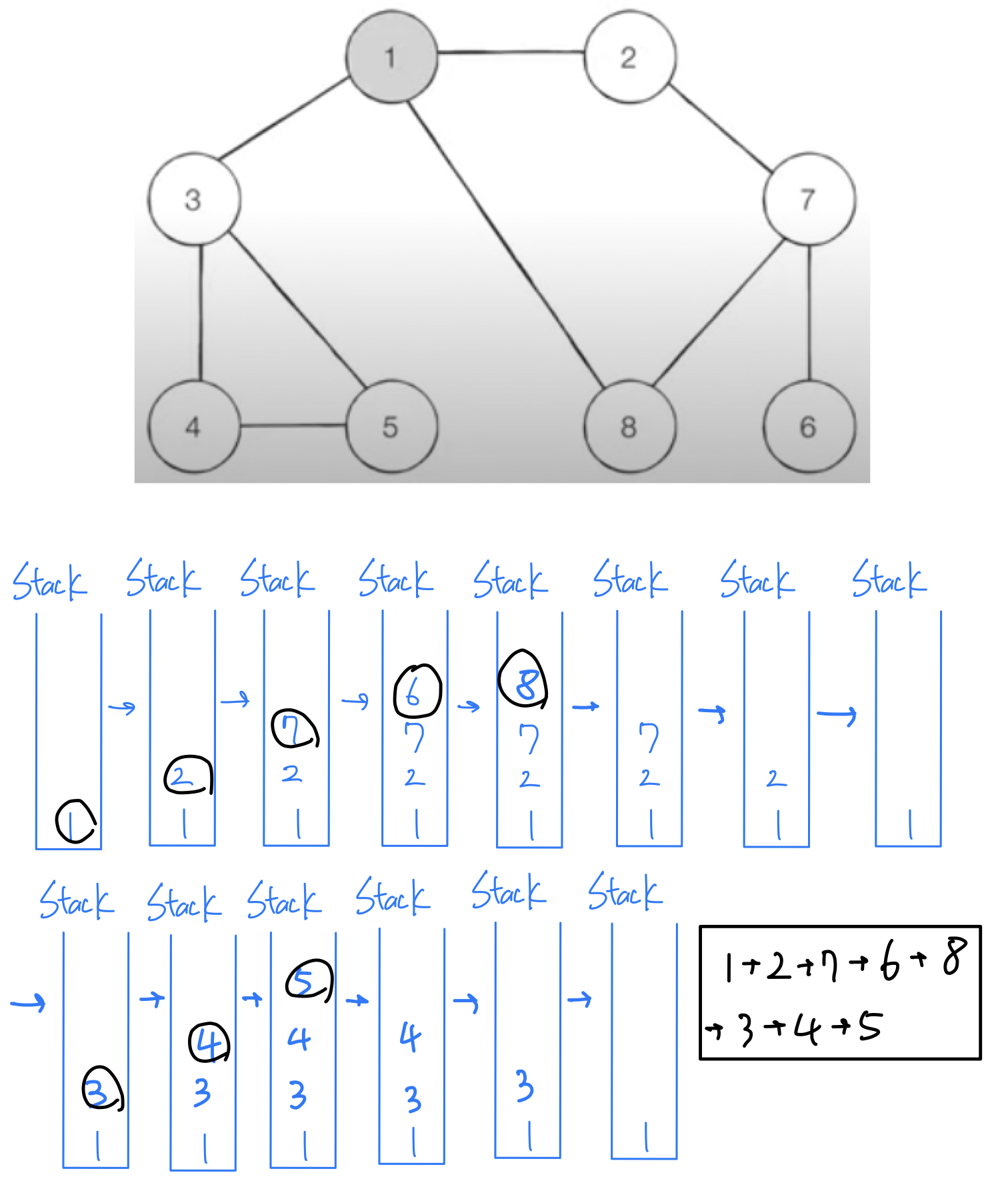
• 구현 방법

  1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
  2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문처리를 한다.
     방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
  3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
     
     

Example

---

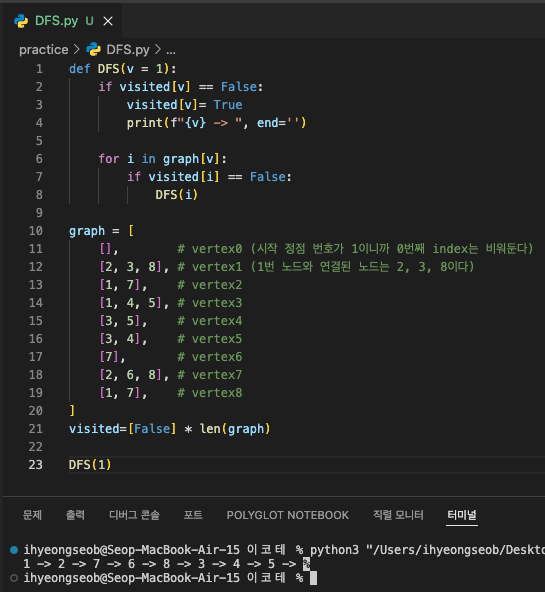
BFS (Breadth-First Search)

• BFS(Breadth-First Search)는 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
  BFS는 Queue 자료구조를 이용한다.

• 구현 방법

  1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
  2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
  3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.

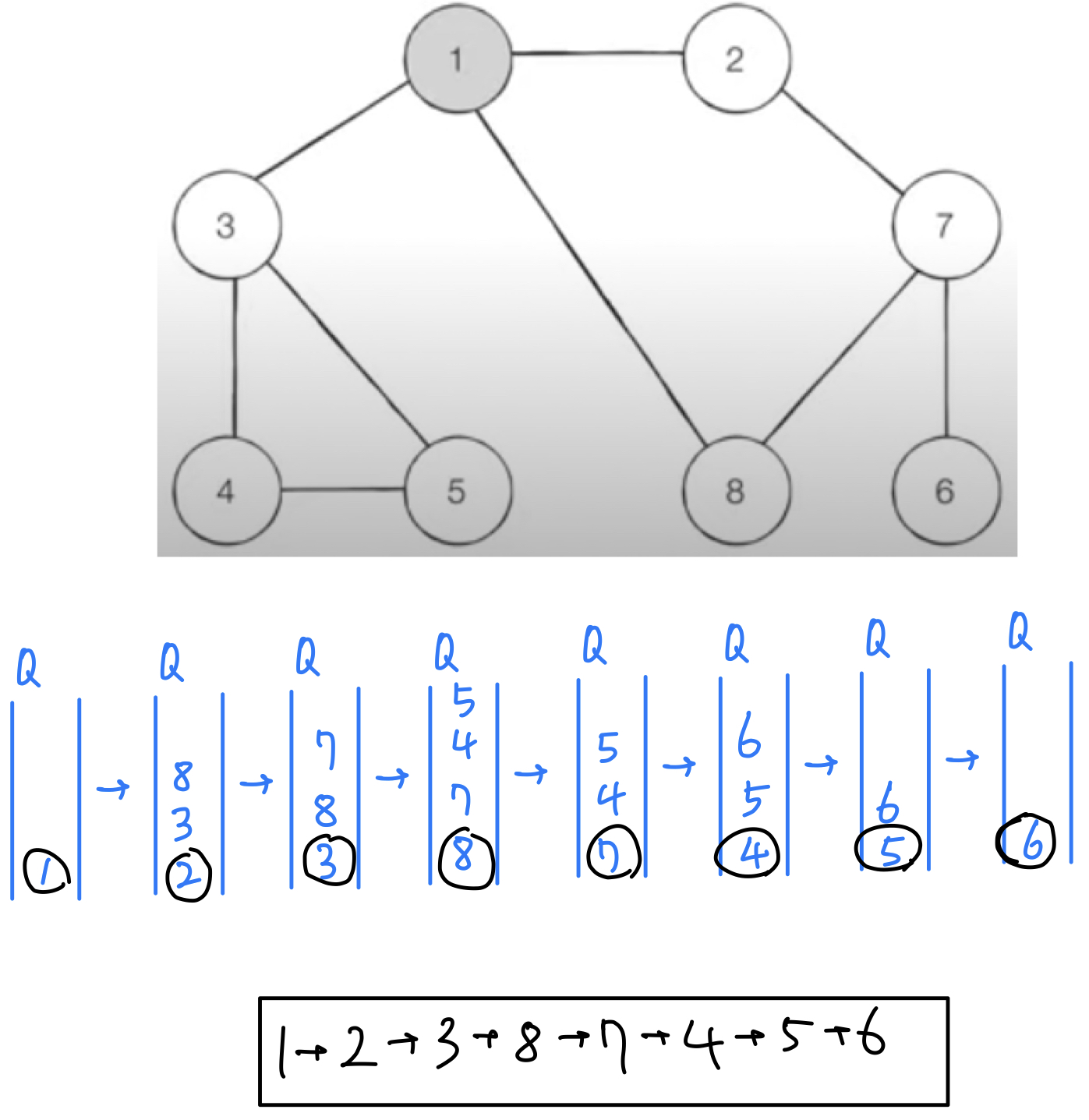
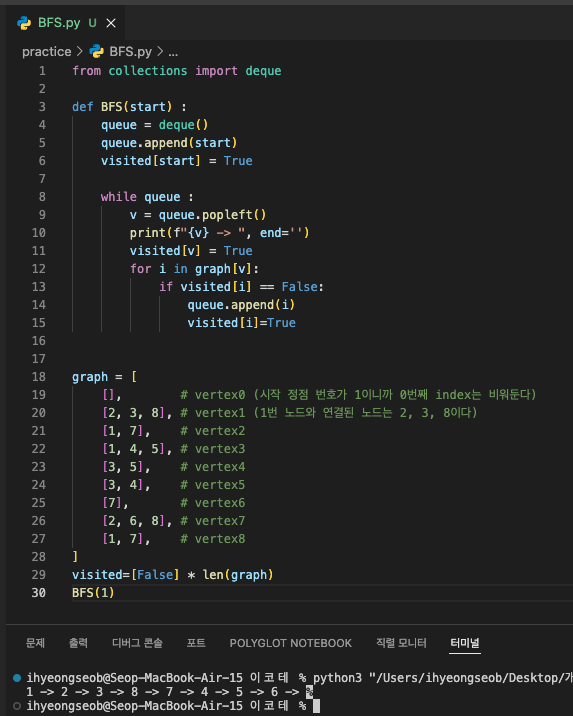
Example

• 예시
  

음료수 얼려먹기

문제 설명 :

문제 풀이 :

나의 아이디어 :

1. 그래프에서 0인 부분을 찾는다
2. 찾았으면, 인접 노드 중 값이 0인 노드만 방문하여 갈 수 있는 데 까지 탐색(DFS or BFS)하며 방문 처리를 한다.
3. 2 과정을 수행했으면 cnt값을 1증가
4. 그래프에서 0인 부분이 사라질 때까지 1과정 진행

#include <iostream>
#include <vector>

using namespace std;

void showGraph(vector<vector<int>> _graph) {
    cout << endl;
    for (auto& i : _graph)
    {
        for(auto j : i){
            cout << j << " ";
        }
        cout << endl;
    }
    
}

void DFS(vector<vector<int>>& _graph, int _i, int _j){

    // graph가 아닌 곳을 탐색하면 return
    // i(행)을 가리키는 index가 0 미만이거나 n 이상이면 graph 밖을 참조 (_graph.size() --> n)
    // j(열)을 가리키는 index가 0 미만이거나 m 이상이면 잘못된 곳 참조   (_graph[0].size() --> m)
    if(_i < 0 || _i >= _graph.size() || _j <0 || _j >= _graph[0].size()){
        return;
    } 
    
    // 지금 이곳이 0(뚫린 부분)라면 방문 처리
    if(_graph[_i][_j] == 0){
        _graph[_i][_j] = 2;
    }
    else {
        return;
    }

    // 상 방향 탐색
    DFS(_graph, _i - 1, _j);

    // 하 방향 탐색
    DFS(_graph, _i + 1, _j);

    // 좌 방향 탐색
    DFS(_graph, _i , _j - 1);

    // 우 방향 탐색
    DFS(_graph, _i, _j + 1);

}

int main(void){

    int n,m;
    int cnt = 0;
    cin >> n >> m;
    getchar();

    vector<vector<int>> graph;

    // graph를 입력 받는다
    for (int i = 0; i < n; i++)
    {
        vector <int> temp;
        string user_input;
        getline(cin, user_input);
        for (int j = 0; j < m; j++)
        {
            temp.push_back(user_input[j] - '0');
        }
        graph.push_back(temp);
    }
    
    // graph 에서 0인 곳을 찾는다
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            // graph에서 0인 부분이 있는데 아지 방문하지 않았다면 그곳에 가서 주변을 DFS
            if(graph[i][j] == 0) { 
                cnt++;
                // 해당 vertex에서 DFS를 진행하여 서로 연결되어 있는 부분 graph를 모두 방문 처리
                DFS(graph, i, j);
                showGraph(graph);
            }
        }
    }
    
    cout << cnt << endl;

    return 0;
}

---

미로 탈출

문제 설명 :

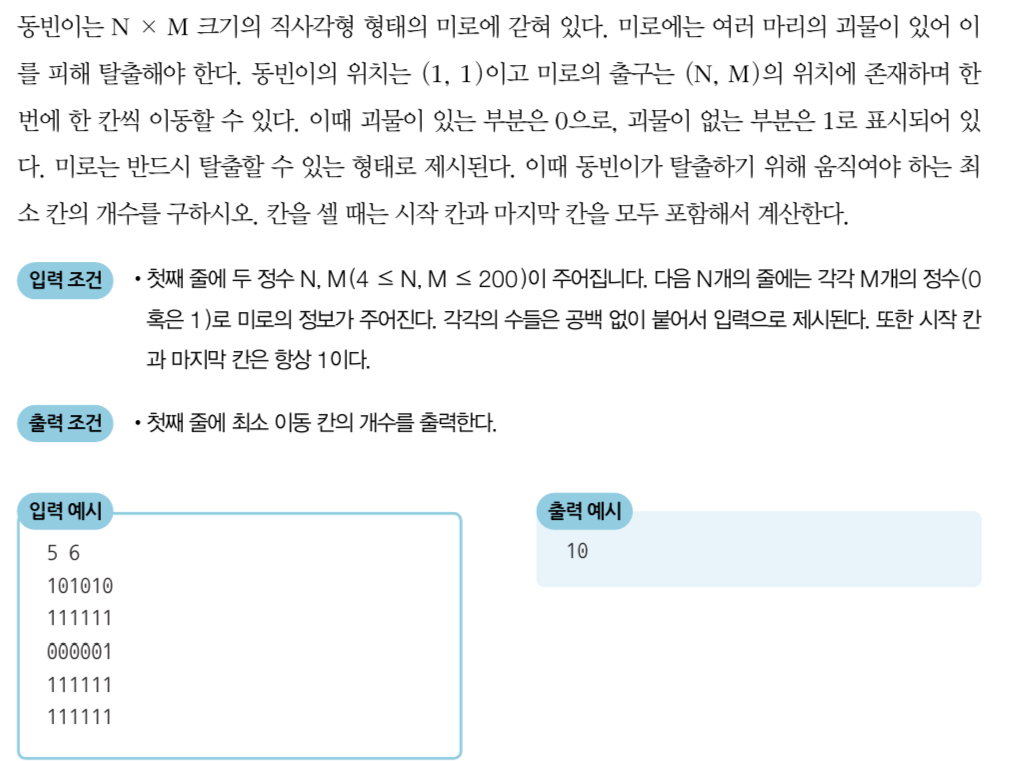
아이디어 :

1. BFS(넓이 우선 탐색)을 실행하여 인접노드까지 탐색하며 거리를 갱신한다.
   (BFS를 실행할 때마다 최단경로가 1씩 증가하는 것이다.)
2. 목표지점인 (n,m)에 도달하면 BFS를 실행한 횟수가 곧 최단경로가 된다.
   (n,m)에 도달할 때까지 1과정을 수행한다.

문제 풀이 :

from collections import deque

n, m = map(int, input().split())

graph = []
for i in range(n) :
   graph.append(list(map(int, input())))

# 동서남북
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]

def showGraph() :
   for i in range(n) :
       for j in range(m) :
           print(graph[i][j],end=' ')
       print('\n')
   print('\n')

def BFS(x, y) :
   queue = deque()
   queue.append((x, y))

   while queue :
       x, y = queue.popleft()

       for i in range(4) :
           nx = x + dx[i]
           ny = y + dy[i]
           if nx < 0 or nx >= n or ny < 0 or ny >= m :
               continue
           if graph[nx][ny] == 0 :
               continue
           if graph[nx][ny] == 1 :
               graph[nx][ny] = graph[x][y] + 1
               queue.append((nx, ny))
       
       showGraph()
   
   return graph[n-1][m-1]

print(BFS(0,0))