Training Multilayer Perceptron

Two types of signals in neural networks

1. Function Signals == Feed Forward
   • Propagates forward
2. Error Signals == Backward Propagation
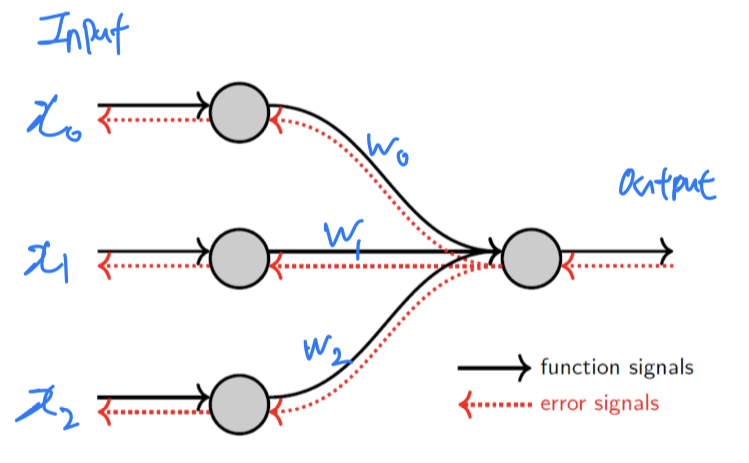
   • Propagates backward
     

Training by forward/backward propagation

• Forward Propagation
  

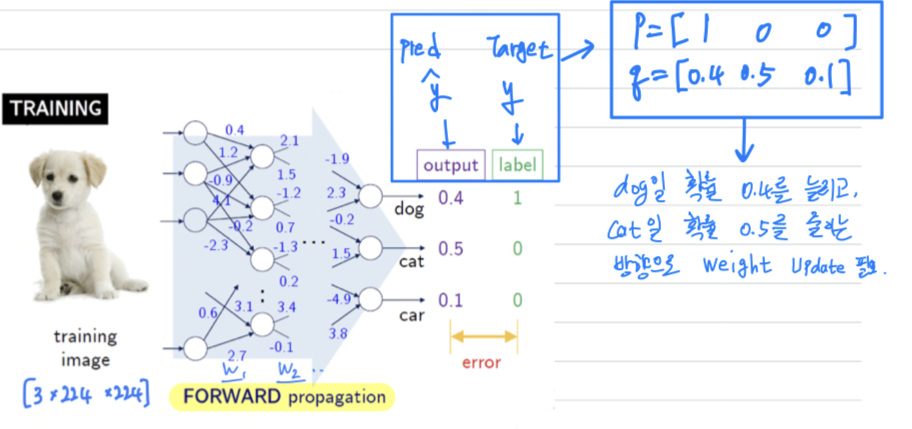
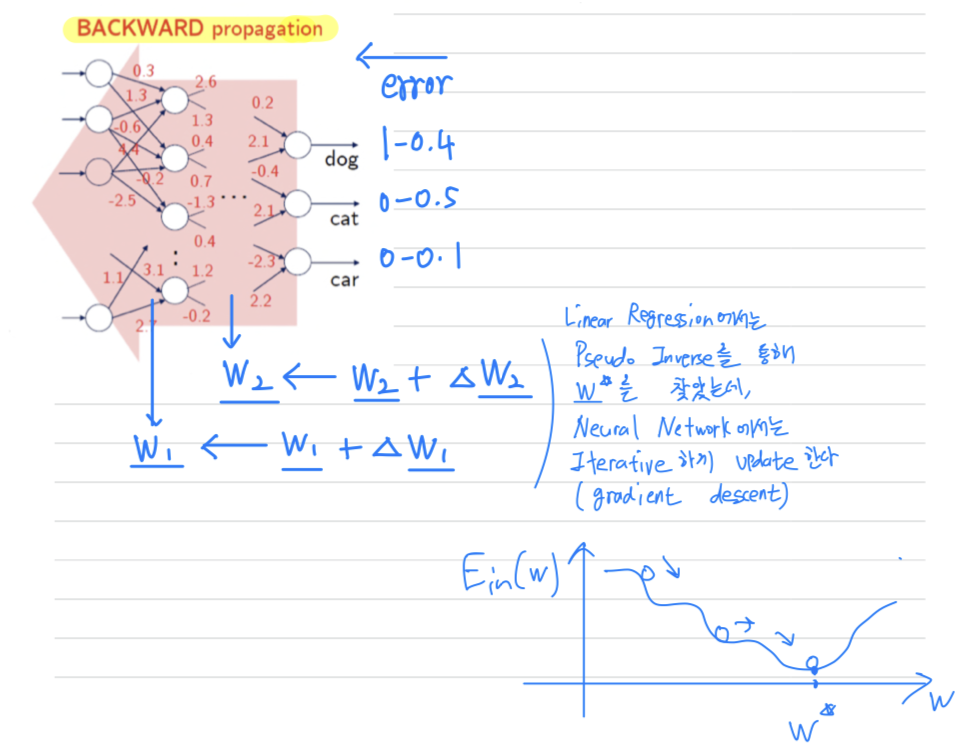
• Backward Propagation
  

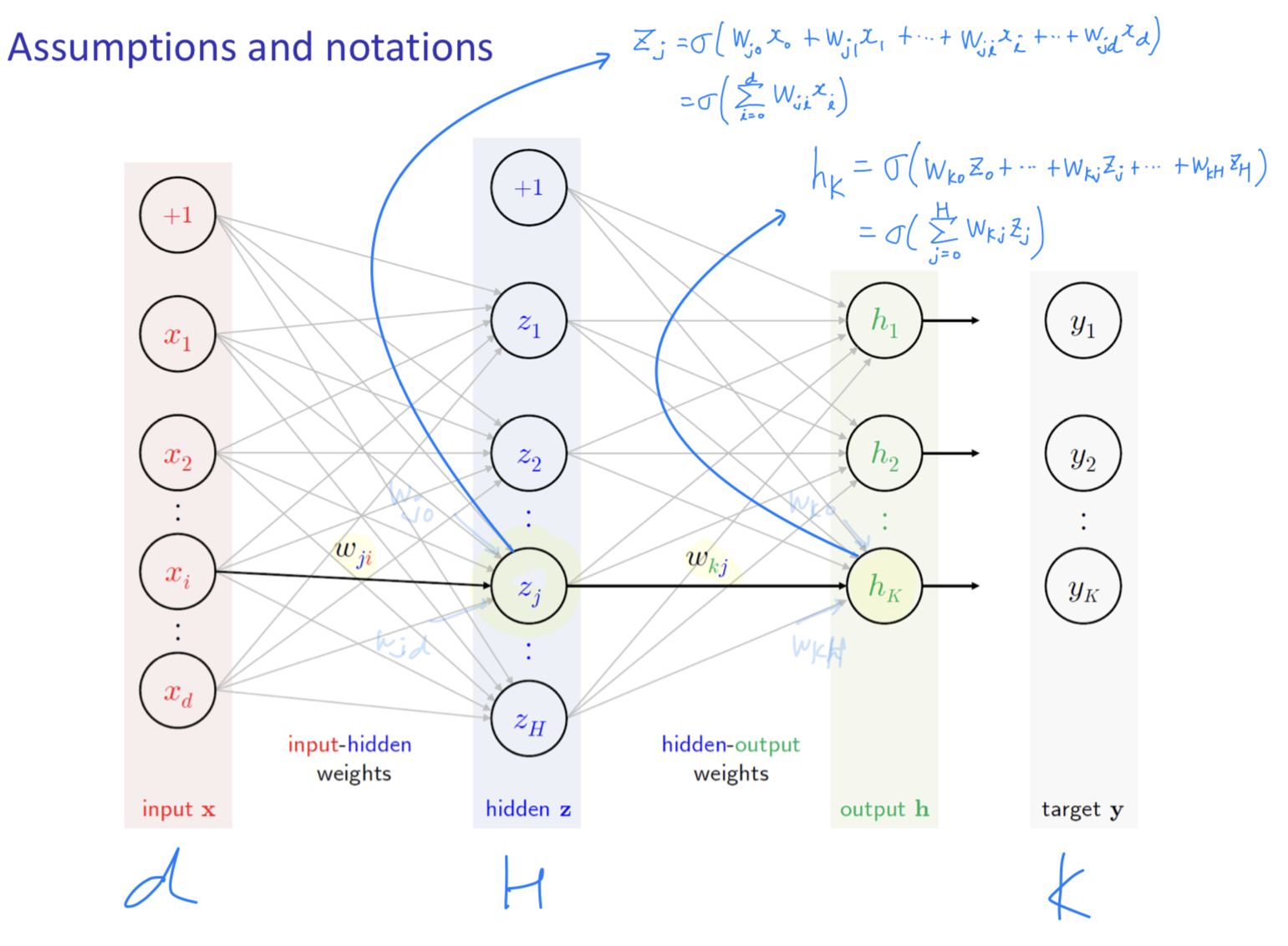
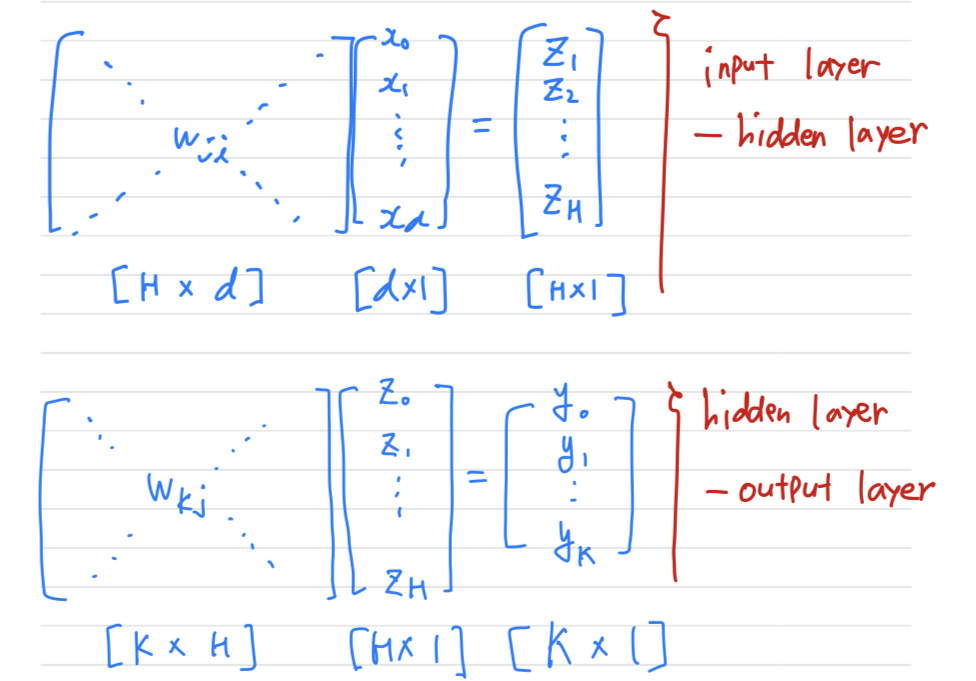
Assume & Notation (d-H-K)

• $d$ : dimensional input (input layer neuron 수)
• $H$ : H units in hidden layer (hidden layer neuron 수)
• $K$ : output signal (output layer neuron 수 == the number of Classes)
  

Error Measure

• $e_k$ : error signal on $k-th$ output (K번째 Class마다의 error값)
• $\epsilon_n$ : error energy on example $(x_n, y_n)$(n번째 data에 대한 전체 Class의 error)➡️ Sum of Squared Errors
• $\epsilon_D$ : mean-squared error on data $D$ (전체 data set에 대한 error)

Learning Objective

• Find $w$ that minimizes training error $\epsilon_D$
  that $w$ is $w^*$ ➡️ optimal weight
  

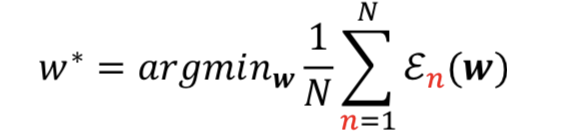
Selecting optimization method for neural networks

• First-order online methods (stochastic gradient descent) are commonly used
• Iterative optimization
  • Weight(Parameter) Update는 Error에 의존한다 : $\frac{\partial \epsilon}{\partial w}$
  • $w$ ⬅️ $w - \eta \Delta \epsilon(w)$

Credit assignment problem

• Credit assignment problem :
  

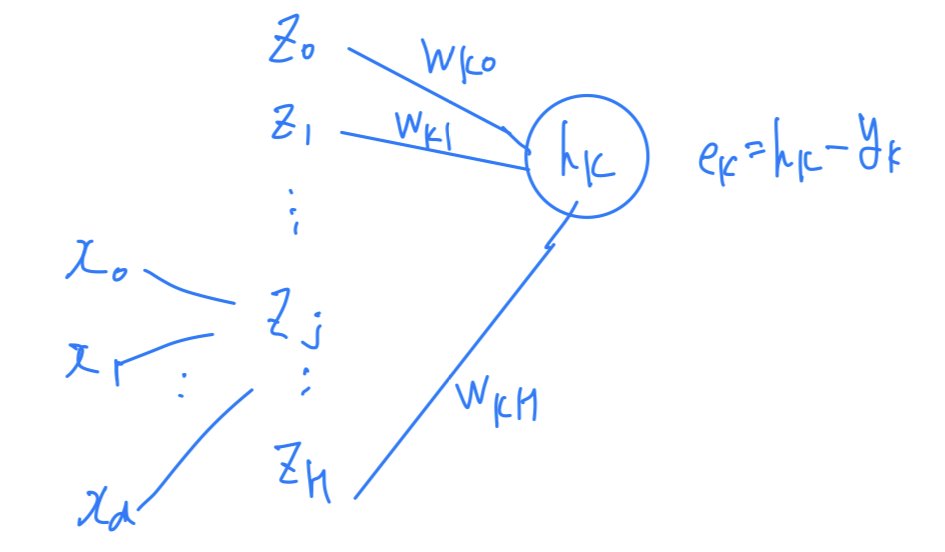
  • $e_k$가 계산되기 위해서는 $H$개의 hidden node로부터 영향을 받았기 때문에
    $e_k$에 대한 error 지분을 $z_0$~$z_H$에게 할당하는 문제
    ➡️ Hidden-to-output Layer에 대해서
    $h_k$와 $e_k$라는 것이 명확하게 정해지니까
    Credit assignment problem이 수월하다.

    • Sensitivity : $\frac{\partial \epsilon}{\partial w_{kj}}$

    ➡️ Input-to-hidden Layer에 대해서
    $z_j$라는 signal이 명확하게 알지 못하기 때문에
    Credit assignment problem이 어렵다.

• Hidden-to-output Layer에 대해서 Credit assignment problem이 수월했지만,
  Input-to-hidden Layer에 대해서는 그렇지 않았다.
  ➡️ 이를 극복하기 위해 back propagation을 사용한다.

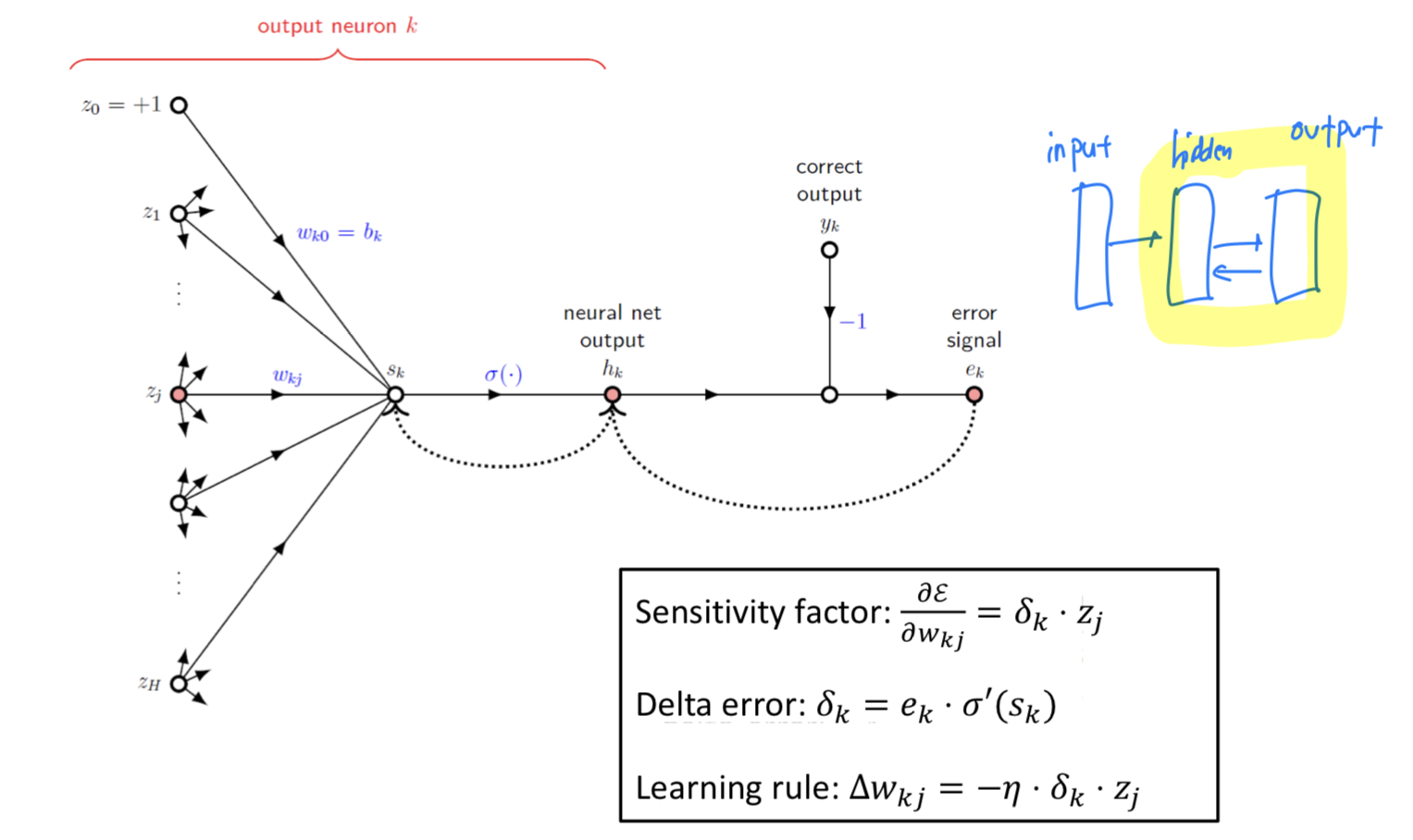
Backward Phase (Output Layer)

Chain Rule

• Two differentiable function $f$ and $g$
  

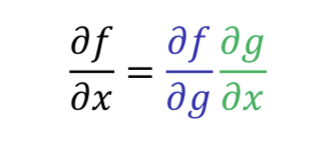
Sensitivity & Delta Error

• Hidden-to-output layer의 상황에서 계산의 편의를 위해 ($k-th$) node만 고려한다.
  

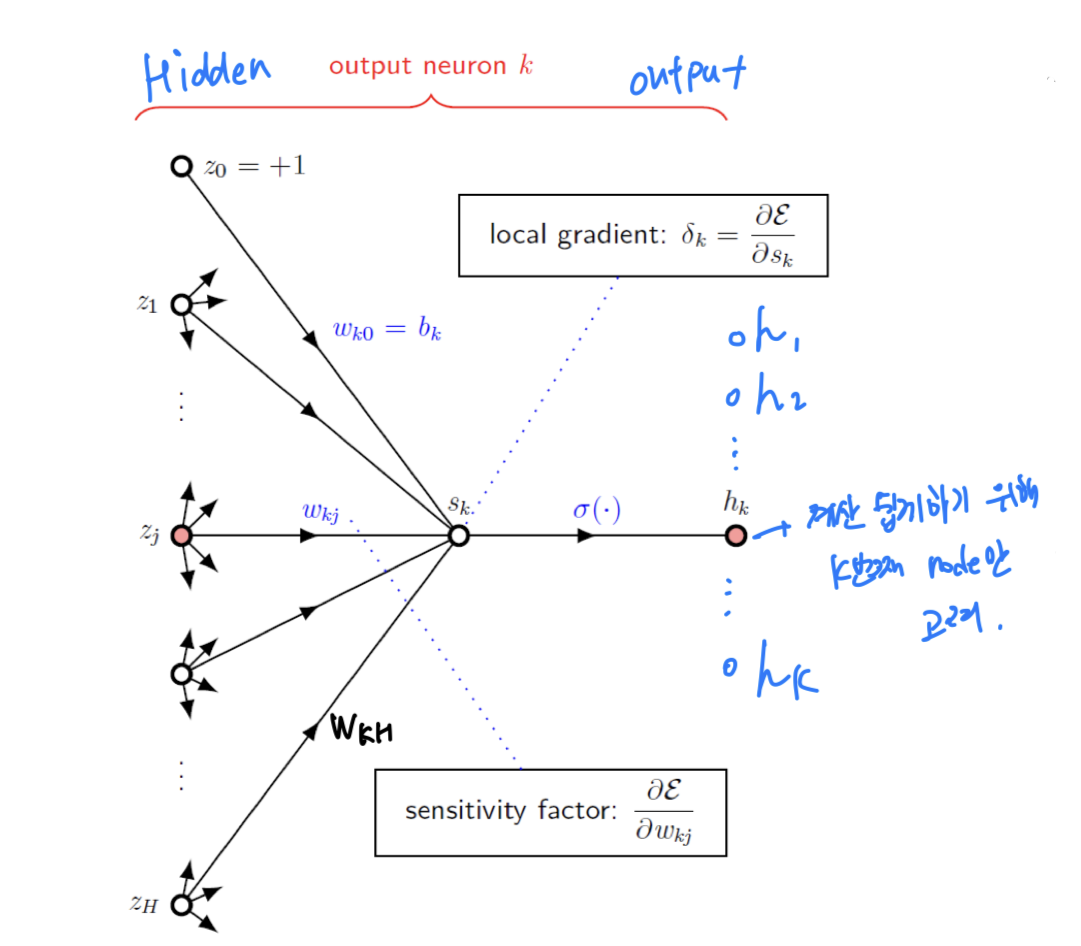
  • Delta Error : Determine scale (크기 결정)
    
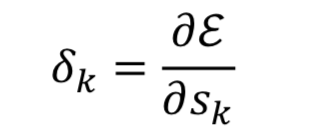
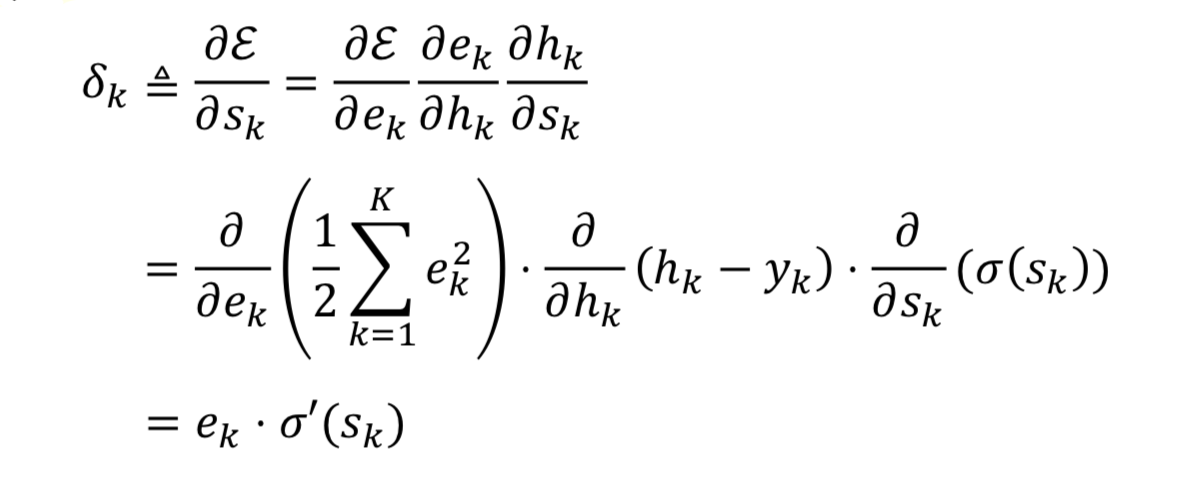
  • Sensitivity : Determine direction (방향 결정)
    node들에 대한 지분
    

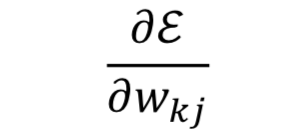
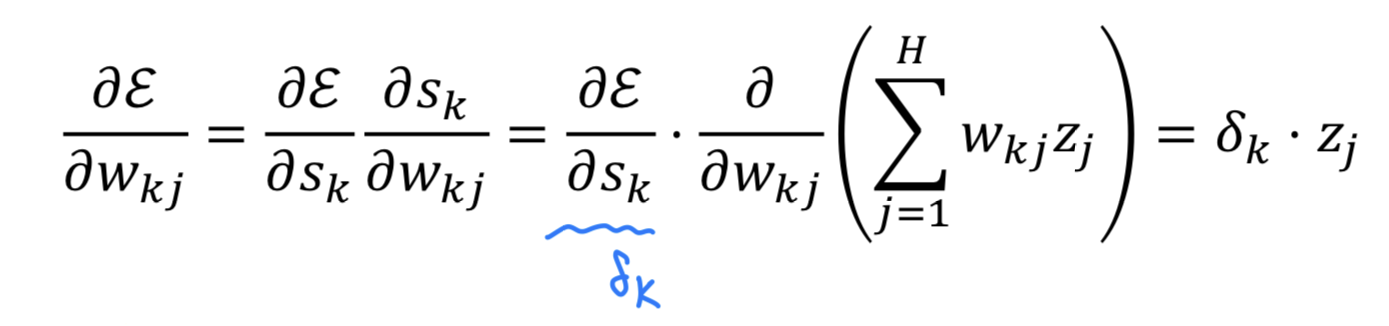
• Weight update rule : $w_{kj}$ ⬅️ $w_{kj}$ + $\Delta w_{kj}$
  

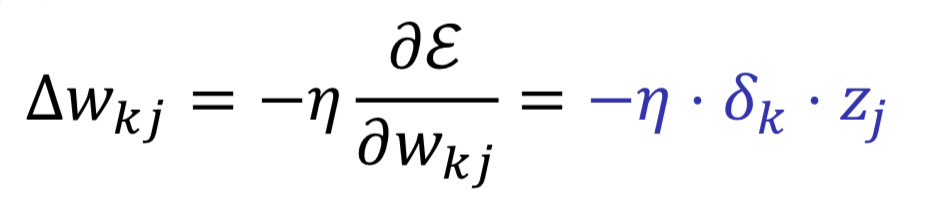
  • $\eta$ : Learning Rate

Summary

Backward Phase (Hidden Layer)

• Hidden-to-output layer의 상황에서 계산의 편의를 위해 ($k-th$) node만 고려한다.
  
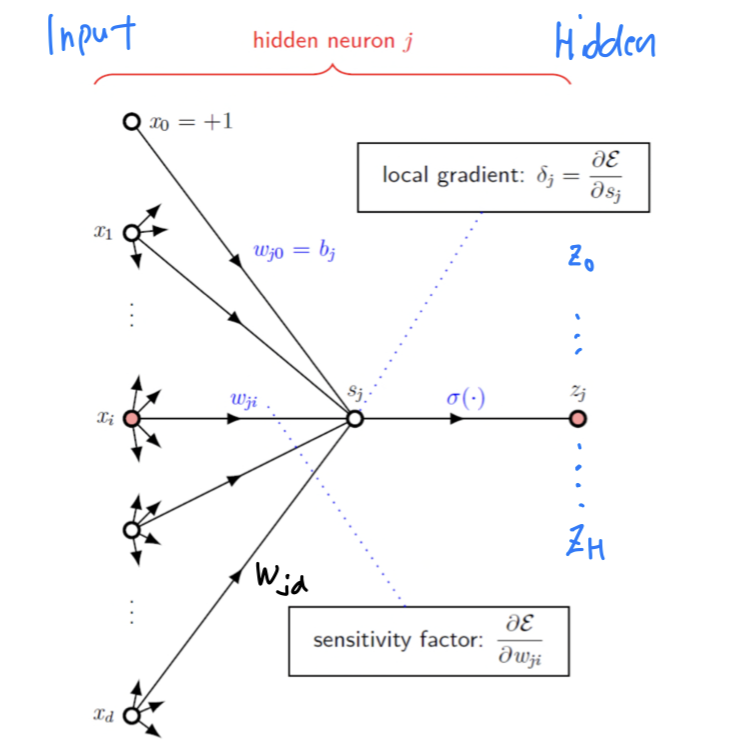
  • Delta Error : Determine scale (크기 결정)
    
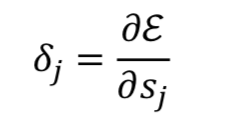
  • Sensitivity : Determine direction (방향 결정)
    node들에 대한 지분
    

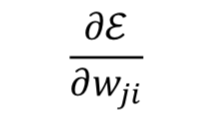
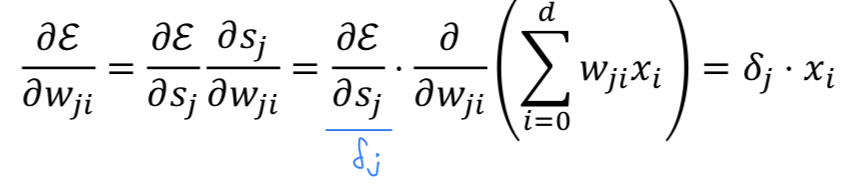
• Weight update rule : $w_{kj}$ ⬅️ $w_{kj}$ + $\Delta w_{kj}$
  
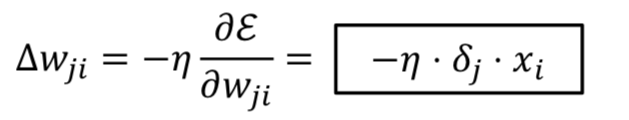
  • $\eta$ : Learning Rate

Summary

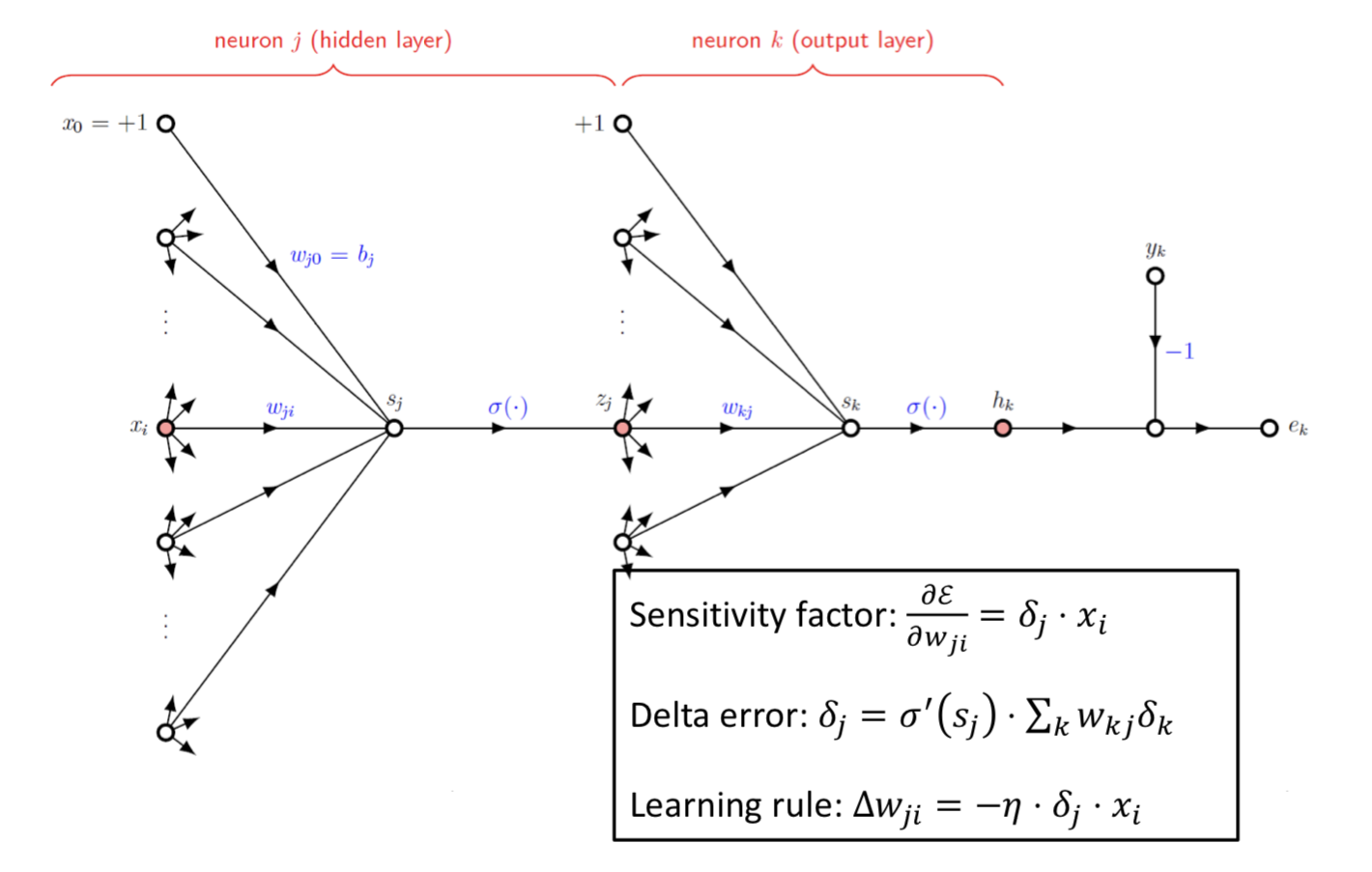
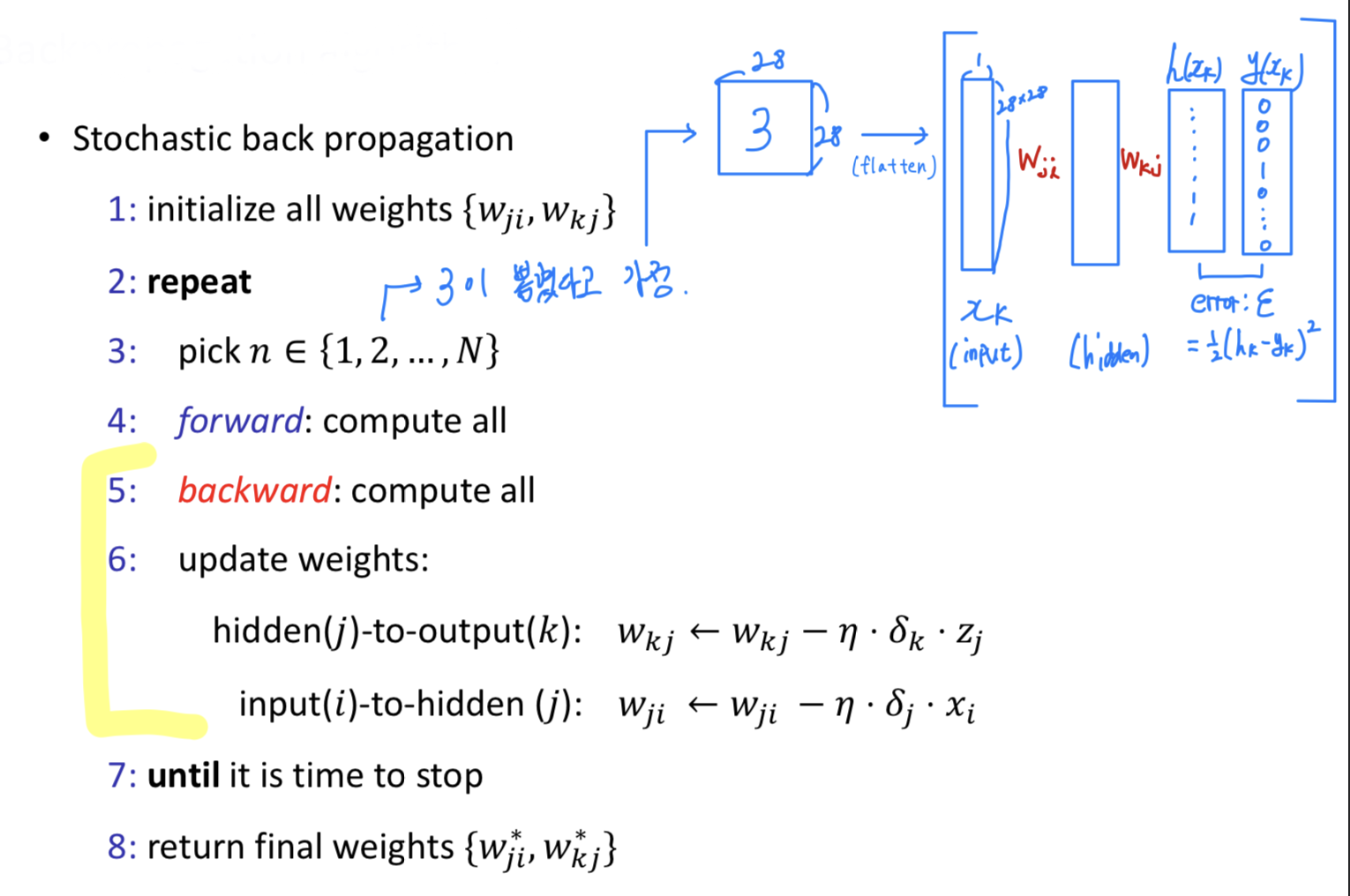
Backpropagation Algorithm

---

Deep Learning : Motivation

Neural network : poweful model

• Universal approximators
  

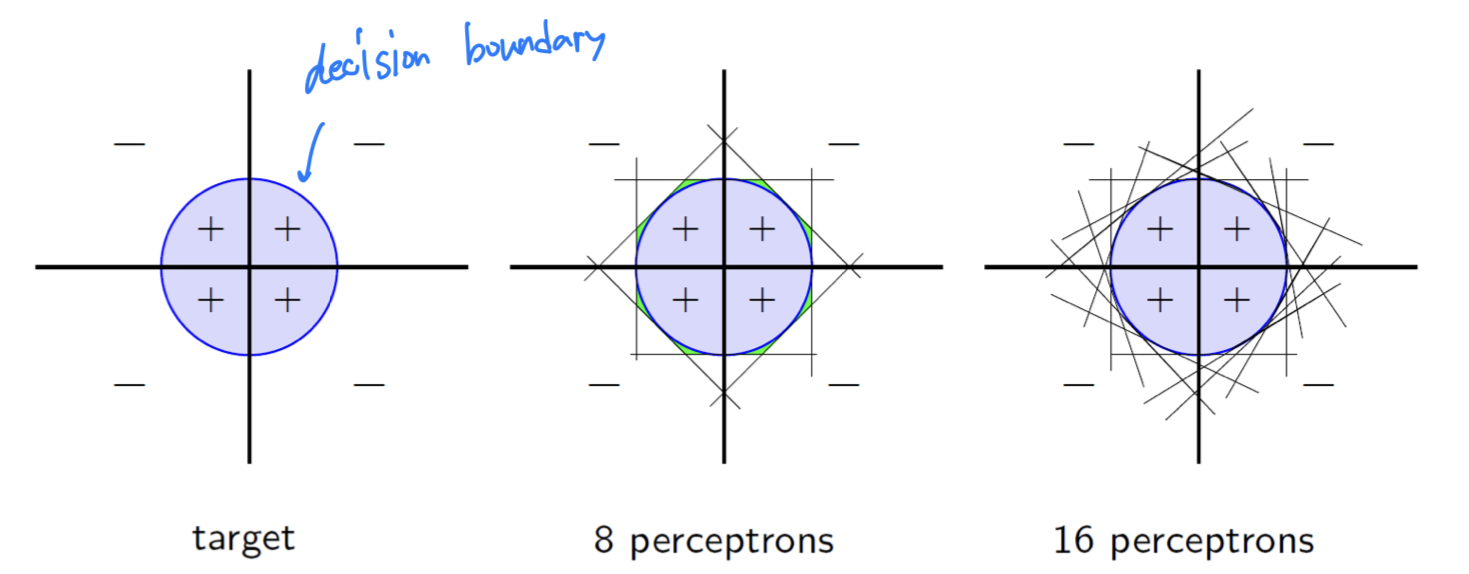
  • Perceptron 하나로는 Non-Linear 형태의 함수를 근사할 수 없다.
  • 따라서 Multiple Perceptron을 사용하면,
    Non-linear 형태를 근사할 수 있는 function이 된다.
    ➡️ 그렇기 때문에 ANN을 Universal Function Approximator라고 한다.

• 일반적으로 More Layer, More Intelligent
  (하지만 항상 그런 것은 아니다)
  (data가 충분히 뒷받침되어야 하고, data의 quality가 좋아야 하고, 좋은 algorithm이 있어야 하고, ...)

• Human brain : at least 5 ~ 10 layers for visual processing

Still have a Problem

• Vanishing gradient, overfitting, runtime ...
  ➡️ breakthrough(돌파구) : backpropagation, unsupervised pretraining, ...

vanishing gradient

• Layer가 깊어진다면, Error가 input layer까지 잘 전달이 되지 않을 것이다.
  

Rectifier (ReLU)

• Activation Function으로 ReLU를 사용하면,
  Signal이 양수인 구간에서는 gradient vanishing 문제를 해결할 수 있다.
  
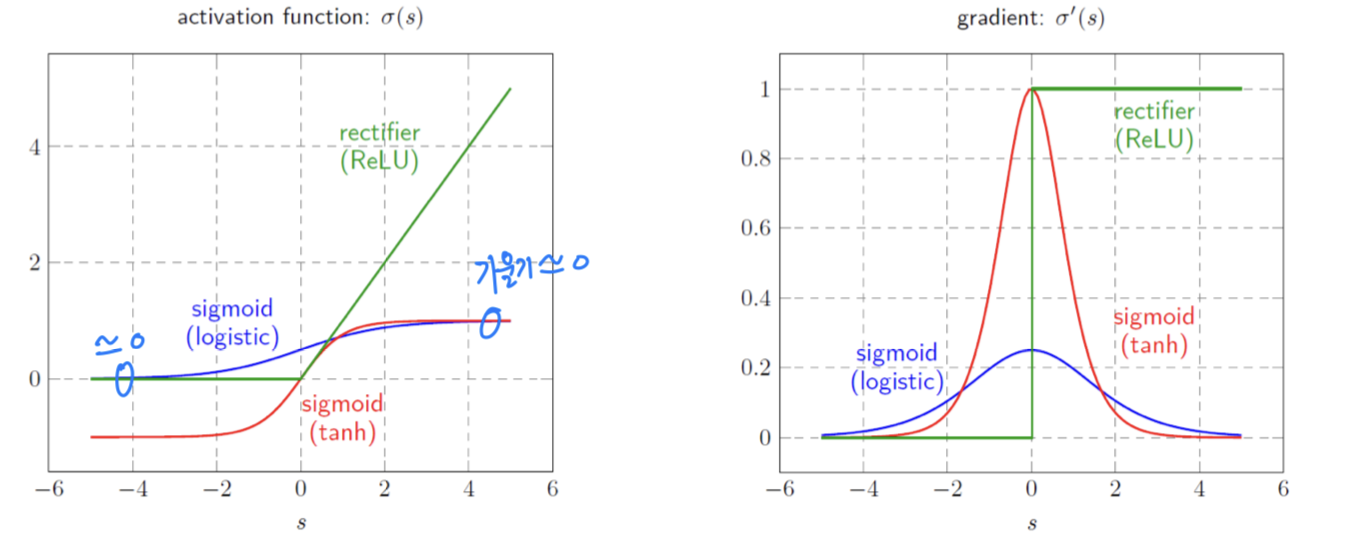
  • Logistic : suffers from the vanishing gradient problem
  • Tanh : better than logistic but the problem exits
  • Rectifier(ReLU) : gradients do not vanish