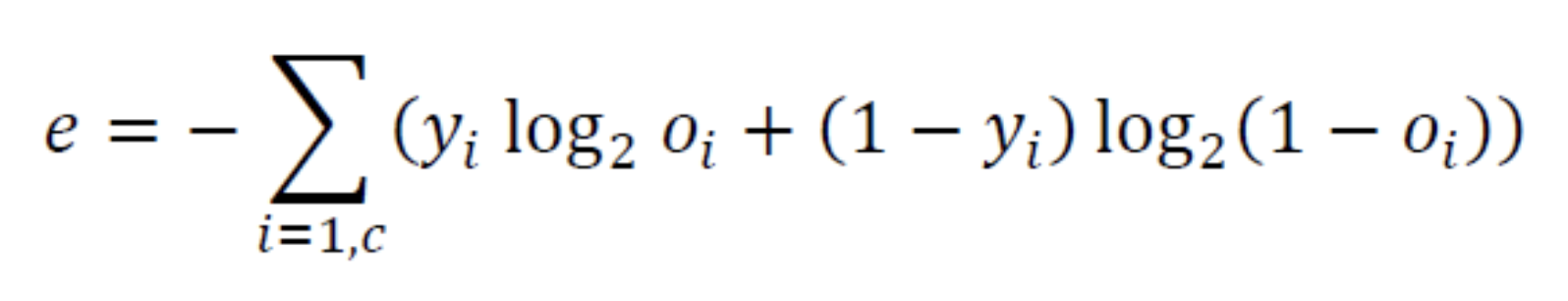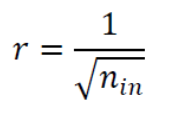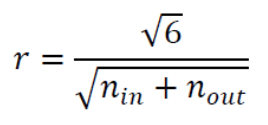[Chap 5] 딥러닝 최적화

Hyungseop Lee·2023년 5월 8일

[Study] Machine Learning

목록 보기

9/9

목적함수 : Cross Entropy & Log Likelihood

MSE 단점

MSE(평균제곱 오차) : $e = \frac{1}{2} ||y - o||_2^2$ ( $y$ : target, $o$ : 실제 output)
신경망의 output $o$ 가 target값 $y$ 와 같을 때 0이 되고,
둘의 차이가 크면 클수록 커지므로 $e$ 는 벌점으로서 훌륭하다.
하지만 학습 과정 전체를 놓고 따져보면 문제가 생긴다.

MSE가 목적함수로서 부적절한 상황

단순한 신경망 예제를 살펴보자.
- 우선 신경망 학습 과정에서의 벌점은 오류를 줄이는 방향으로 weight와 bias를 교정하는 작업이므로,
  gradient가 벌점에 해당한다고 할 수 있다.
  (아래 예제에서 Activation Function으로 Sigmoid를 사용)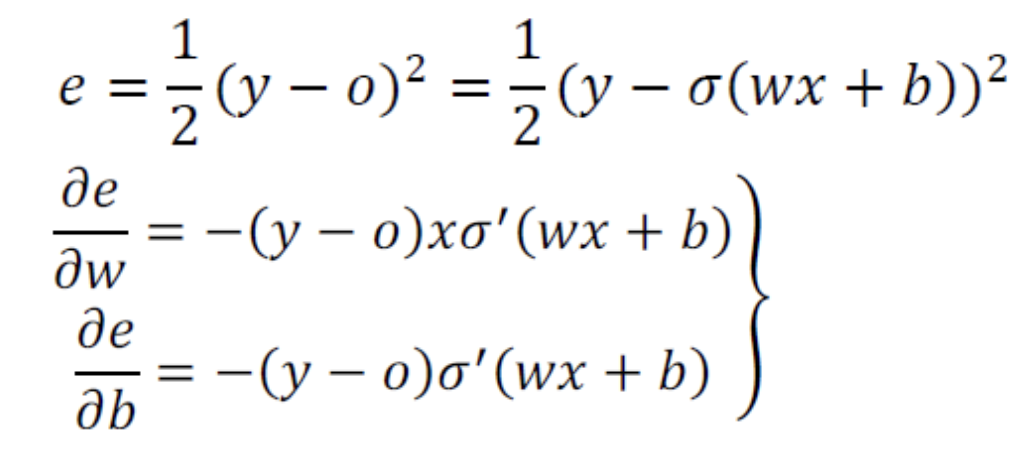
- 왼쪽 신경망에서 Sample $x$ 에 대한
  target $y$ = 0.0
  예측값 $o$ = 0.7503
  $\frac{\partial e}{\partial w} = 0.2109$
  $\frac{\partial e}{\partial b} = 0.1406$
- 오른쪽 신경망에서 Sample $x$ 에 대한
  target $y$ = 0.0
  예측값 $o$ = 0.9971
  $\frac{\partial e}{\partial w} = 0.0043$
  $\frac{\partial e}{\partial b} = 0.0029$
  
  오른쪽 신경망의 오류가 더 크기 때문에 더 벌점을 받아야 하지만
  오른쪽 신경망의 gradient값이 더 작아졌다.
  결국 더 많이 틀린 오른쪽 상황에 더 낮은 벌점을 주는 꼴이 되었다.
왜 이런 현상이 발생했는가?
다음은 Sigmoid 함수와 도함수를 보여준다.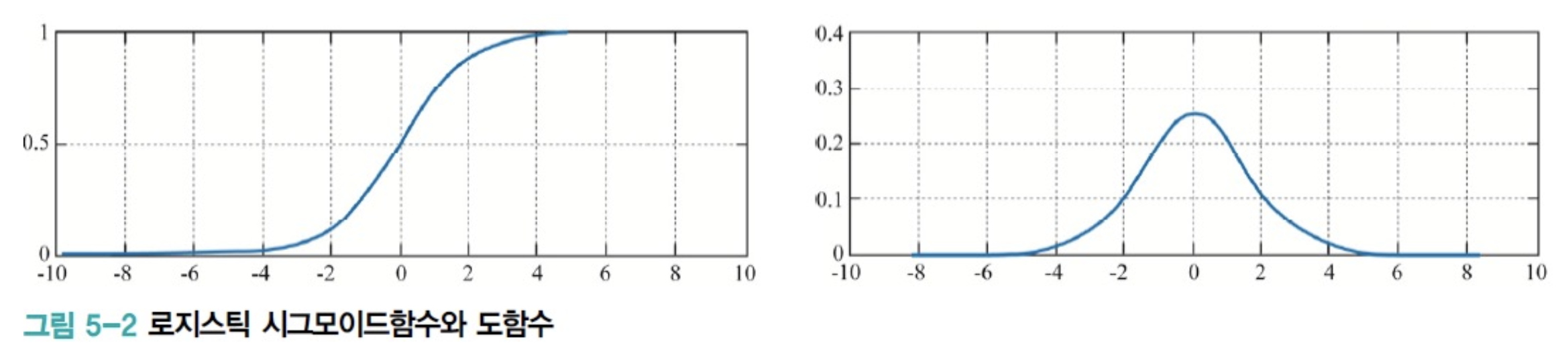
도함수는 입력값이 0일 때 가장 크고, 입력값이 커지거나 작아지면 0에 수렴한다.
그런데 Sigmoid 도함수 $\sigma'(wx+b)$ 가 gradient 구하는 과정에 포함되어 있기 때문에
$wx+b$ 가 커질수록 gradient가 작아지는 것이다.
따라서 오차가 커질수록 gradient가 작아진다
이러한 현상은 느린 학습의 원인이 된다.
딥러닝에서 더딘 학습은 심각한 문제가 된다.

Cross Entropy

앞에서 설명한 바와 같이 MSE를 목적함수로 사용하면 더딘 학습 현상이 발생.
따라서 딥러닝은 MSE 대신 Cross Entropy를 주로 사용.
Cross Entropy에 대해 Chap2에서 정리했었음
(간단히 말하면, 서로 다른 두 확률분포 P와 Q 사이의 entropy)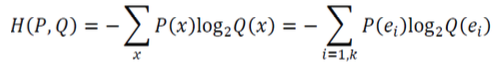
여기서는 신경망의 출력 $o$ = $Q(y)$ 과 정답 label $y$ = $P(y)$ 를 이용해 목적함수를 구하므로
$y$ 가 확률변수 역할을 한다.
따라서 식을 다음과 같이 바꿔 쓸 수 있다. ( $y \in {0, 1}$ 라고 가정)
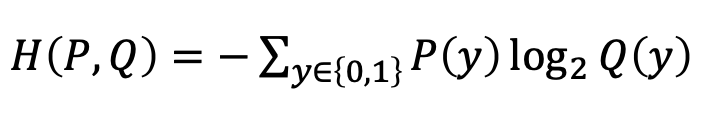
label $y$ 가 0일 때와 1일 때의 $P, Q$ 의 확률분포는 다음과 같다.
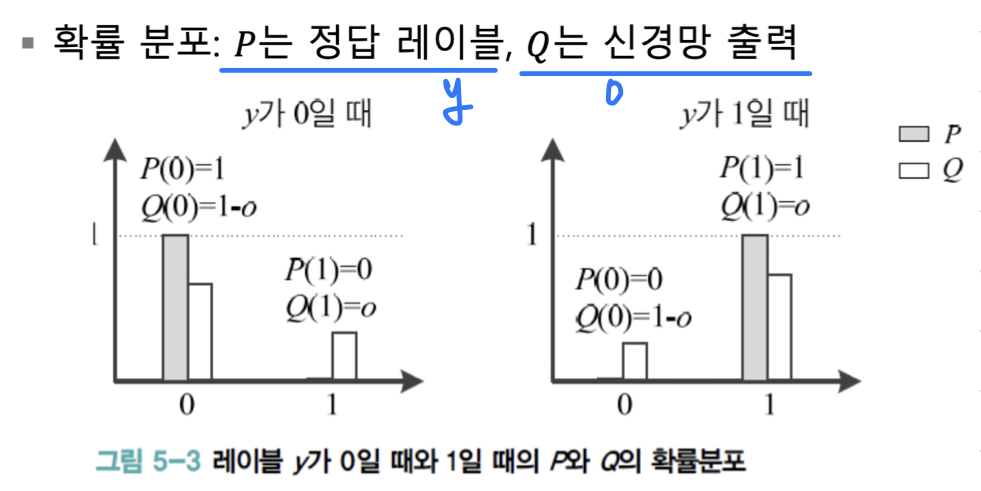
위의 분포를 다음의 수식으로 통일할 수 있다
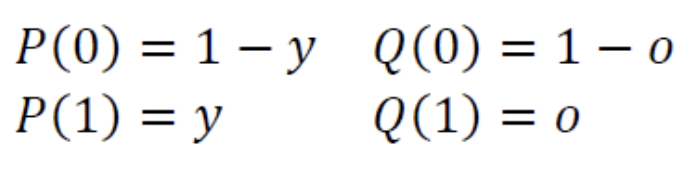
위 식을 토대로 Cross Entropy 목적함수를 쓰면 다음과 같다.
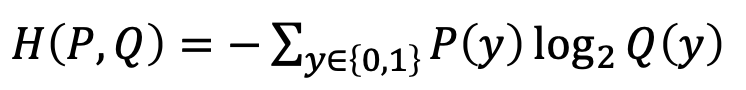
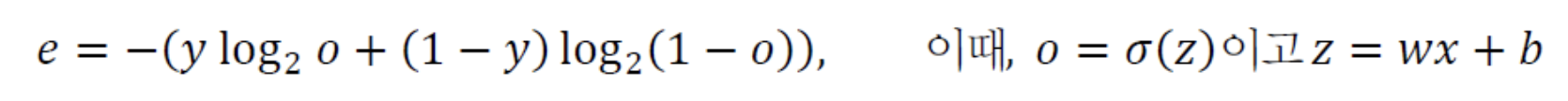
과연 목적함수로 Cross Entropy를 사용했을 때가
MSE를 썼을 때의 단점을 해결했을까?
- 우선 목적함수로서 역할을 하는지 == 예측이 잘 안됐을 때 error가 큰지? 를 확인해보자
- MSE에서 나타난 느린 학습 문제를 해결하는지? 를 확인해보자
  아래에서 볼 수 있듯이, 오류가 더 큰 오른쪽 상황에
  더 큰 gradient가 발생함을 확인할 수 있다
  다시 말해, Cross Entropy를 사용하면 오류가 클수록 더 큰 벌점을 부과하는 것이다.

c개의 출력 node를 가진, 즉 출력 벡터 $o$ 를 출력하는 신경망으로 확장하면 다음의 식이 된다.

Softmax

지금까지는 은닉층과 출력층 모두 같은 Activation Function을 사용한다고 가정하고 수식을 유도했다.
하지만 몇 가지 이유 때문에 출력 node는 softmax Activation Function을 사용하기도 한다.
softmax :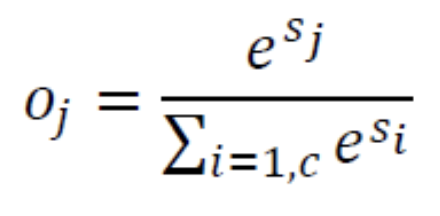
다음은 출력 node가 3개인 간단한 신경망에 대해 Sigmoid와 softmax Activation Function을 비교한다.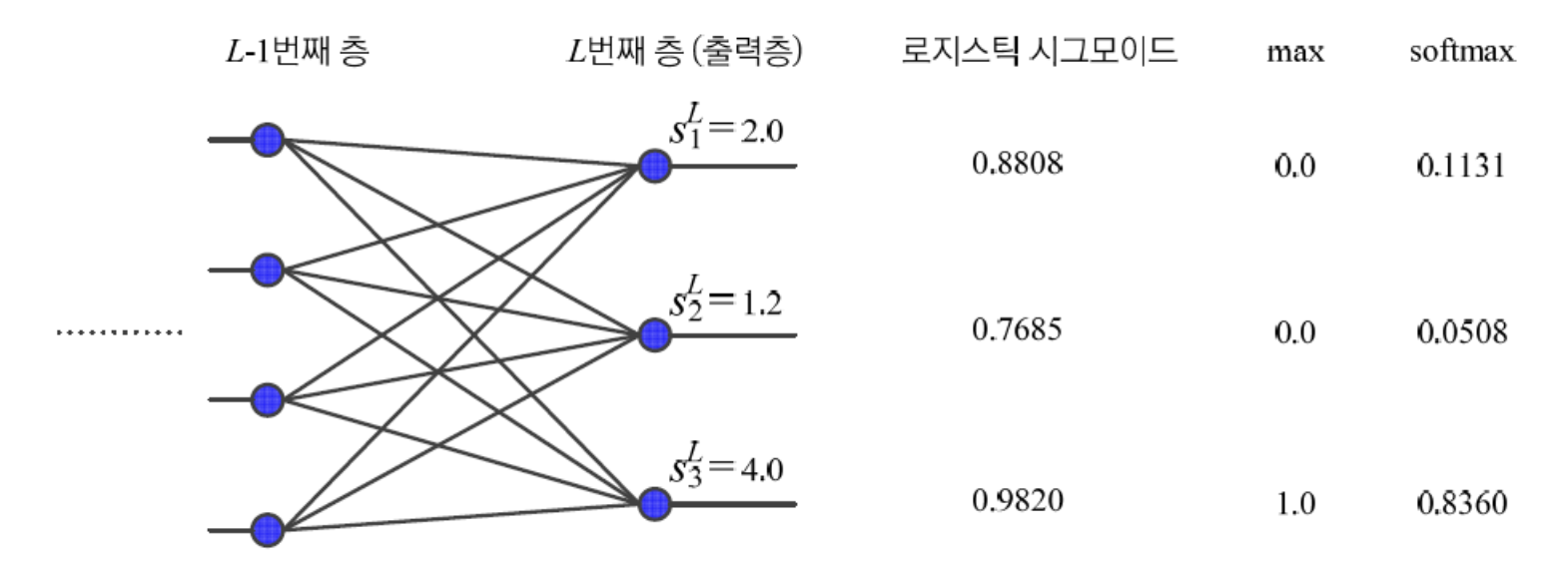
- $s_1, s_2, s_3$ 가 각각 2.0, 1.2, 4.0일 때,
- Sigmoid는 0.8808, 0.7685, 0.9820을 출력한다.
- Softmax는 0.1131, 0.0508, 0.8360을 출력한다.
  ➡️ Softmax는 최대값을 더욱 활성화하고 작은 값을 억제하는 효과를 보인다.
  ➡️ 또한 Softmax는 출력값을 모두 더하면 1.0이 되는 특성이 있다.
  이 성질에 따라 softmax의 출력을 확률분포로 취급하면 여러 가지 목적에 유용하게 사용할 수 있다.
  (예를 들어, softmax의 출력을 보고 가장 큰 값이 미리 정해 놓은 임곗값보다 작거나,
  가장 큰 값과 두 번째 큰 값의 차이가 임곗값보다 작으면 분류를 포기하고 기각하는 전략을 쓸 수 있다.)

Log Likelihood

Log Likilihood(로그우도) : 딥러닝에서 널리 쓰이는 또 다른 목적함수인 로그우도이다.
로그우도는 모든 노드값을 고려하는 MSE나 Cross Entropy와 달리 $o_y$ 라는 하나의 노드값만 본다.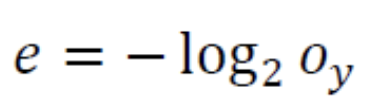
- 이 식에서 $o_y$ 는 Sample의 label에 해당하는 node의 출력값을 뜻한다.
- 다음 예제에서는 3개의 출력 node를 갖는 신경망에서 Softmax Activation Func을 사용한다고 가정한다.
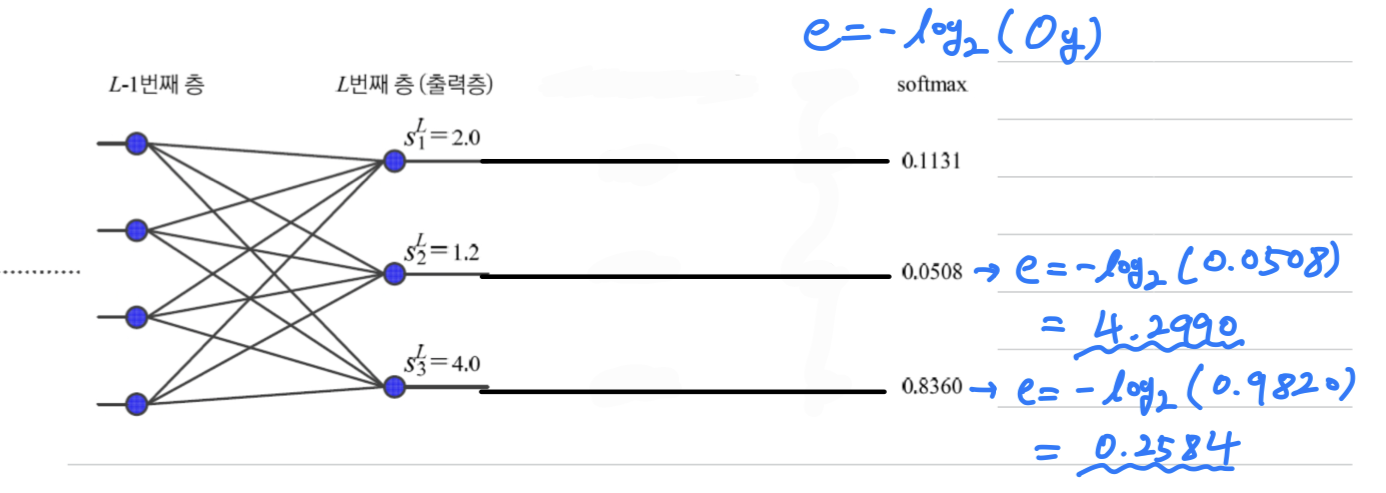  ➡️ $o_y$ 가 1.0에 가까워질수록 $e$ (오류)가 크게 줄어든다

Softmax는 최대값이 아닌 값을 억제하여 0에 가깝게 만든다는 의도를 포함한다.
따라서 학습 Sample이 알려주는 부류에 해당하는 출력 node값만 보겠다는 로그우도 목적함수와 잘 어울린다.
이러한 이유로 딥러닝에서는
종종 softmax activation function과 로그우도 목적함수를 결합하여 사용한다.
물론 softmax activation function과 MSE 또는 Cross Entropy를 결합해 사용해도 된다.
어떤 목적함수가 가장 좋은 성능을 보일지 확인하려면 데이터로 실제 실험을 하는 것이 최선이다.

성능 향상을 위한 요령

최저점을 아무리 빨리 정확하게 찾아도, Overfitting에 해당한다면 아무 의미가 없다.
따라서 Overfitting을 방지하여 일반화 능력을 극대화하는 전략이 필요하다.
Overfitting 방지책에 대해서는 추후 momentum과 adaptive learning rate 기법에서 배운다.

한 가지 꼭 기억할 점은 momentum과 adaptive learning rate 기법들은
heuristic(경험규칙)에 불과한 것이라는 사실이다.
따라서 자신에게 주어진 문제와 data에 잘 들어맞을지는 실험을 통해 신중하게 확인하는 수밖에 없다.

데이터 전처리

data가 $(키, 몸무게, 혈압)^T$ 형태로 주어졌다. 키는 $m$ , 몸무게는 $kg$ 단위라면
$(1.855, 65.5, 122)^T$ 와 같은 Sample이 있다고 하자.
위 data는 feature마다 규모가 달라 문제가 발생할 수 있다.
1. 키라는 첫 번째 feature에서 1.855라는 값을 가진 사람과 1.525를 가진 사람은
  33cm나 차이나지만 실제 feature값 차이는 불과 0.33밖에 안된다.
2. 또한 두 사람의 몸무게가 65.6와 45.0이라면 20.5라는 차이가 생긴다.
- 1, 2 feature은 대략 100배의 규모 차이가 있다.
  또한 feature값이 양수라는 특성이 있다.
  이러한 data는 수렴 속도가 느려질 수 있다.
모든 feature가 양수만 가질 경우, 학습이 왜 느려지는가?
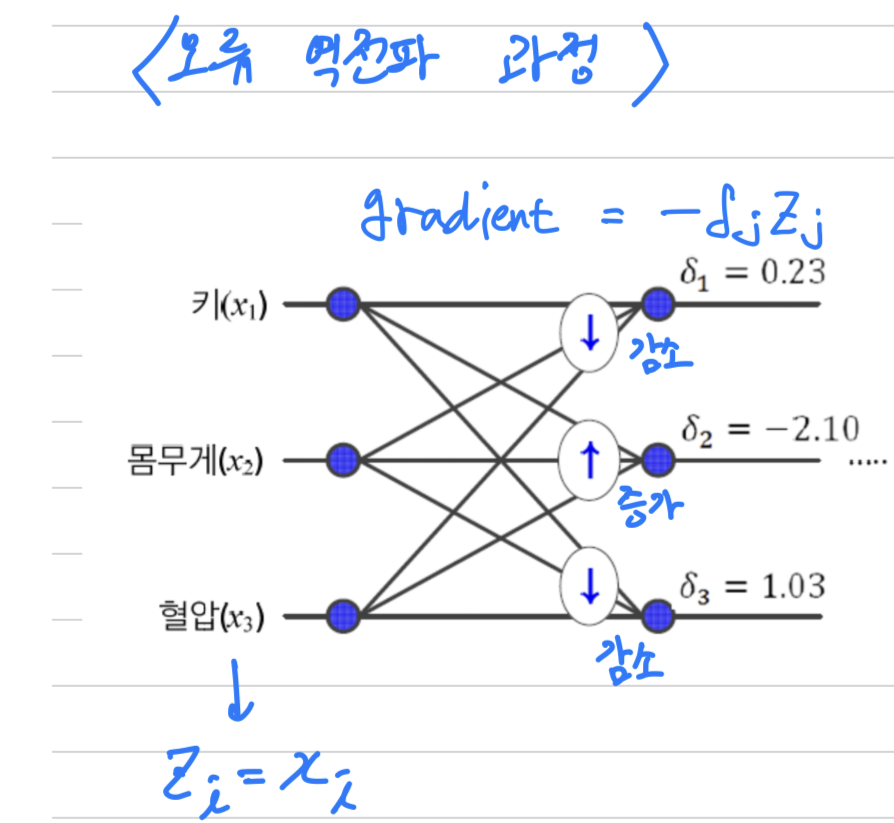
- 이처럼 여러 가중치가 뭉치로 같이 증가하거나 감소하면,
  최저점을 찾아가는 경로가 갈팡질팡하게 되며 결국 수렴 속도 저하로 이어진다.
  ➡️ 이 문제를 해결하기 위해 feature값의 평균이 0이 되도록 변환을 수행 (1)하면 된다.
- 이제 키와 몸무게의 규모가 달라 발생하는 문제를 생각해보면,
  키는 몸무게보다 규모가 100여 배 작다.
  따라서 Back propagation식에 따르면 $-\delta_jz_j$ 가 gradient이기 때문에
  $x_1$ 에 연결된 모든 가중치는 $x_2$ 에 연결된 가중치보다 100여 배 느리게 학습이 진행된다.
  ➡️ 이 문제를 해결하기 위해 모든 feature의 표준편차를 1.0으로 통일 (2)하면 된다.

정규화

(1), (2) 이 두가지 변환을 동시에 수행하는 것을 정규화(Normalization)이라고 한다.
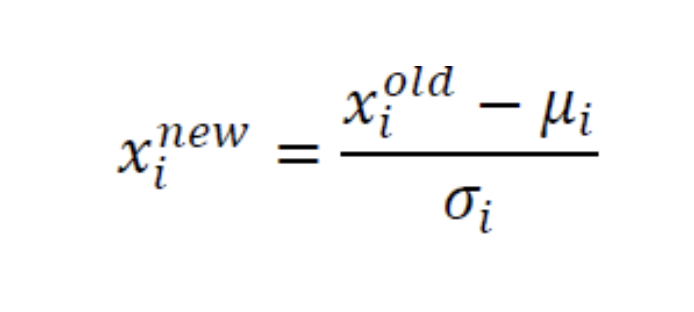
- $x_i^{old}$ : 원래 feature값
- $x_i^{new}$ : 변환된 feature값 == Z-Score == 표준점수
- $\mu_i$ : $i$ 번째 feature의 평균
- $\sigma_i$ : $i$ 번째 feature의 표준편차
  
  ➡️ 의사결정 과정에서 어떤 feature가 다른 feature보다 더 중요하게 작용한다는 사실을 알고 있다면, 이 정보를 규모 조절에 활용할 수 있다.
  이때 더 중요한 feature의 표준편차가 덜 중요한 feature보다 크도록 변환하면 된다.

One-Hot Encoding

$(키, 몸무게, 혈압)$ 의 3차원 feature vector에 성별과 체질이 추가되어 5차원이 되었다고 가정하자.
$(키, 몸무게, 혈압, 성별, 체질)$
- 남자 1, 여자 2
- 태양인 1, 태음인 2, 소양인 3, 소음인 4
  
  예를 들어, (1.855, 65.5, 122, 1, 3)은
  키가 1.855m, 몸무게 65.6kg, 혈압 122인 소양인 남자라는 Sample이다.
  
  그런데 성별과 체질에 정수 코드를 부여한 일은 편의상 한 것에 불과하며,
  이처럼 크기 개념을 가지지 않은 값을 명칭 값(nominal value)라고 한다.
  즉, 체질이 1인 사람이 체질 4인 사람보다 체질 2인 사람에 더 가깝다고 말 할 수 없다.
  
  ➡️ 따라서 명칭값을 가진 data는 one-hot방식의 코드로 변환한다.
  
  성별은 두 가지 값을 가지므로 두 비트,
  체질은 네 가지 값을 가지므로 네 비트로 변환한다.
  이 비트열은 feature값에 대응하는 한 비트만 1이고 나머지는 모두 0이다.

가중치 초기화

신경망의 가중치는 난수를 생성하여 초기화해야 한다.
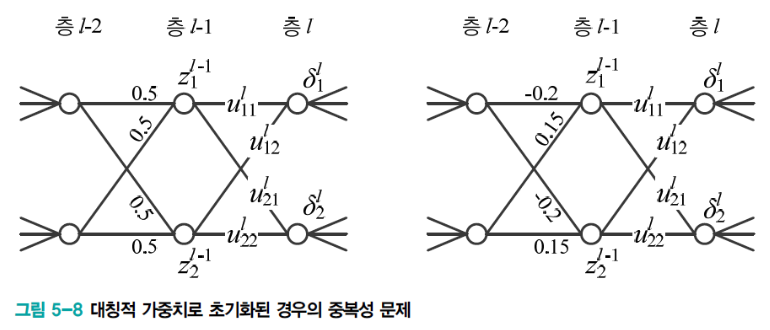
- 왼쪽 그림은 모든 가중치를 0.5로, 오른쪽 그림은 같은 난수 열로 설정한 경우이다
- 이러한 경우에서 $l-1$ 층의 두 노드 $z$ 값은 값이 같다.
  ( $-\delta_jz_j = \frac{\partial J}{\partial u^l_{ji}}$ 가 gradient기 때문)
- 이렇게 $l-1$ 층의 두 노드는 같은 일을 하는 셈이 되어 중복성 문제가 발생.
- 이러한 대칭적 가중치를 피하는 일을 대칭 파괴(symmetry break)라고 한다.
난수는 Gaussian Distribution에서 추출할 수도 있고,
균일 분포에서도 추출할 수 있다.
➡️ 여러 실험 결과 둘의 차이는 별로 없다고 보고됨
하지만 난수의 범위는 매우 중요하다.
극단적으로 weight가 0에 가깝게 설정된다면 gradient가 매우 작아져 학습이 매우 느려지는 현상이 나타나고,
gradient가 너무 크면 Overfitting에 빠질 위험이 있다.
균일 분포를 사용할 때 난수의 범위를 결정하는 Heuristic에는 여러 가지가 있는데,
여기서는 보편적으로 사용하는 두 가지를 제시한다. $n_{in}$ : node로 들어오는 edge 개수,
$n_{out}$ : node에서 나가는 edge 개수
- 1, 2에서 $r$ 을 결정한 후 $[-r, r]$ 범위의 난수를 생성
  ➡️ 표준편차가 $\frac{1}{\sqrt n_{in}}$ 인 정규분포로 초기화
  ➡️ 너무 크지도 않고 작지도 않은 weight를 사용하여 gradient가 vanishing하거나 exploding하는 문제를 막음.
- bias는 weight와 달리 어떤 방식을 사용하든 크게 문제되지 않는다.
  weight와 같은 방식으로 난수로 설정해도 되고, 어떤 상수로 설정해도 좋다.
  bias는 보통 0으로 초기화환다.

여러가지 가중치 초기화 방법들이 존재한다.
- Saxe2014 : weight vector가 수직이 되도록 설정
- Sussilo2014 : random walk(임의 행로) 활용하여 설정
- Sutskever2013 : weight 초기화와 momentum을 동시에 최적화
- Mishikin2016 : weight 분포가 아니라 node의 출력값 분포가 일정하도록 강제화

Momentum

현대 기계학습은 Train Set을 가지고 gradient를 추정하므로 noise가 섞일 가능성이 크다.
따라서 gradient에 smoothing을 가하면 수렴 속도를 개선할 수 있다.
이러한 아이디어에 따른 방법이 Momentum이다.
Momentum은 속도를 나타내는 벡터 $v$ 를 사용하여 현재 gradient를 smoothing한다.
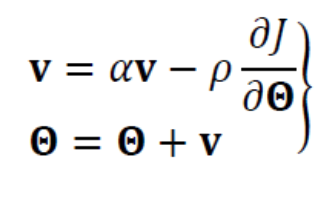
- 속도 벡터 $v$ 는 이전 gradient를 누적한 것으로 볼 수 있다.
  또한 $\alpha$ 는 [0, 1]범위이고, $\alpha$ 를 0으로 설정하면 이전 gradient 정보를 전혀 사용하지 않는 기존 수식과 같아진다.
  즉 1에 가까워질수록 이전 gradient 정보에 큰 weight를 주는 셈이 되고
  $\Theta$ 가 그리는 궤적은 매끄러워진다.
- 보통 $\alpha$ 는 0.5, 0.9, 0.99를 사용한다.
- 또는 처음에 0.5로 시작하고 epoch이 증가함에 따라 점점 키워 0.99에 도달하는 방법을 사용한다.
아래의 그림에서 검은선은 momentum을 적용하지 않았을 때 Gradient Descent가 최적해를 찾아가는 과정을 보여 준다.
파란선은 momentum을 적용했을 때이다.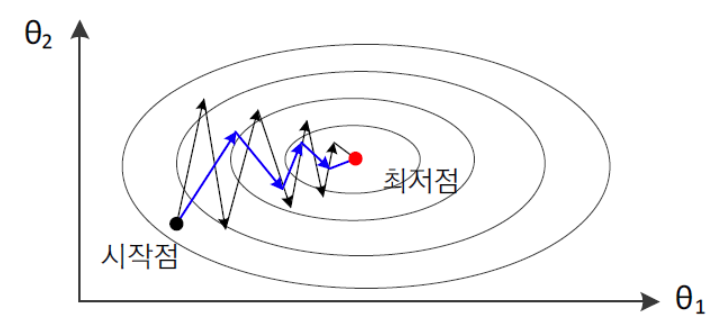
- 검은선(momentum 적용 X)에서 Overshooting 현상을 확인할 수 있다
  ➡️ Overshooting : 이동량이 너무 커 적절한 곳을 지나치는 현상
- 파란선(momentum 적용 O)은 Overshooting 현상이 감소하였고 결과적으로 훨씬 적은 반복 횟수로 최적해를 찾아간다.
현재는 기존 momentum 기법을 개선한 Nesterov momentum(네스테로프 모멘텀) 기법이 널리 사용되고 있다.
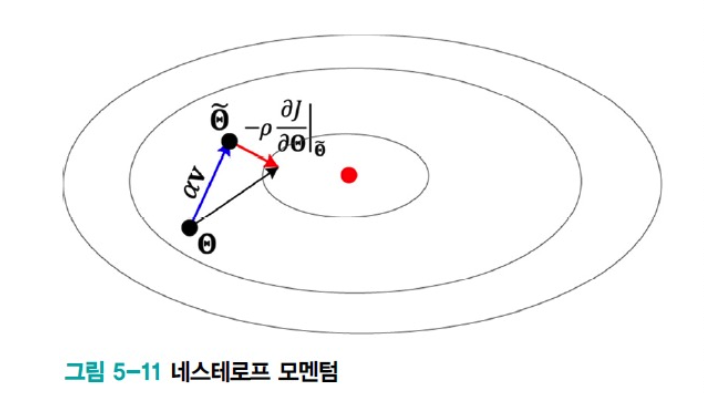
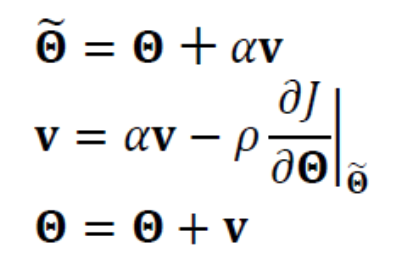
- Nesterov Momentum은
  현재 $v$ 값을 이용하여 다음 이동할 곳 $\tilde{\Theta}$ 을 예견(lookhead)한 후,
  예견한 곳의 gradient를 사용한다.
기존 momentum을 이용한 Gradient Descent
Nesterov Momentum을 이용한 Gradient Descent

Adaptive Learning Rate

아래 그림에서 Learning Rate가 높으면 검은 선으로,
Learning Rate가 낮으면 파란선으로 그려 비교한 것이다.
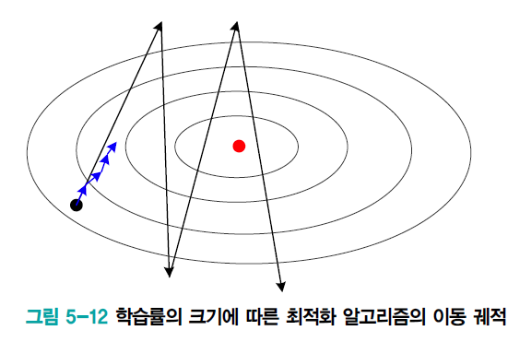
- Learning Rate가 너무 높으면, Overshooting 현상
- Learning Rate가 너무 낮으면, 너무 오랜 시간이 걸림
이러한 Learning Rate의 한계를 극복하기 위한 Adaptive Learning Rate(적응적 학습률)기법이 여러 가지 개발되어 있다.
Adaptive Learning Rate에서는 매개변수마다 자신의 상황에 따라 Learning Rate를 조절해 사용한다.
가장 오래된 기법으로는 바로 이전 Gradient와 현재 Gradient의 부호가 같은 매개변수는
값을 키우고 그렇지 않은 매개변수는 값을 줄이는 전략을 사용한다.
현대 기계 학습은 더 진보한 기법을 사용하는데, 널리 활용되는
AdamGrad, RMSProp, Adam을 공부할 것이다.

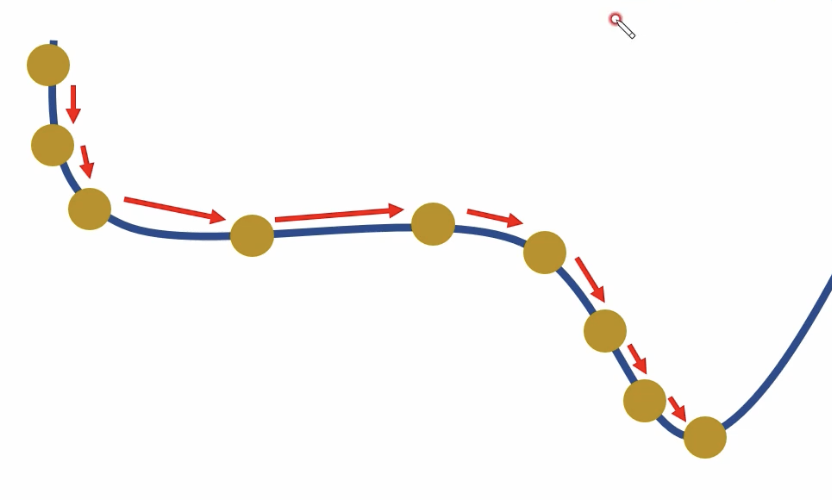
AdaGrad

아래의 알고리즘은 AdaGrad(adpative gradient)를 설명한다.
- 이전 gradient의 누적값( $r$ )이 작으면 많이 이동.
- 이전 gradient의 누적값( $r$ )이 많으면 적게 이동.

RMSProp

AdaGrad는 gradient 누적 vector를 update하는 식을 살펴보면, 단순히 제곱을 더한다.
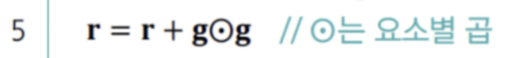
따라서 오래된 gradient와 최근 gradient가 알고리즘이 끝날 때까지 같은 비중의 역할을 한다고 할 수 있다.
결과적으로 $r$ 이 점점 커져 충분히 수렴하지 못한 상황에서 adaptive learning rate가 0에 가까워질 가능성이 있다.
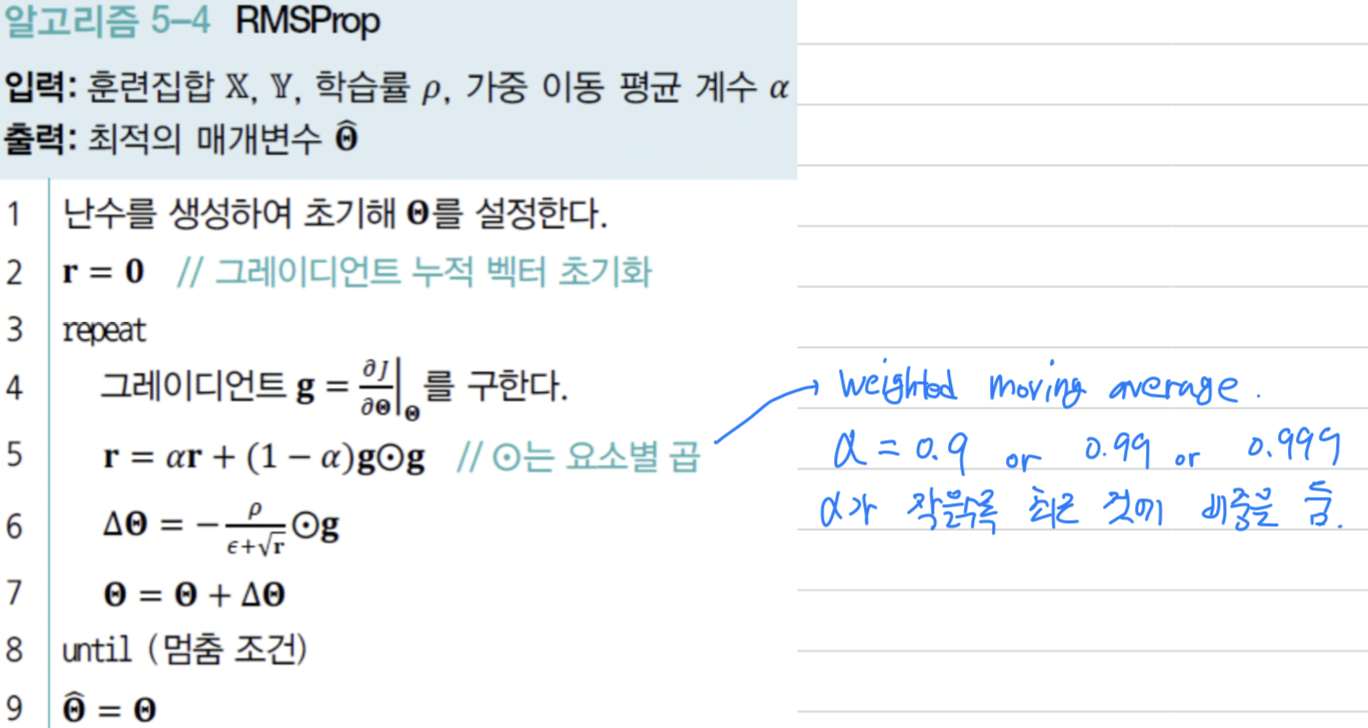
RMSProp은 오래된 gradient의 영향력을 지수적으로 줄이기 위해,
weighted moving average(가중치 이동 평균)기법을 적용한다.
이 기법을 다음과 같이 표현할 수 있다.
$\alpha$ 로 0.9, 0.99, 0.999와 같은 값을 사용한다.

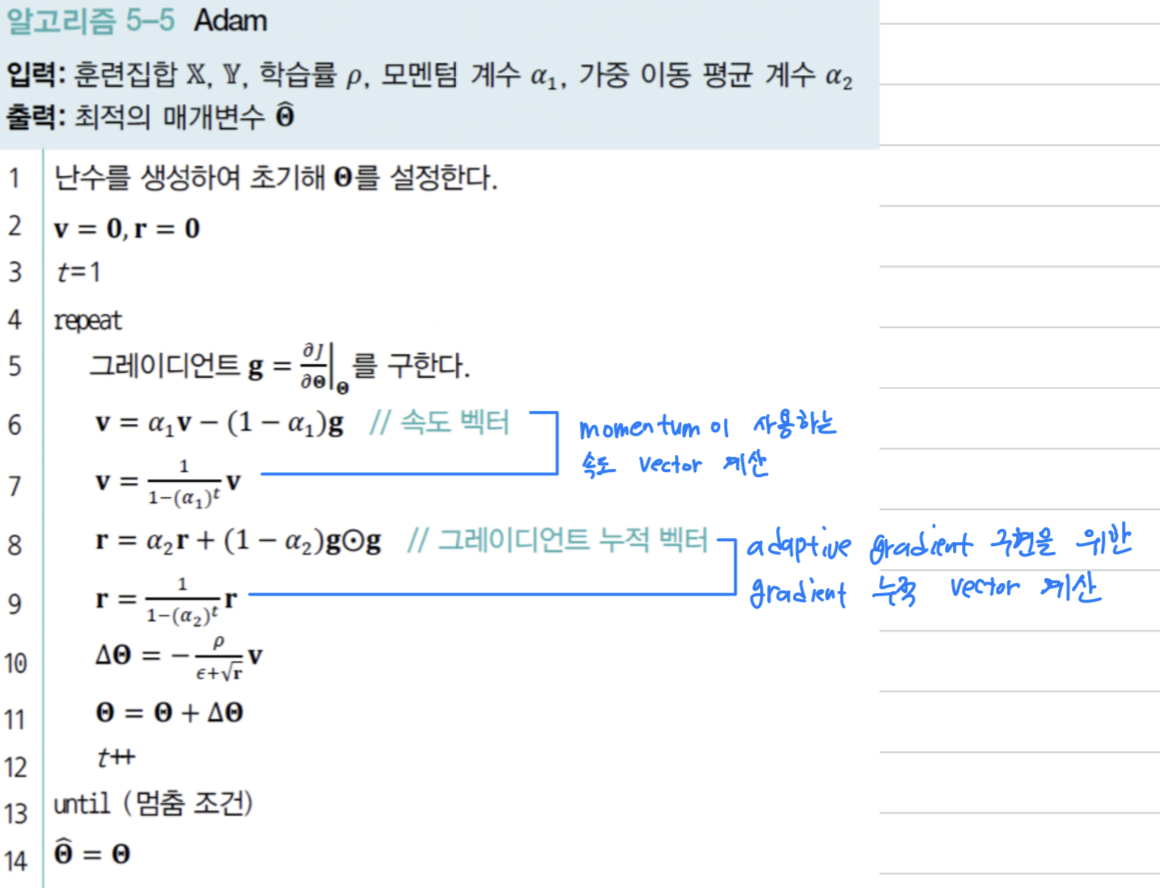
Adam

Adam(Adaptive moment)은 RMSProp에 momentum을 추가로 적용한 알고리즘이다.

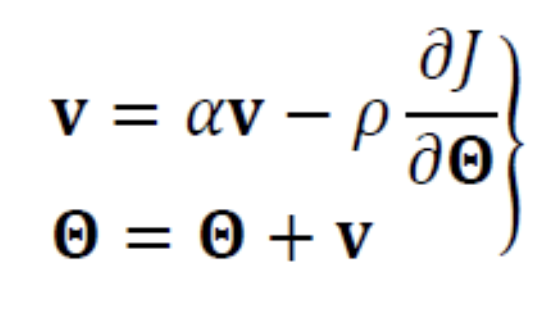
Momentum & Adaptive Learning Rate

https://cs231n.github.io/neural-networks-3/
네 구석에서 중앙으로 급강하 하는 절벽이 형성되어 있고,
중앙에서 동서남북 네 방향으로 길쭉하게 계곡이 있는 협곡 지형이다.
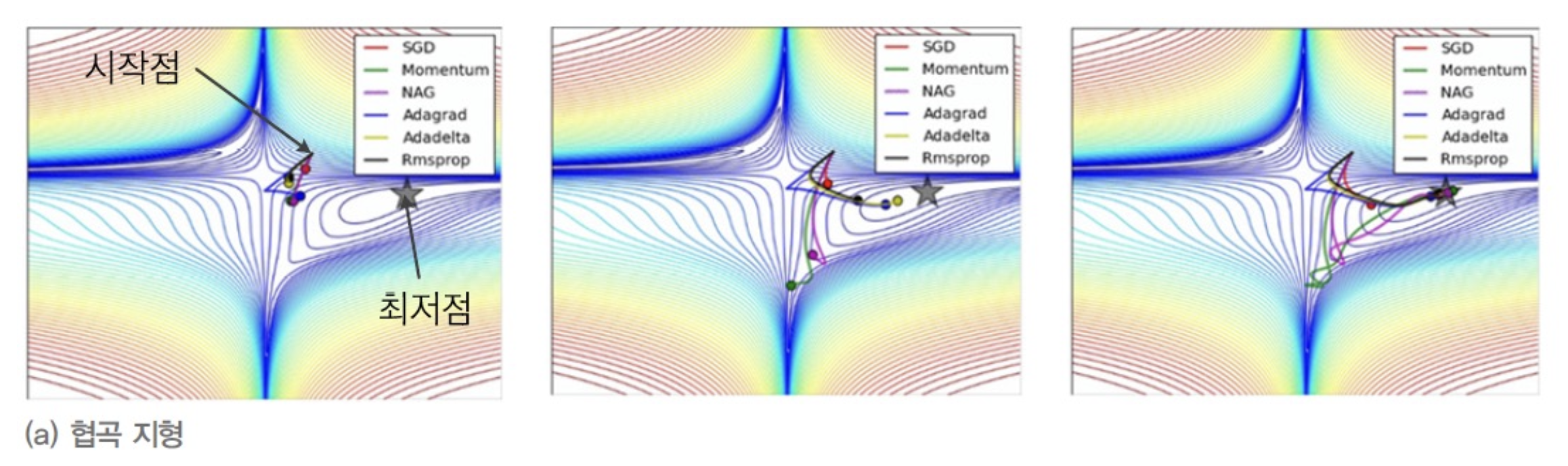
- 두 momentum 기법(Momentum과 NAG(Nesterov Momentum))는 초반에 overshooting이 발생하였는데
  시간이 지나면서 제 방향을 찾아 최저점에 도달.
- 세 Adaptive Learning Rate 기법(AdaGrad, RMSProp, Adadelta)은 비교적 빠른 속도로 최저점에 도달.
- SGD는 매우 느리게 최저점을 도달
중앙 부근에 saddle point(안장점)이 있고 좌우로 절벽, 앞뒤로 고개가 있는 지형이다.
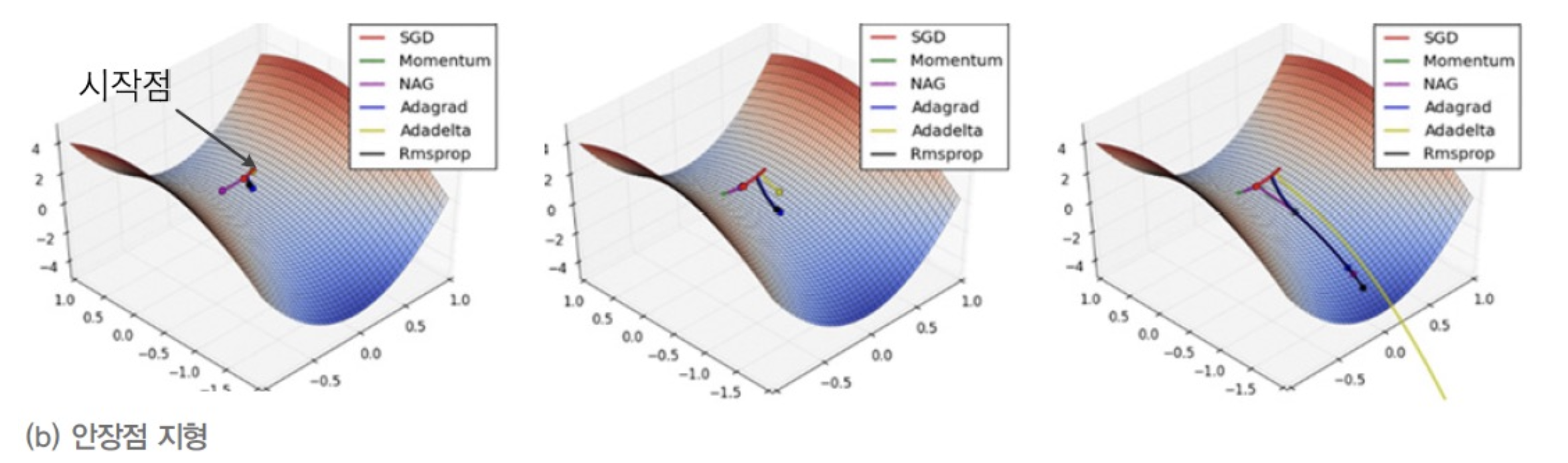
- 두 momentum 기법(Momentum과 NAG(Nesterov Momentum))은 saddle point를 중심으로 진자 운동을 하다가 가까스로 최저점 방향을 찾음
- 세 Adaptive Learning Rate 기법(AdaGrad, RMSProp, Adadelta)은 쉽게 최저점 방향을 찾아 이동.
- SGD는 saddle point를 영원히 벗어나지 못하는 현상을 확인.

이 중 어느 것을 사용해야 할지에 대한 절대적인 기준은 없으니 스스로 실험하고 선택해야 한다.

Activation Function

다음은 시대별로 유행한 대표적인 Activation Function을 보여준다.
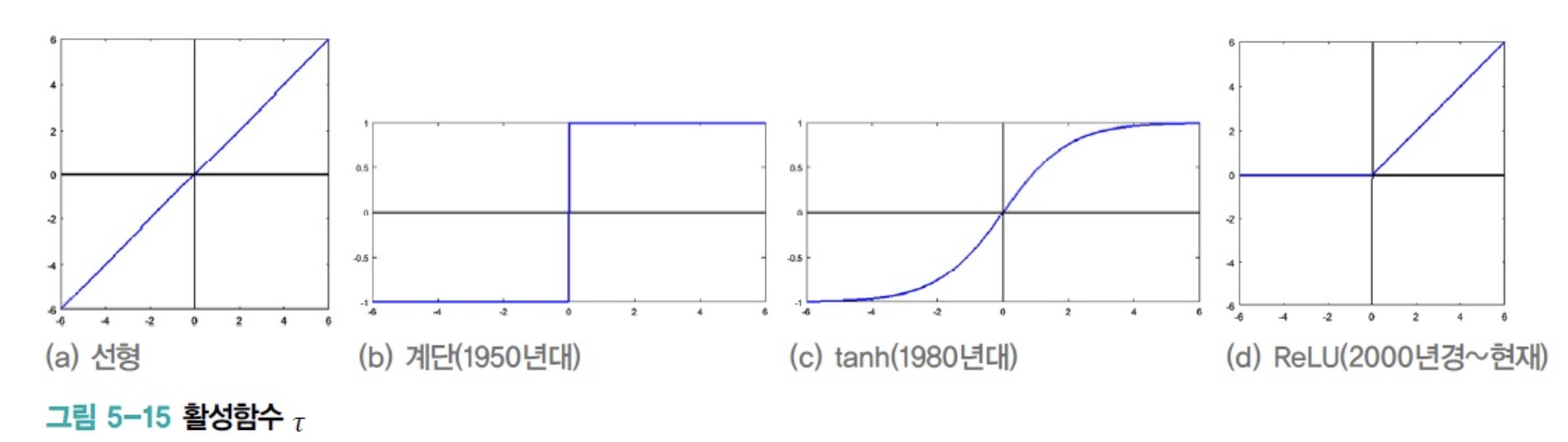
- MLP는 Perceptron에 Hidden Layer를 추가하고 tanh함수를 적용하여 획기적인 성능 향상을 얻었고 신경망을 부활시켰다.
  [0, 1] 범위를 갖는 Sigmoid도 활용되지만,
  [-1, 1] 범위를 갖는 tanh가 우월하여 주로 이를 활용한다.
- tanh는 전 구간에서 미분할 수 있는 장점이 있는데, 값이 어느 정도 커지면 1에 근접하는 saturation(포화)현상이 일어난다.
  이 함수의 변화량, 즉 미분값은 0에서 가장 크며 0에서 멀어질수록 작아지다가 포화 영역에 들어서면 0에 가깝다.
  
  예를 들어 $z=10$ 일 때 tanh(z)의 미분값은 0.000091이다.
  미분값이 0에 가까우면 매개변수 update가 매우 느리게 일어나 학습에 큰 지장을 준다.
  또한, 거의 모든 노드의 $y$ 가 0이 아니므로 신경망이 항상 매우 밀집된 상태가 된다.
  ➡️ 이러한 현상이 학습에 장애물이라는 사실을 깨닫게 되면서 새로운 Activation Function의 필요성을 느끼게 된다
- 1990년 말에 ReLU(Rectified Linear Unit) Activation Function이 제안된다.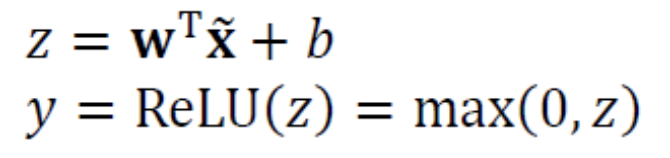ReLU는 양의 영역이 선형이므로 포화 현상이 발생하지 않는다.
  또한, 음의 영역은 0이 되므로 신경망을 희소하게 만드는 효과가 있다.
  
  예를 들어, 신경망이 임의로 초기화하여 약 반절 정도의 노드에서 $z$ 가 음수가 된다면,
  이 노드들은 모두 0을 가지게 되어 신경망은 희소한 상태가 된다.
  ➡️ 신경망이 희소(sparse)한 상태가 되면, 각 뉴런(neuron)이 입력 데이터에서 특정한 변화 인자(feature)를 담당하는 것이 더욱 명확해지는데,
  이는 서로 다른 변화 인자를 분리하고 독립적으로 학습할 수 있도록 도와준다.
  이를 통해, 신경망은 데이터에서 다양한 변화 인자들을 추출, 활용하여 복잡한 패턴을 학습하게 된다.
  
  ReLU는 0에서 미분이 불가능하다는 문제가 있다.
  하지만 기계 학습은 정확한 최저점을 찾는 대신 최저점에 가까운 점을 찾으면 되고,
  신경망의 분산구조로 인해 gradient가 수많은 경로로 흐르므로 한두 군데에서 미분 불가능한 현상을 문제거리가되지 않는다.
- ReLU를 변형한 함수에는 여러가지가 있으며,
  Leakey ReLU, PReLU(Parametric ReLU)가 대표적이다.
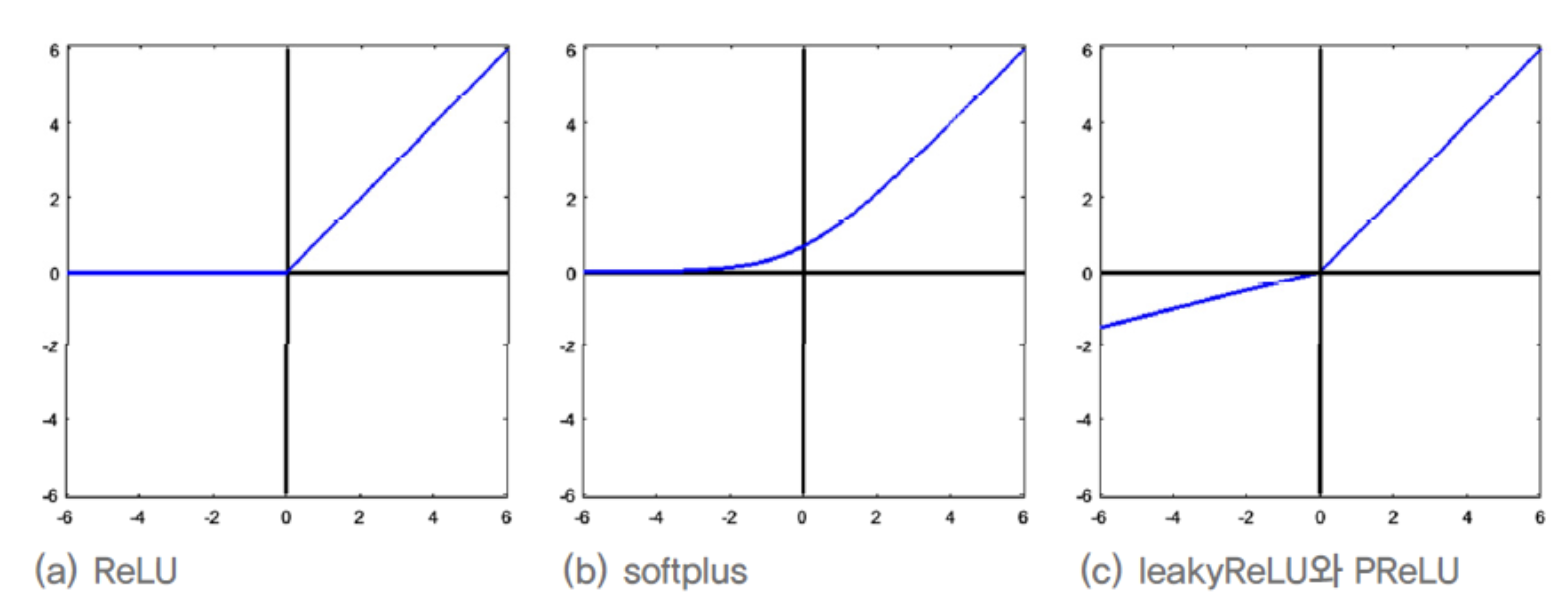
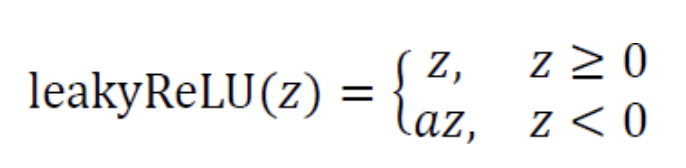
  - 모든 구간에서 미분 가능한 softplus함수와 성능을 비교한 결과,
    ReLU가 우월함을 확인.
  - $a < 1$ 이어야 하는데 보통 0.01을 사용한다. PReLU는 $a$ 를 학습으로 알아낸다.

Batch Normalization

Covariate Shift 현상

batch normalization을 사용하는 이유 : covariate shift 현상 극복
아래 그림은 학습 도중에 각 층에 입력되는 Training Set을 보여 준다.
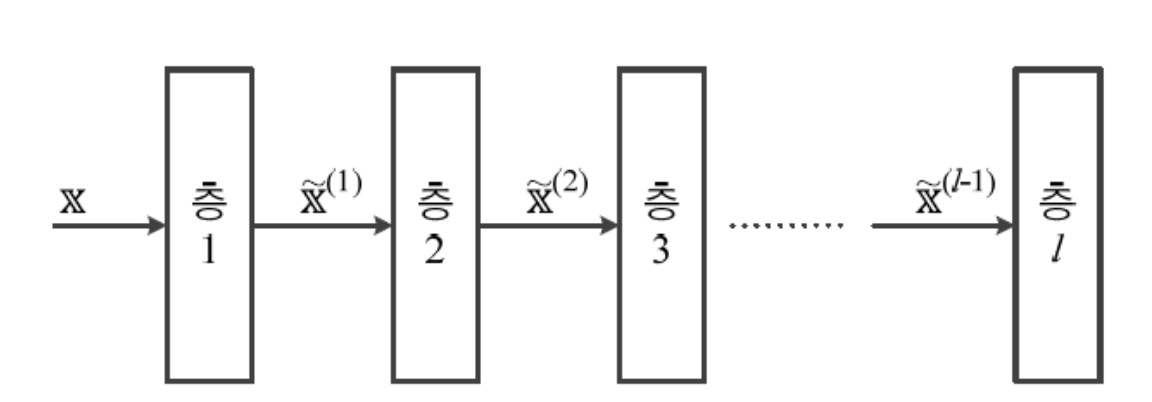
- 첫 번째 층, 즉 층 1에 원래 Training Set이 입력되는데,
  층 2는 층 1의 매개변수에 따라 변형된 Training Set $X^1$ 을 입력받는다.
- 그런데 학습 과정에서 층 1의 매개변수값이 계속 바뀌므로 $X^1$ 도 계속 따라 바뀐다.
  다시 말해, 층 1로 입력되는 sample의 분포는 일정한데 층 2로 입력되는 sample의 분포는 수시로 바뀐다.
  ➡️ 이처럼 학습 도중에 sample을 분포가 바뀌는 현상을 covariate shift라고 한다.
  covariate shift 현상은 층이 깊어질수록 심각해진다.
  즉 $X^2$ 는 $X^1$ 보다 분포가 더 심하게 변한다.
  ➡️ covariate shift는 깊은 구조의 신경망 학습이 잘 되지 않는 이유 중 하나로 꼽힌다.

Batch Normalzation 개념

Batch Normalization(배치 정규화)는 단순하면서도 매우 효과적이어서 최근 주목받는 기법이다.
앞서 공부했던 정규화를 위한 식은 학습을 시작하기 전,
Training Set $X$ 에 한 번 적용하면 됐다.
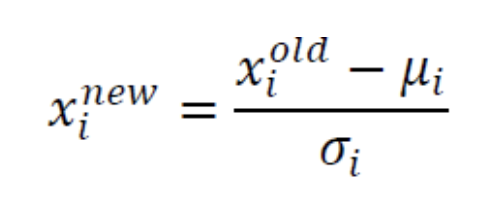
Batch Normalization은 위의 식을 모든 층에 독립적으로 적용하는 기법이라고 생각하면 된다.
- Batch Normaliztion은
  input $x$ 에 적용하는 것보다
  Activation Function에 입력하기 전 선형 연산을 거친 $z$ 에 적용하는 것이 좋다.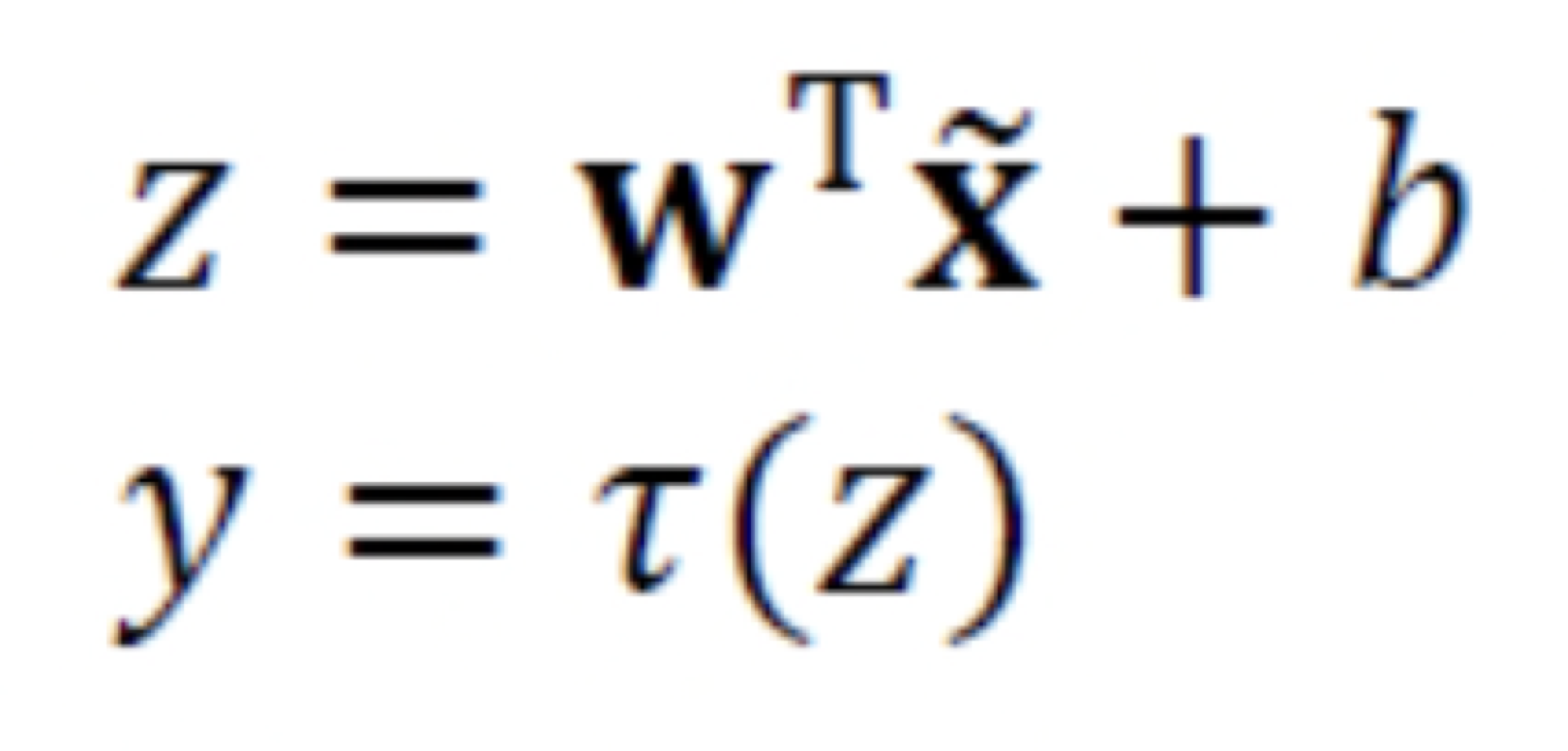
- 또한 Training Set 전체에 적용하는 것보다
  mini batch 단위로 적용하는 것이 우월하다는 사실이 확인되었고,
  이 때문에 Batch Normaliztion이라는 이름이 붙었다.
신경망의 각 node는 다음의 코드를 이용하여 정규화 변환을 수행한다.
- 현재 mini batch를 $X_B = {x_1, x_2, ..., x_m}$ 이라고 한다. (mini batch의 크기 : $m$ )
- 전방계산을 통해 $z$ 가 되었다고 하자. ( $z=w^Tx+b$ )
- 이러한 mini batch에 있는 sample 각각에 적용하여 $X_B={z_1, z_2,..., z_m}$ 을 얻었다고 가정.
- 이제 $X_B$ 를 갖고 코드 1을 수행한다.
  
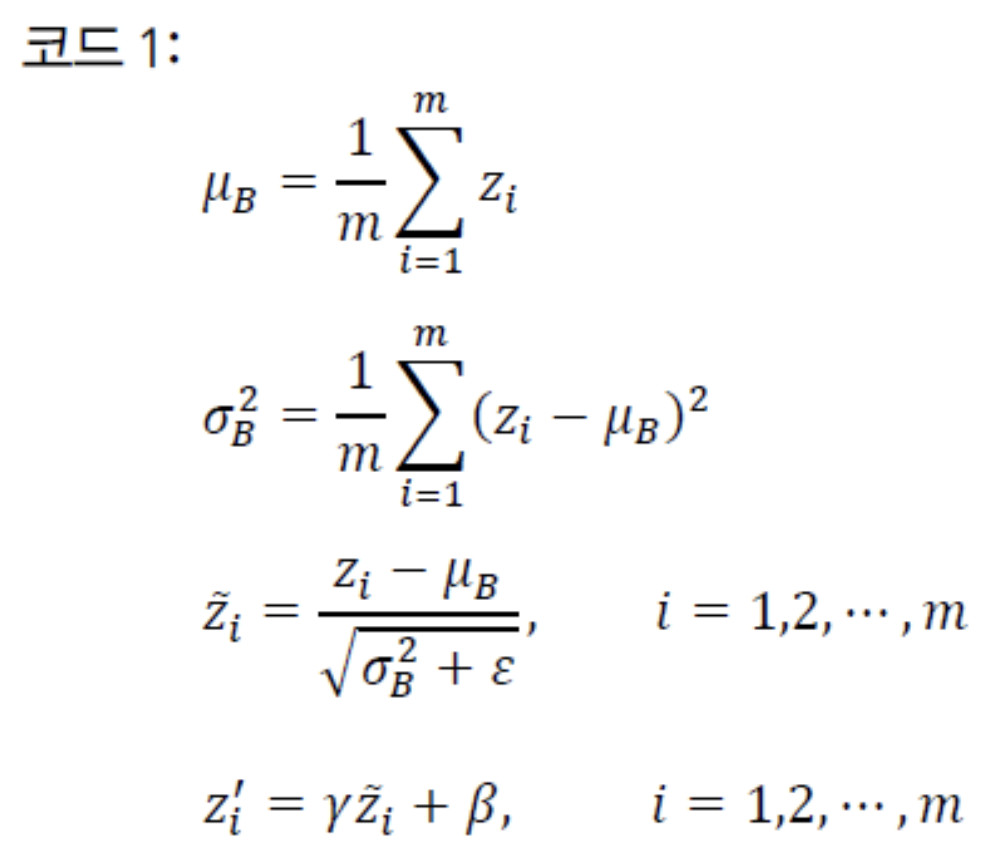
  ➡️ Batch Normalization에서는 mini batch 단위로 중간 결과를 모은 다음
  평균 $\mu_B$ 와 분산 $\sigma_B^2$ 을 구하고,
  평균과 분산을 이용하여 정규화 변환값 $\tilde{z}_i$ 를 구한다.
  
  ➡️ 그리고 $\gamma$ 와 $\beta$ 로 선형 변환을 수행하여 얻은 $z_i'$ 를 Activation Function에 입력한다.
  이처럼 $z_i$ 를 $z_i'$ 로 변환하는 일이 batch normalization의 핵심이다.
  ( $\gamma$ , $\beta$ 는 노드마다 고유한 매개변수로서 학습으로 알아내야 한다.)
SGD에 코드 1을 추가하여 Optimization을 마치면, 추가적인 후처리 작업이 필요하다.
코드 2는 이 작업을 수행하는데, 신경망의 각 node에 독립적으로 적용한다.
코드 1은 mini batch 단위로 처리했는데, 코드 2는 전체 Training Set을 가지고 처리한다.
- Training Set $X$ 를 전방계산을 통해 $\tilde{X}$ = { $z_1, z_2, ..., z_n$ }을 얻었다고 가정한다.
- 이제 $\tilde{X}$ 를 갖고 코드 2를 수행한다.
Batch Normaliztion을 CNN에 적용할 때 주의할 점이 있다.
CNN에서는 node 단위가 아니라 Feature Map 단위로 코드 1과 코드 2를 적용한다.
Feature Map 크기가 $p*q$ 라면 mini batch에 있는 sample마다 $pq$ 개의 값이 발생하므로
코드 1은 총 $pqm$ 개의 값을 가지고 $\mu_B$ 와 $\sigma_B^2$ 를 계산한다.
$\gamma$ 와 $\beta$ 는 Feature Map마다 하나씩 있다.

Batch Normaliztion 장점

매개변수 초기값에 덜 민감
Learning Rate를 크게 설정하여 수렴 속도 향상
Sigmoid를 Activation Function으로 사용하는 깊은 신경망도 학습이 이루어짐
규제 효과를 제공(dropout 규제를 적용하지 않고도 높은 성능)

규제의 필요성과 원리

Overfitting에 빠지는 이유와 피하는 전략

다음은 학습 model의 용량에 따라 Generalization 능력이 어떻게 변하는지를 개념적으로 보여준다.
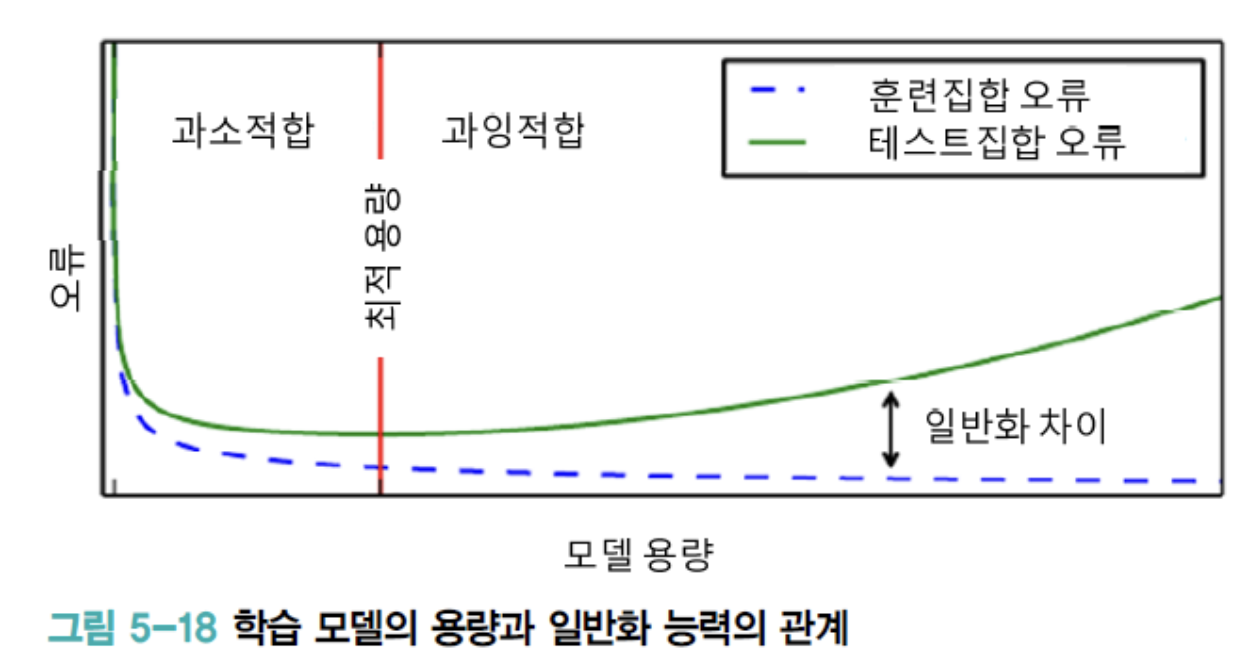
- Perceptron은 선형 model이라 용량이 매우 작은 편에 속하며,
  CNN은 용량이 매우 큰 편에 속한다.
- Training Set에 대한 오류율은 model의 용량이 클수록 0에 가까워진다.
  하지만 최적 용량을 지나면 Test Set에 대한 성능은 오히려 악화되어 Generalization 능력은 점점 떨어진다.
- 따라서 현대 기계 학습은 충분히 큰 용량의 신경망 구조를 설계한 다음,
  학습 과정에서 여러 가지 규제 기법을 적용하는 전략을 구사한다.

규제의 정의

주어진 data를 근사화하는 함수를 구하거나 주어진 data로 방정식을 푸는 등의 문제에서
model 용량에 비해 data가 부족한 경우는 불량 문제(ill-posed problem)이 된다.
이러한 ill-posed problem을 풀기 위해서 적절한 가정을 투입할 수 밖에 없다.
티호노프는 이 해결책으로 규제를 최초 제안한 사람 중 한 명이다.
그는 문제의 성질 중 가장 보편적인 "입력과 출력 사이의 mapping은 매끄럽다"라는 성질을 사용하였다.
➡️ 이처럼 data의 원천에 내재한 정보를 사전 지식(prior knowledge)이라고 한다.
다음의 그림은 "입력과 출력 사이의 mapping은 매끄럽다"는 성질을 직관적으로 설명한다.
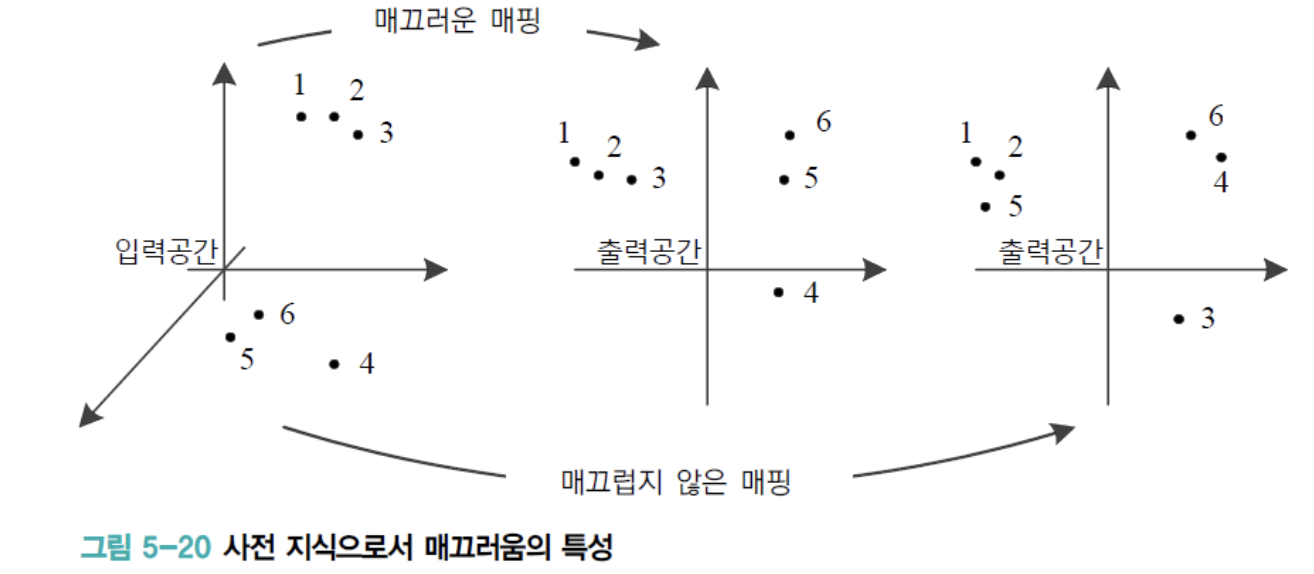
- 맨 왼쪽은 입력 data 공간이고,
  가운데와 오른쪽은 다른 두 가지 함수로 mapping된 출력 공간이다.
- 가운데 mapping을 살펴보면, 입력 공간에서 서로 거리가 가까운 sample은
  출력 공간에서도 가깝다는 사실을 알 수 있다.
  따라서 매끄러운 함수(smooth function)라 할 수 있다.
- 반면 오른쪽 mapping에서는 입력 공간에서 서로 가까운 sample이 출력 공간에서 먼 경우가 있다.
  따라서 매끄럽지 않은 함수이다.
타호노프의 규제 기법은 이러한 매끄러움 가정에서 다음의 식을 사용하여 학습한다.
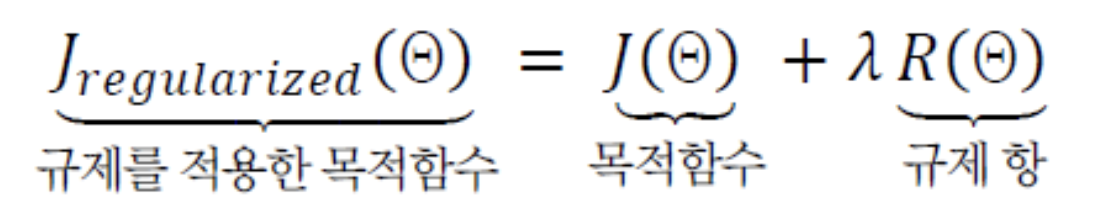
- 학습 알고리즘은 원래 목적함수 $J(\Theta)$ 에 규제 항을 더한 목적함수를 사용한다.
- 규제 항은 해 $\Theta$ 의 매끄러운 정도를 나타내는데, 덜 매끄러울수록 큰 값을 부여하여 벌칙을 강화한다.
  ➡️ 매끄러움 성질은 현대 기계학습에서도 유용하게 사용된다.
  거의 기본으로 적용되는 가중치 감쇠(weight decay)는 위의 식과 비슷한 원리를 사용한다.
  또한, Chap 06에서 공부할 Unsupervised Learning 알고리즘 대부분도 매끄러움 가정에서 개발되었다.
딥러닝은 규제기법으로 인해 실용화에 안착했다고 말해도 될 정도로
아주 효과적인 규제 기법이 다양하게 개발되었다.

규제 기법

Weight Penalty

목적함수 $J$ 와 $J_{regularized}$ 는 가중치집합 $\Theta$ 와 Training Set $X, Y$ 에 영향을 받지만,
규제 항 $R$ 은 Training Set과 무관하다.
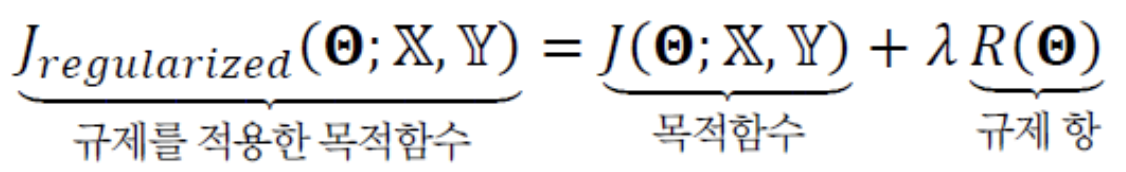
- $R$ 은 단지 weight의 크기에 제약을 가하는 역할만 한다.
  다시 말해, data set과 무관하게 원래 있는 사전 지식으로 해석할 수 있다.
- 매개변수 $\Theta$ 는 weight와 bias로 구성된다.
  하지만 위의 식은 보통 weight에만 적용하고, bias에는 적용하지 않는다.
  다시 말해, weight는 $J_{regularized}$ 를 사용하고 bias는 원래 목적 함수인 $J$ 를 사용한다.
  ➡️ weight는 node 사이의 상호작용을 표현하기 때문에 규제가 필요하지만,
  bias는 하나의 node에만 관련되어 규제를 하지 않아도 문제될 것이 없기 때문이다.
  따라서 지금부터 $\Theta$ 는 bias를 빼고 weight만 포함한다.
- 또 위의 식은 모든 층이 같은 계수 $\lambda$ 를 사용한다.
  하지만 은닉층마다 자신에 적합한 계수를 사용하도록 확장할 수 있지만,
  이 책에서는 모든 은닉층이 같은 계수를 사용한다고 가정한다.

1. L2-norm (weight decay)

규제 항 $R$ 로 가장 널리 쓰이는 것은 L2-norm이며,
L2-norm을 사용하는 규제 기법을 weight decay기법이라고 한다.
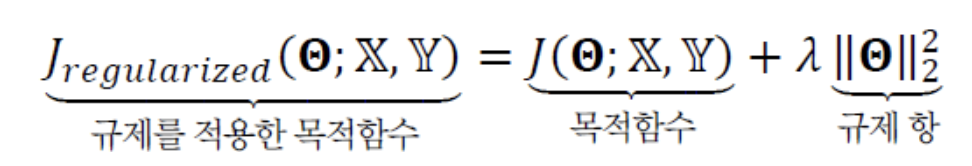
- 규제 항 R은 L2-norm의 제곱이다.
- 만약 Linear Regression을 푸는 경우라면, Ridge Regression이라고 한다. (곧 이어 다룰 내용)
- 목적함수가 달라졌으므로, 학습 알고리즘이 사용하는 gradient 식도 바뀌어야 한다.
위의 식을 미분하면(= gradient를 구하면) 다음의 식이 된다.
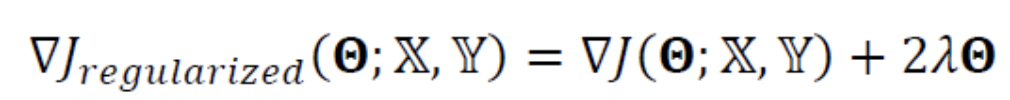
gradient를 이용하여 매개변수를 update하는 식을 다음과 같이 유도할 수 있다
- $\lambda = 0$ 으로 설정하면, 규제를 적용하지 않은 원래 식, $\Theta$ = $\Theta - \rho \Delta J$ 가 된다.
- 원래 식과 규제를 적용한 식을 비교하면,
  원래 식의 $\Theta$ 에 (1- $2 \rho \lambda$ )를 곱한 것뿐이다.
- $\lambda$ 는 L2-norm 계수이고, Learning Rate인 $\rho$ 는 1보다 훨씬 작은 수를 사용하므로
  $2 \rho \lambda$ 는 1보다 작은 수가 된다.
- 따라서 $2 \rho \lambda$ 만큼 매개변수를 축소한 다음 $- \rho \Delta J$ 를 더하는 효과를 준다.
  이러한 과정을 반복하여 적용하므로, 결국 최종해를 원점 가까이 당기는 효과를 준다.
  (가중치를 작게 유지하는 효과)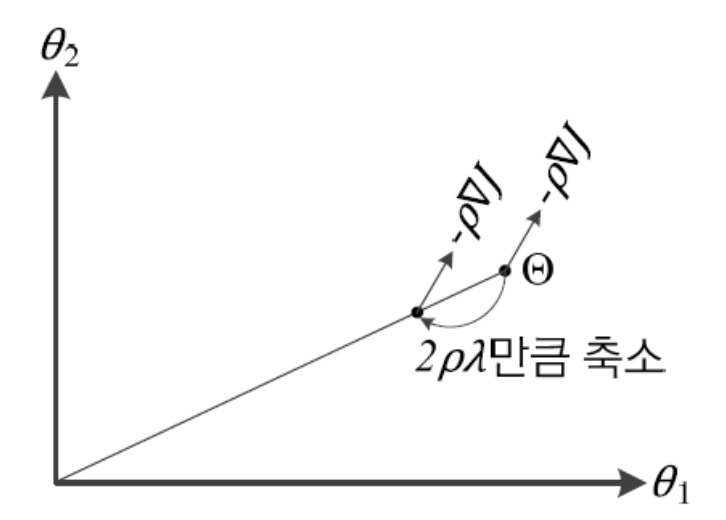

Ridge Regression

Weight Decay(규제 항으로 L2-norm을 사용하는 규제)를 Linear Regression에 적용해보자.
Training Set을 다음과 같이 정의
$X =$ { $x_1, x_2, ..., x_n$ }, $Y =$ { $y_1, y_2, ..., y_n$ }
$w=$ { $w_0, w_1, ..., w_d$ } $^T$ 는 hyper plane을 표현하는 매개변수이다.
bias $w_0$ 은 0이라고 가정한다.
다시 말해, hyper plane이 원점을 지난다고 가정한다.
➡️ 행렬로 표시하면 다음과 같다
$Xw = y$
Weight Decay를 적용한 목적함수는 다음과 같이 정의할 수 있다.
다음의 목적함수를 풀어 최적의 매개변수값을 구하는 문제를 Linear Regression이라고 한다.
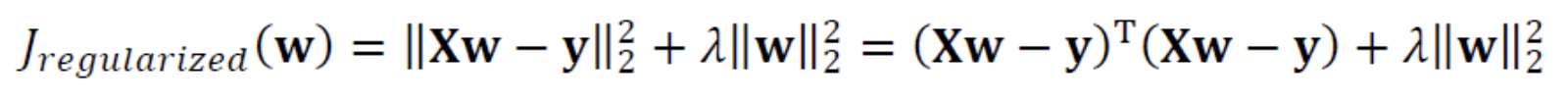
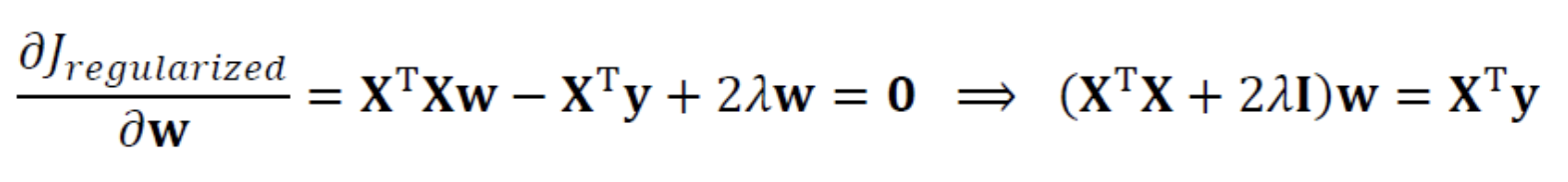
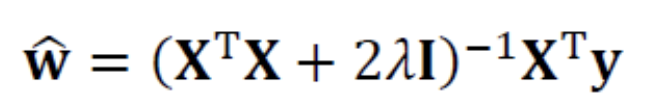➡️ 공분산 행렬 $X^TX$ 의 main diagonal이 2 $\lambda$ 만큼 증가.
역행렬을 곱하므로 weight를 축소하여 원점으로 당기는 효과
예측 단계에서는 위에서 구한 최적의 매개변수값을 사용한다.
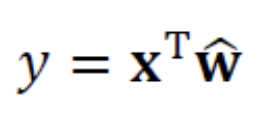
규제항에 L2-norm을 적용한, 즉 Weight Decay를 적용한 Linear Regression을
Ridge Regression이라고 한다.
Ridge Regression의 예시를 살펴보자.

MLP와 DMLP에 적용

규제항에 L2-norm, 즉 Weight Decay를 DMLP에 적용하면 다음과 같다

2. L1-norm

L1-norm을 적용한 식은 다음과 같다.
L1-norm : 개별 요소의 절댓값을 모두 더한 값.
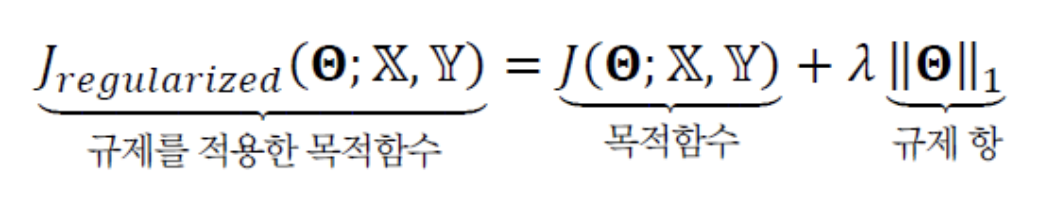
위의 식을 미분하면 다음과 같이 된다.
( $sign(\Theta)$ 는 $\theta_1, \theta_2, ...$ 의 부호로 구성되는 vector로서,
vector의 요소가 양수면 1, 음수면 -1을 가진다.)
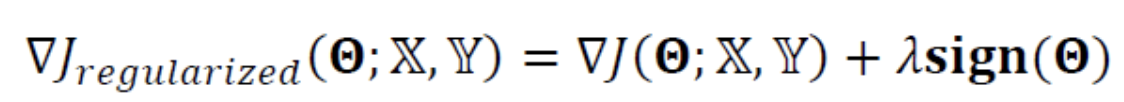
위 식의 gradient를 이용하여 매개변수를 update하는 식을 유도하면 다음과 같다.
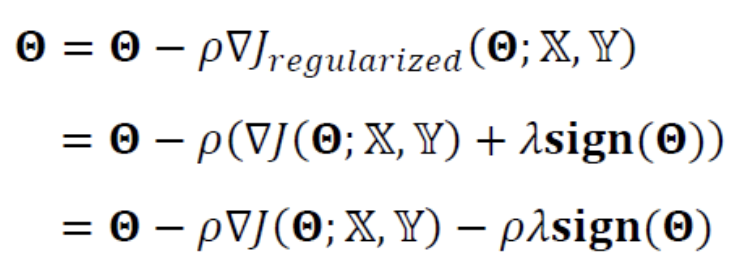
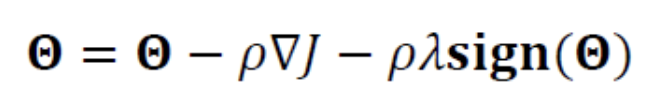
다음은 L1-norm을 이용한 weight penalty 효과를 보여준다
(a) : $sign(\theta) = (1, 1)^T$ 이기 때문에 $(-\rho\lambda, -\rho\lambda)^T$ 만큼 추가로 이동한다.
(b) : $sign(\theta) = (-1, 1)^T$ 이기 때문에 $(\rho\lambda, -\rho\lambda)^T$ 만큼 추가로 이동한다.
➡️ L1-norm은 해를 원점 방향으로 당기는 효과가 있다는 사실을 알 수 있다.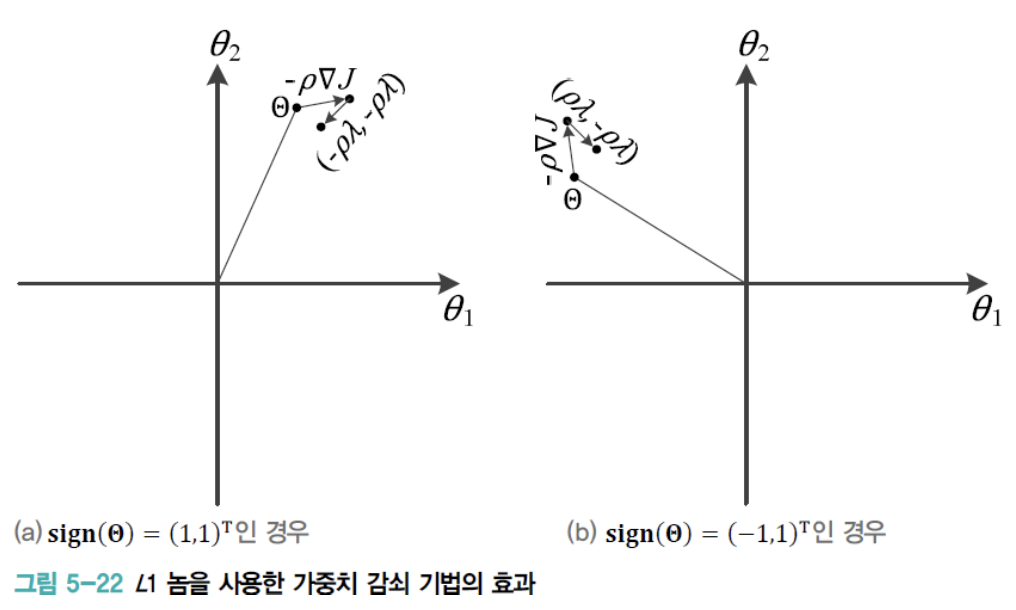
여러 문헌에서 L1-norm을 사용하면 0이 되는 매개변수가 많다는 현상이 입증되었으며,
이 현상을 희소성(saprsity)이라고 한다.
만약 L1-norm을 Linear Regression에 적용하면 0이 아닌 항만 남으므로
L1-norm이 특징 선택을 한다고 표현한다.
신경망에 적용하는 때에는 0이 된 weight를 제거함으로써
Full-Connected 구조를 Sparsely-Connected 구조로 바꿀 수 있다.

Lasso Regression

규제 항으로 L1-norm을 사용하는 규제를 Lasso Regression이라고 한다.

Early Stopping

아래 그림의 가로축을 시간, 즉 epoch 수로 바꾼 그래프이다.
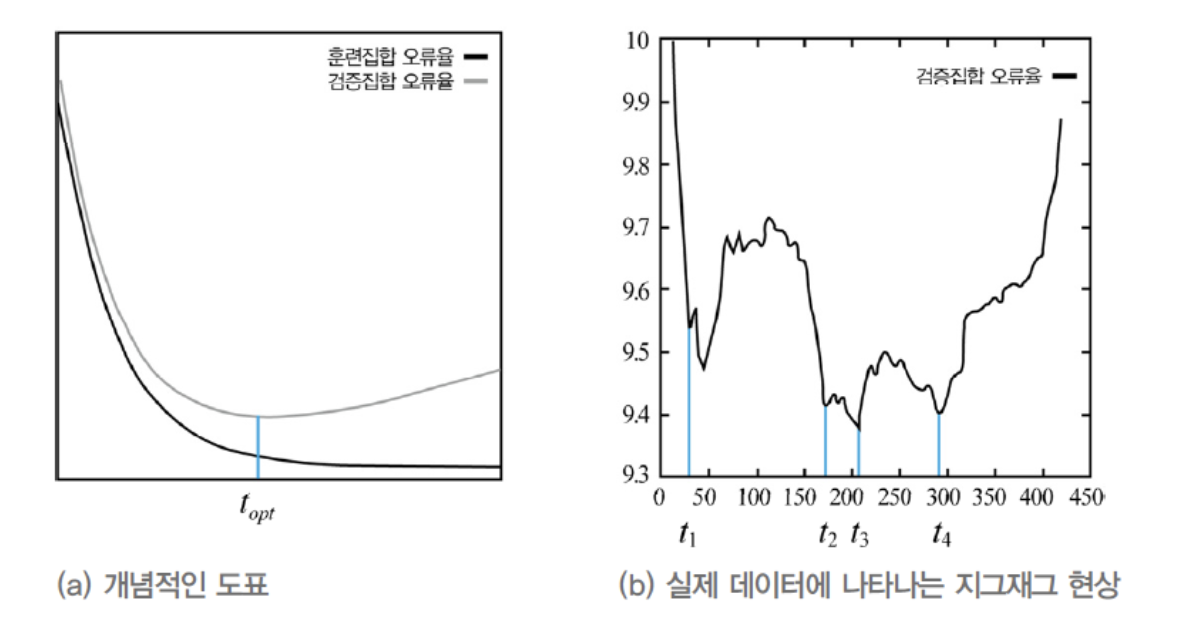
- 학습을 오래 시킬수록 더 최적점에 접근한다.
- 하지만 어떤 지점을 넘어서면 Train Set을 '암기'하기 시작하여,
  Validation Set에 대해서는 성능이 점점 떨어지기 시작한다.
  다시 말해, Generalization 능력이 떨어지기 시작한다.
따라서 Genralization 능력이 최고인 지점,
즉 Validation Set의 오류가 최저인 지점을 만나면 그곳에서 멈추는 전략이 매우 효과적이다.
이 전략은 조기 멈춤(early stopping)이라고 한다.
다음은 과감한 early stopping 알고리즘이다 (좋지 않은 알고리즘)
- 실제 세계에서 위의 알고리즘은 이상에 불과하다.
- 아래와 같은 Test Set에 대해서는 $t_1$ epoch일 때 멈춘다.
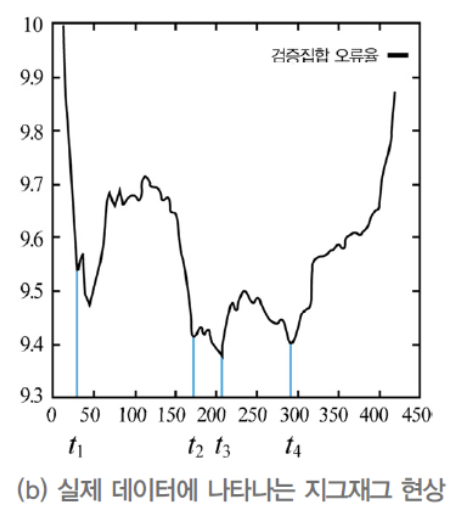
- 한마디로 너무 과감한 early stopping이 된다.
이러한 문제를 다루는 방법이 여러 가지 있는데,
가장 단순한 방법은 $t$ 이후에 연속으로 $p$ 번 동안 성능 향상이 없으면 멈추는 것이다.

예를 들어, $p=3$ 으로 설정된 상황에서,
$t = [50, 51, 52, 53, 54, 55]$ 5epoch에 걸쳐
$오류율 = [0.23, 0.21, 0.24, 0.23, 0.27]$ 이 발생했다면
$t=51$ 에서 멈추기로 하고 이 순간의 $\Theta$ 를 최적 매개변수로 취한다.
또는 이후 $p$ 세대 동안 연속으로 성능 저하가 있어야 한다는 좀 더 강한 조건을 사용한다.
이 경우에는 52 epoch보다 53 epoch에서 더 좋은 성능이 발생했으므로 멈추지 않고 계속 진행한다.

이 방식은 $p$ epoch만큼 참을성을 가지고 지켜보는 셈이므로
$p$ 를 참을성 인자라고 할 수 있다.
- epoch마다 조사하였는데, $q$ epoch마다 조사하는 방식으로 수정할 수 있다.
  다음은 참을성 인자로 $p$ , $q$ epoch마다 조사하는 방식의 코드이다.
- 만약 $p$ 와 $q$ 를 모두 1로 설정한다면, 과감한 조기 멈춤 알고리즘과 같아진다.
  반면, $p$ 를 너무 크게 설정하면 쓸데없이 계산 시간을 낭비하여 조기 멈춤의 효과가 없어진다.

참을성 인자 $p$ 를 사용한 알고리즘을 이용하여 최적의 멈춤 시기를 알아낸 다음에는
그 순간의 매개변수값을 그대로 사용할 수 있지만,
Train Set과 Validation Set을 합한 더 큰 Train Set을 만들어
처음부터 새로 학습할 수도 있다.
이때 매개변수값을 초기화하고 처음부터 새로 학습할 수도 있고,
최적 매개변수값 $\hat \Theta$ 에서 출발하여 추가로 학습하는 두 가지 방식이 있다.
두 가지 방식은 실험을 통해 선택하는 수밖에 없다.

Data Augmentation

Overfitting을 방지하는 가장 확실한 방법은 충분히 큰 Train Set을 사용하는 것이다.
하지만 현실적으로 데이터를 늘리는 일은 불가능하거나 어렵다.
또한 Train Set을 아무리 모아도 방대한 Feature Space에 비하면 매우 작다.
비용을 적게 들이며 data양을 늘리는 한 가지 방안은 현재 가진 data를 인위적으로 변형하는 것이다.
따라서 데이터 확대(Data Augmentation)는 잠재적인 변형을 program으로 구현하여 Sample 수를 강제로 늘리는 기법이라 정의할 수 있다.
예를 들어, data가 영상이라면 영상에 있는 물체에 이동, 회전, 또는 크기 변환을 가하면 된다.
이들은 모두 선형 변환으로서, affine transformation이라고도 한다.
주의할 점은 변형 정도가 너무 커서 다른 부류로 바뀌는 상황을 배제하는 것이다.
예를 들어, '6'을 180 $\degree$ 회전하면 '9'라는 다른 부류가 되므로
변형 정도를 상황에 따라 잘 조절해야 한다.
➡️ 이러한 방식은 사람이 data를 잘 살펴본 다음 적합한 변형을 설계해야 한다.
이러한 접근방법은 일종의 수작업 특징(hand-crafted feature) 설계라 할 수 있다.
MNIST data set에서 모든 부류가 똑같은 변형 방법을 사용한다면,
0이나 8은 6이나 9 때문에 변형에 제한을 받게 된다.
➡️ 하우버그는 이러한 한계를 극복하기 위해, 같은 부류에 속하는 Sample 2개 사이의 morphing 변환을 자동으로 알아낸 다음, morhping을 통해 더 자연스럽게 새로운 data를 생성하는 방법을 제안하였다.
맨 왼쪽 Sample을 가운데 Sample로 morphing하는 예를 보여 준다.
오른쪽 Sample은 morphing 변환과 morphing으로 얻은 새로운 Sample을 보여준다.
morphing은 비선형 변환으로서 affine transformation보다 훨씬 다양한 data를 생성할 수 있다.
이 방법은 morphing 변환을 자동으로 알아내므로
데이터 확대를 위한 비선형 변환 규칙을 학습한다고 말할 수 있다.
이제 숫자처럼 물체가 분리된 상황을 넘어, 여러 물체가 어지러운 배경에 섞여 있는 자연영상의 개수를 확대하는 일을 생각해보자.
ILSVRC 2012년도 대회에서 우승하여 딥러닝의 가능성을 펼친 논문 [Krizhevsky2012]가 자연영상을 확대하는 데 사용한 방법을 소개한다.
➡️ 이 논문은 Data를 확대하기 위해 두 가지 기법을 사용하였다.
1. 첫 번째 기법에서는
  $256 * 256$ 크기의 입력영상에서 임의로 위치를 다르게 하면서
  $224 * 224$ 영상을 1,024장을 잘라 이동 변환 효과를 거두었으며,
  좌우 반전까지 시도하여 2,048배만큼 확대하였다.
  
  예측 단계에서는 입력영상을 입력영상을 네 구석과 중앙점을 중심으로
  5장의 $224 * 224$ 영상으로 잘라내고(Cropping) 각각에 좌우반전(Mirroring)을 시도하여 10장의 영상을 만든 다음, 10장의 예측 결과를 평균하여 최종 인식한다.
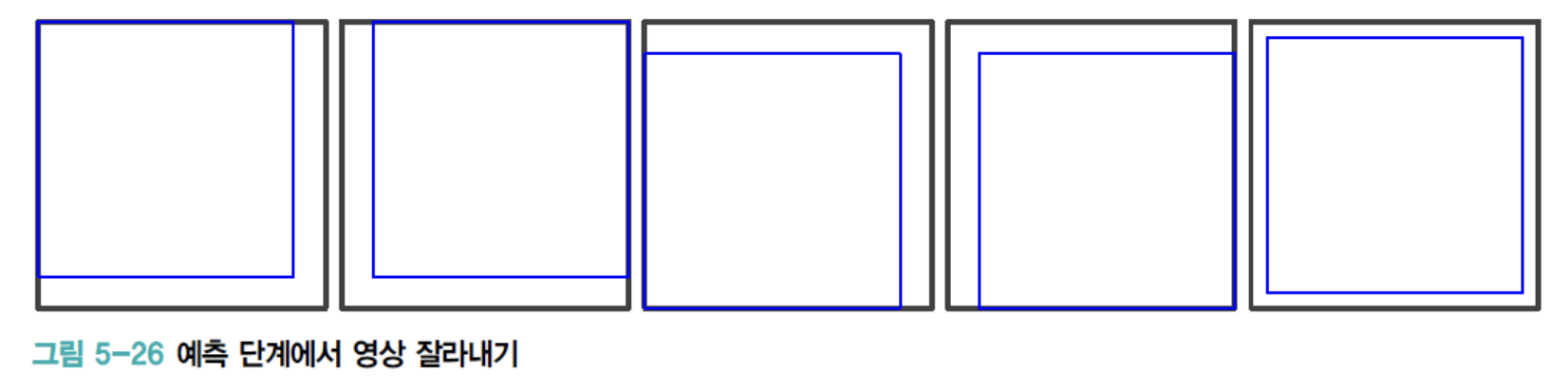
2. 두 번째 기법에서는
  색상을 변형한다.
  영상을 구성하는 화소를 RGB 3개 값으로 구성된 3차원 Sample로 간주한다.
  이렇게 만든 Sample Set에 PCA 변환을 적용한 다음,
  PCA로 구한 eigen vector와 eigen value 정보를 이용하여 색상에 변환
  (PCA color augmentation)을 가한다.
  
  또한 입력에 noise를 섞는 기법(noise addition)도 데이터 확대의 하나이다.
  예를 들어, 원래 Sample이 (0.112, 0.320, 0.670) $^T$ 였다면,
  Gaussian Distribution에서 생성된 임의 noise (0.003, -0.010, 0.013) $^T$ 을 더해
  (0.115, 0.310, 0.683) $^T$ 를 입력하는 것이다.
  더 나아가 은닉 노드에도 noise를 섞어 성능을 향상하기도 한다.

dropout

dropout 기법은 매우 단순하지만, 규제 효과가 매우 강력하여 현대 기계학습에서 널리 사용된다.
dropout이란, 입력층과 은닉층의 노드 중 일정 비율로 임의로 선택하여 제거하는 작업이다.
선택된 node는 자신에게 들어오는 edge와 나가는 edge까지 모두 제거한다.
제거하고 남은 부분 신경망으로 학습을 진행한다.
➡️ 따라서 서로 다른 부분 신경망을 아주 많이 만드는 셈이다.
➡️ Sample 하나가 학습에 여러 번 참여하므로 Sample의 개수보다 훨씬 많은 부분 신경망이 만들어진다.
Train Set에 있는 Sample 개수가 $n$ 이고
한 Sample이 평균 $k$ 번 학습에 참여한다면,
$nk$ 개의 부분 신경망이 만들어진다.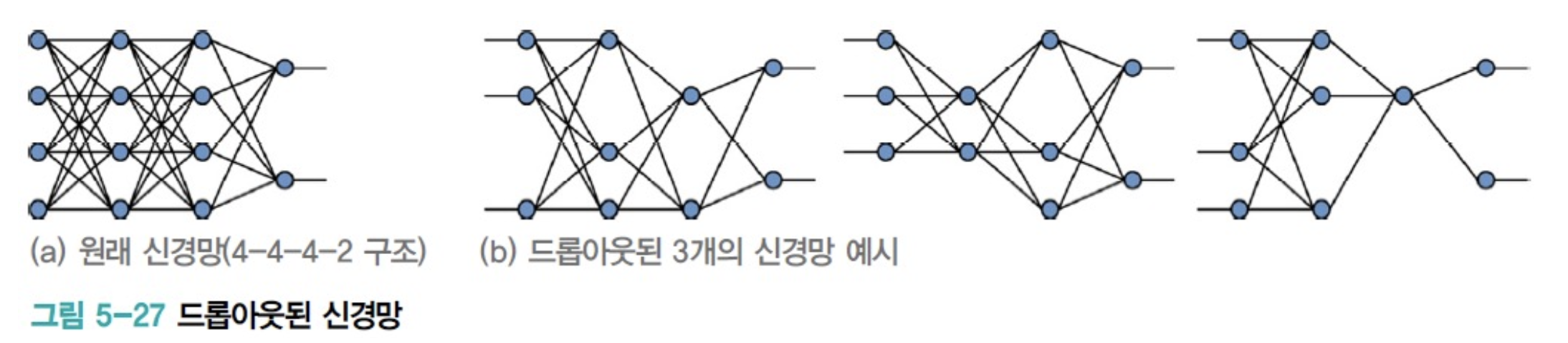
예측 단계에서는 입력 Test Sample을 학습에서 사용했던 모든 부분 신경망에 입력하여 예측 결과를 받은 다음,
투표를 통해 최종 결과를 결정하면 된다.
이처럼 여러 개의 예측기를 결합하는 접근방식을 앙상블 기법이라고 하며,
dropout을 앙상블의 일종으로 볼 수 있다.
(앙상블 기법은 Chap 12에서..)
하지만 부분 신경망이 독립적으로 동작하는 방식으로 앙상블 기법을 적용하는 데에
장애물이 있다.
dropout된 부분 신경망마다 적절한 hyper parameter를 설정하고 학습시키는 일은
힘든 작업일 뿐만 아니라, 학습된 부분 신경망을 저장하는 데에 메모리가 많이 필요.
또한 예측 단계에서 많은 시간 소요 ➡️ 실시간 동작이 필수인 응용에서는 심각한 문제
본격적으로 dropout 기법을 설계하자.
➡️ 아래의 알고리즘은 mini batch를 사용하는 version에 dropout을 적용하는데,
다른 version에도 유사하게 적용하면 된다.
- $\pi$ : boolean 배열.
- $\pi^l$ : l번째 층의 node 제거 여부를 나타내는 vector
  (제거된 node = 0, 살아남은 node = 1)
- $L$ 번째 층은 output layer이므로 dropout 대상이 아니며, $\pi^L$ 은 없다.
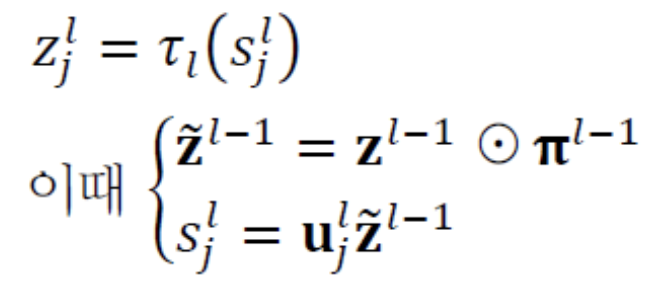  ➡️ Line 6 : 전방 계산을 수행한다. dropout을 적용한 전방계산 식은 다음과 같다. $\pi$ 는 Sample마다 독립적으로 정하는데, 난수를 이용하여 설정한다.
  이때 0이 될, 즉 제거될 비율을 지키는 것이 중요하다.
  보통 input layer에서 제거될 비율은 $p_{input} = 0.2$ ,
  hidden layer에서 제거될 비율은 $p_{hidden} = 0.5$
  로 설정하면 적절하다고 보고되어 있다.
  (즉, input layer는 10개 중 2개 제거하고, hidden layer는 10개 중 5개 제거)
  
  ➡️ Line 7 :
  Error backpropagation을 이용하여 부분 신경망의 gradient ( $\Delta_i^{dropout}$ )을 계산한다.
  이때 $\pi$ 를 보면 가중치의 제거 여부를 쉽게 알 수 있는데,
  제거된 가중치만 빼고 원래 Error backpropagation을 그대로 적용하면 된다.
  
  ➡️ Line 8 : mini batch에 속한 모든 Sample의 gradient 평균을 계산한다.
  이때 가중치마다 살아남은 횟수가 다르므로,
  가중치별로 횟수를 세어 평균을 구한다.
  
  ➡️ Line 9 : 평균 gradient를 이용하여 가중치를 갱신한다.
  
  ➡️ 예측 단계 : 학습이 끝나고 예측 단계에서 주목할 점은
  서로 다른 신경망을 명시적으로 여러 개 만들어 따로따로 저장한 것이 아니라,
  weight sharing 기법을 통해 단 하나의 신경망을 만들었다는 사실이다.
  아래의 그림과 같이 단 하나의 신경망으로 앙상블 효과를 거두어야 한다.
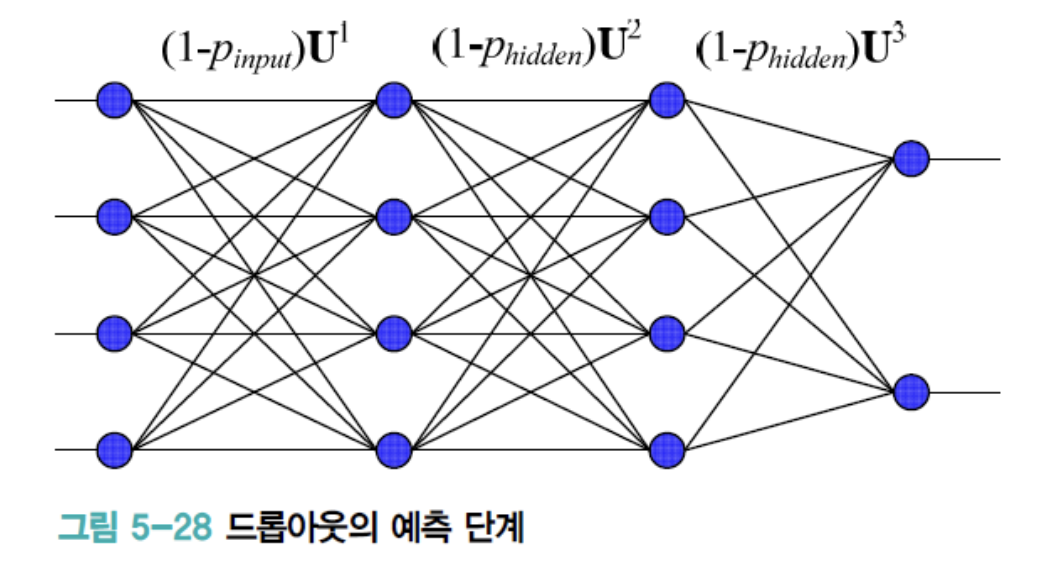  새로운 Sample이 입력되면, dropout을 사용하지 않는 보통 신경망처럼
  전방 계산을 하여 예측하는데,
  단지 가중치에 생존 비율, 즉 $(1 - dropout비율)$ 을 곱하여
  가중치의 규모를 줄인 다음에 전방 계산을 한다.
  input node에서 나가는 weight에는 $(1-P_{input})$ 을 곱하고,
  hidden node에서 나가는 weight는 $(1-P_{hidden})$ 을 곱한다.
  
  이렇게 규모를 줄이는 이유는 학습 과정에서 weight는 $(1-dropout비율)$ 만큼만 참여했기 때문이다.
  
  memory는 boolean 배열 $\pi$ 만 추가로 필요하다는 장점이 있다.
  하지만 부담은 신경망의 크기에서 온다.
  dropout된 비율만큼의 node가 쉬므로 dropout을 채택하지 않는 신경망에 비해
  hidden layer 수를 $\frac{1}{P_{hidden}}$ 만큼 늘리도록 권고.
  예를 들어, $P_{hidden} = 0.5$ 라면 hidden node 수를 2배로 늘리면 된다.

앙상블 기법

서로 다른 여러 개의 model이 예측한 결과를 결합하면 Generalization 오류를 줄일 수 있다.
이처럼 model을 결합 하는 기법을 앙상블(ensemble) 기법이라 하며,
현대 기계학습에서는 emsemble기법도 규제 기법의 하나로 여긴다.
Esemble 기법에서 서로 다른 model을 결합하는 여러가지 방식이 있다.

model averaging : 여러 model의 출력으로부터 평균을 구하거나 투표하여 최종 결과를 결정
bagging(bootstrap aggregating) :
Train Set $X$ 를 sampling하여
$k$ 개의 서로 다른 새로운 Train Set $X_i', i = 1, 2,..., k$ 를 구축한다.
$X_i'$ 은 $X$ 에서 대치를 허용하여 임의로 $|X|$ 개의 Sample을 sampling하므로,
$X_i'$ 와 $X$ 는 크기가 같다.
대치를 허용했으므로 $X_i'$ 에는 같은 Sample이 여러 개 들어 있을 수 있다.

똑같은 신경망 model을 $k$ 개의 서로 다른 Train Set $X_i'$ 로 학습시켜
서로 다른 $k$ 개의 신경망을 만든다. ( $k$ 개의 신경망이 가급적 서로 독립이 되도록 유지한다.)
예측 단계에서는 투표로 최종 예측 결과를 결정하면 된다.
boosting :
$i$ 번째 만든 예측기가 틀린 sample을
$i+1$ 번째 예측기가 잘 인식할 수 있는 방식의 연계성을 가지도록 Ensemble을 구축한다.

Ensemble에 대한 자세한 내용은 Chap 12에서..

Hyper Prameter 최적화

기계학습에는 두 종류의 Parameter가 있다.

학습 알고리즘이 최적해야 하는 model 내부 parameter (weight)
model의 외부에서 model의 동작을 조정하는 Hyper Parameter
(Hidden Layer 개수, CNN mask 크기, stride, Activation Function, Learning Rate, momentum 등)

Hyper Parameter는 학습을 시작하기 전에 미리 설정해야 하는데,
적절한 값을 선택하는 것이 매우 중요하다.

Grid Search & Random Search

Hyper Parameter 조합을 생성하는 Line 3을 어떻게 구현하느냐에 따라
세 가지 방식 수동 탐색, 격자 탐색(Grid Search), 임의 탐색(Random Search)
으로 구분한다.
설정해야 할 Hyper Parameter가 2~3개인 경우에는 수동으로 처리할 수 있지만,
그 이상이면 너무 힘든 작업이다.
따라서 격자 탐색(Grid Search)이나 임의 탐색(Random Search)과 같은 자동 방식을 사용한다.
아래의 그림은 $h_1$ , $h_2$ 라는 2개의 Hyper Parameter가 있는 상황이다.
예를 들어,
$h_1$ 은 Learning Rate, $h_2$ 은 mini batch 크기
라고 생각할 수 있다.
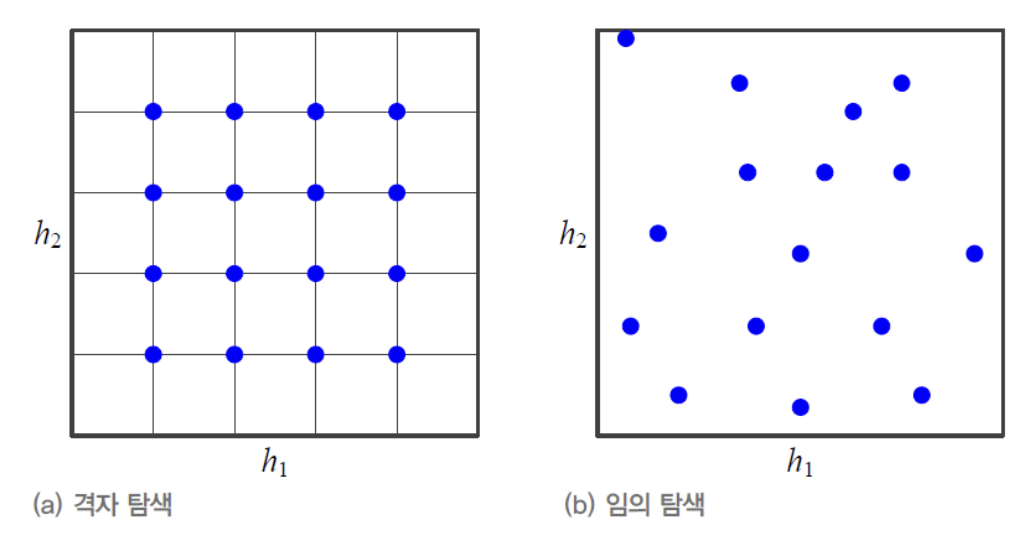
- Grid Search는 각각의 paramter를 일정한 간격으로 나눈 다음,
  교차점에 해당하는 값을 사용한다.
  다시 말해, 위의 알고리즘 Line 3은
  (a)의 파란 점을 순서대로 하나씩 parameter 조합으로 생성한다.
- Random Search는 난수를 이용하여 parameter 조합을 생성한다.
  이때 각각의 parameter 범위와 간격을 설정해야 한다.
  범위는 수동으로 설정해야 하는데,
  문헌이 제시하는 기본값을 중심으로 적절한 범위를 설정한다.
  
  간격을 설정할 때 중의할 점이 있는데, parameter에 따라 log 규모를 사용해야 한다.
  예를 들어,
  Learning Rate $\rho$ 의 범위를 0.0001 ~ 0.1로 설정하고
  등간격 0.001을 사용한다면, 0.001 ~ 0.1로 총 1,000개 값을 조사해야 한다.
  0.1처럼 큰 값에서는 굳이 0.0001 간격을 사용하여 세밀하게 조사할 필요가 없다.
  이러한 경우에는 log 규모를 사용하면 적당하다.
  
  즉, 2배씩 증가하면서 0.0001, 0.0002, 0.0004, 0.0008, ... 0.0256, 0.0512, 0.1024와 같은 값을 조사한다.
  이처럼 log 규모의 값을 사용하는 방식은 Grid Search나 Random Search 모두 적용된다
알고리즘 5-9로 찾은 최적값이 경계 부근에 위치한다면 건너편에 더 좋은 값이 있을 수 있다.
예를 들어, (b)에서 맨 오른쪽 점이 $h_1$ 최적점으로 선택되었다면,
$h_1$ 은 오른쪽 경계 너머 더 좋은 점이 있을 수 있다.
이런 식으로 $h_1$ 의 범위를 넓혀 다시 탐색할 필요가 있다.
(이때 $h_1$ 이외의 parameter는 찾은 최적값으로 고정하고,
$h_1$ 의 범위만 확장하여 재차 탐색)
차원의 저주 측면에서 고려하면 Grid Search보다 Random Search가 유리하다.
다음은 Random Search가 Grid Search보다 성능이 더 좋은 이유를 설명한다.
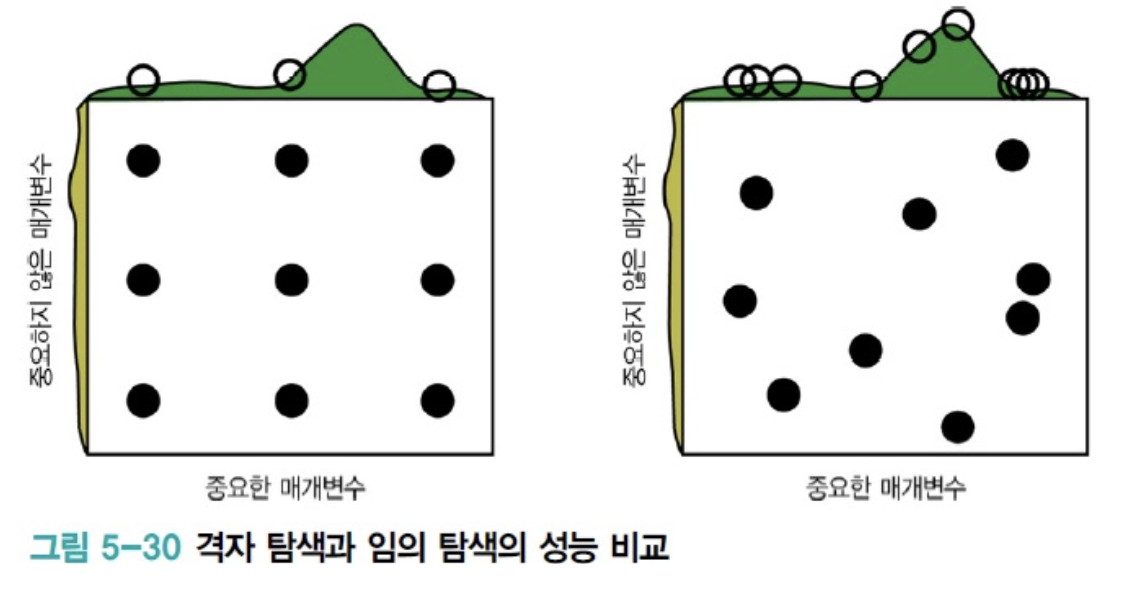
- 녹색 그래프는 가로축의 성능을 뜻하는데, 솟은 부분을 찾아야 좋은 성능을 얻는다.
- Hyper Parameter 최적화라는 관점에서 볼 때,
  가로축 parameter가 새로축 parameter보다 훨씬 중요하다.
  그런데 Grid Search는 가로축의 솟은 부분(좋은 성능)을 비껴갈 가능성이 크다.
Random Search로 최적값 $\hat H$ 를 구한 후 미세조정으로 더 좋은 값을 찾을 수 있다.
미세조정 단계에서는 $\hat H$ 을 중심으로 좁은 범위를 설정한 후
Grid Search 또는 Random Search를 한 번 더 수행한다.
- 첫 번째 단계에서는 큰 간격으로 최적값을 찾고,
- 두 번째 단계에서는 세밀한 간격으로 최적값을 찾는 전략은
  차원의 저주를 피하는 데 효과적이다.

Grid Search와 Random Search는 모두 Heuristic한 방법론이다.
최근에는 더 과학적인 방법론이 제시되고 있다.
- Hyper Parameter의 gradient를 활용하는 기법 [Maclaurin2015]
- bandit problem으로 공식화하는 기법 [Li2016]
- RBF(radial basis function)을 이용한 기법[Diaz2017]
- Spectral 기법 [Hazan2017]
Hyper Parameter Optimization 대한 추천 문헌 :
[Bengio2012, LeCun2012, Bottou2012, Bergstra2012, Goodfellow2016]

Hyungseop Lee

model compression

이전 포스트

[Chap 5] 딥러닝 최적화

[Study] Machine Learning

목적함수 : Cross Entropy & Log Likelihood

MSE 단점

MSE가 목적함수로서 부적절한 상황

Cross Entropy

Softmax

Log Likelihood

성능 향상을 위한 요령

데이터 전처리

정규화

One-Hot Encoding

가중치 초기화

Momentum

Adaptive Learning Rate

AdaGrad

RMSProp

Adam

Momentum & Adaptive Learning Rate

Activation Function

Batch Normalization

Covariate Shift 현상

Batch Normalzation 개념

Batch Normaliztion 장점

규제의 필요성과 원리

Overfitting에 빠지는 이유와 피하는 전략

규제의 정의

규제 기법

Weight Penalty

1. L2-norm (weight decay)

Ridge Regression

MLP와 DMLP에 적용

2. L1-norm

Lasso Regression

Early Stopping

Data Augmentation

dropout

앙상블 기법

Hyper Prameter 최적화

Grid Search & Random Search

[PyTorch 실습] MLP, CNN

0개의 댓글

[Study] Machine Learning