[PyTorch 실습] MLP, CNN

Hyungseop Lee·2023년 4월 6일

[Study] Machine Learning

목록 보기

8/9

실습을 위한 사전지식

Softmax

Softmax 함수는 Multi Class Classification model을 만들 때 사용한다.
결과를 확률로 해석할 수 있게 변환해주는 함수로 높은 확률을 가지는 class로 분류한다.
이는 결과값을 정규화시키는 것으로도 생각할 수 있다.
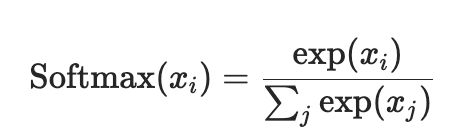
- 미분이 가능하도록 exp를 취함
- $\Sigma_j exp(x_j)$ : 요소별 exp를 취한값의 총합
- $exp(x_i)$ : 해당 요소에 exp를 취한 값

Cross Entropy

Cross Entropy는 두 확률 분포 간의 유사도를 계산하는 방법 중 하나이다.
Classification 문제에서는 Cross Entropy가 손실 함수로 자주 사용된다.
이 때, 예측값과 실제값의 분포 간의 차이를 계산하여,
분류 모델이 예측을 잘못한 경우에 높은 손실 값을 나타내고,
예측을 잘한 경우에는 낮은 손실 값을 나타낸다.

$H(t, y) = -∑ t_i log(y_i)$

$x$ : 입력값

$t$ : 실제값

$y$ : 예측값

PyTorch에서 CrossEntropyLoss는 (LogSoftmax + NLLLoss)로 구현되어 있다.
- LogSoftmax
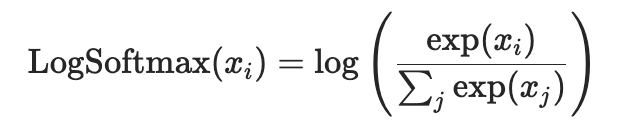
- NLLLoss(Negative Log Likelihood Loss)
  https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html

optimizer

https://pytorch.org/docs/stable/optim.html

weight initialzation

torch.nn.init.normal_()

reference : https://pytorch.org/docs/stable/nn.init.html#torch.nn.init.normal_

torch.nn.init.normal_(tensor, mean=0.0, std=1.0)
- tensor (Tensor) – an n-dimensional torch.Tensor
- mean (float) – the mean of the normal distribution
- std (float) – the standard deviation of the normal distribution

MLP, MNIST Classification

Hyper Parameter에 따른 Loss Function 값과 accuracy를 구하여 시각화해본다.

Hyper Parameter - Learning Rate

training_epochs = 50, batch_size = 100로 똑같은 조건에서
Learning Rate만 바꿔서 Loss값 측정하여 해석하기.

`LR = 0.1`

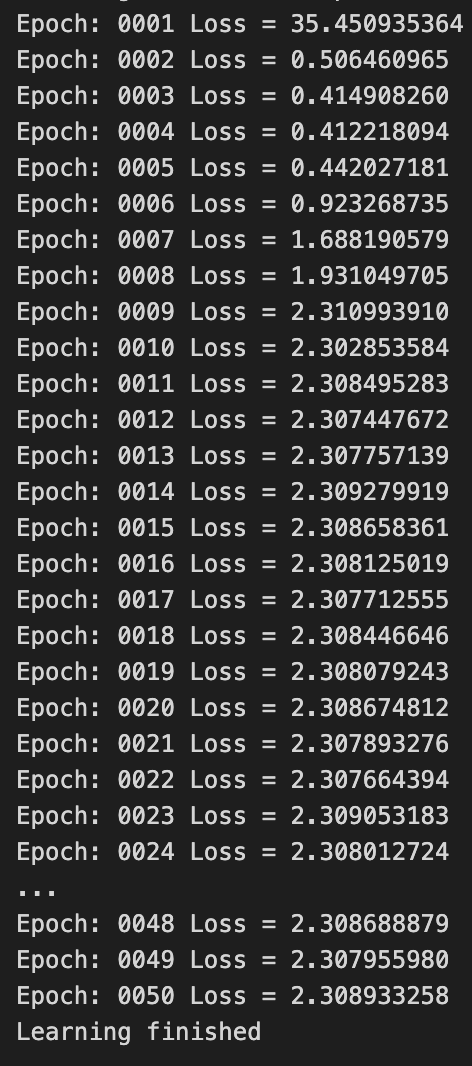
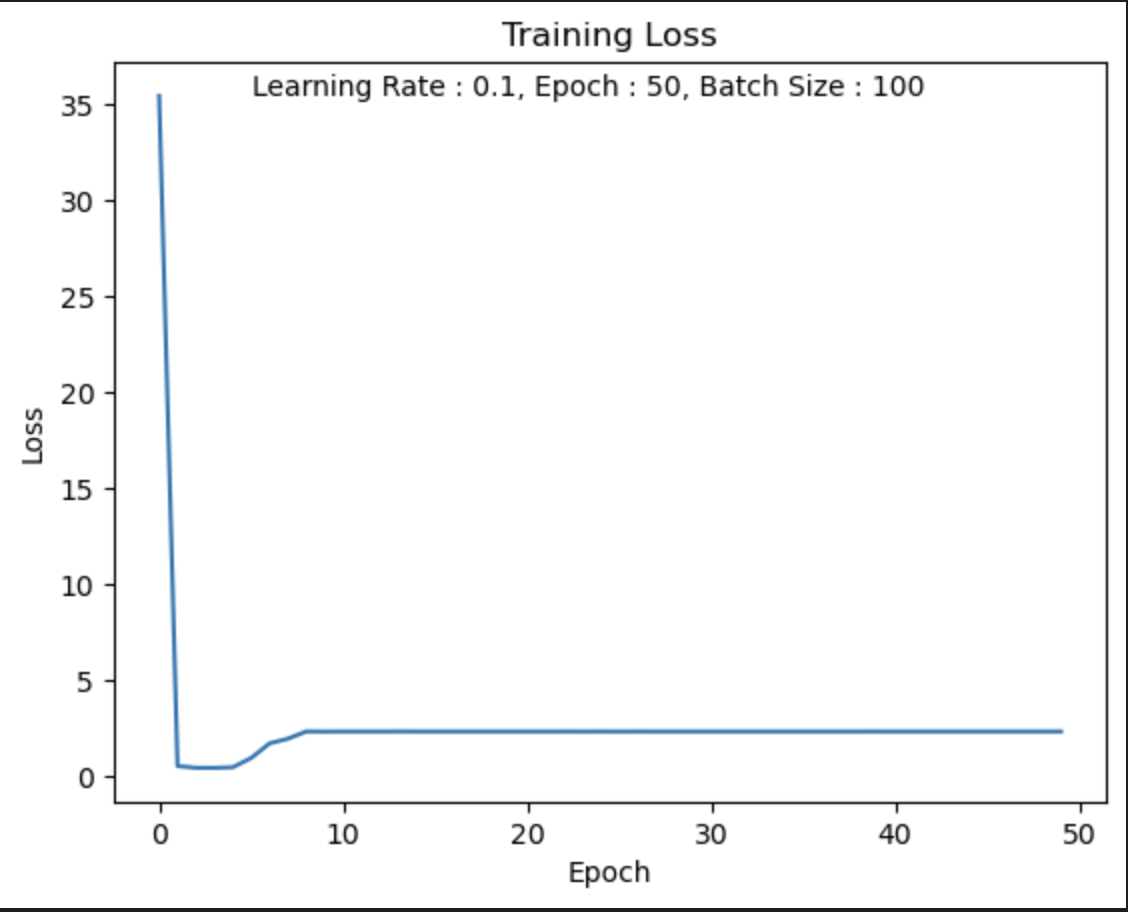
accuracy = 0.10이 나왔었다

나의 생각 :
Learning Rate를 크게 했기 때문에 Global Minimum에 가지 못하고 발산하여
Local Minimum(2.30x)에 수렴하여 못 빠져나오는 것 같다.
== 잘못 학습된 것 같다.

`LR = 0.01`

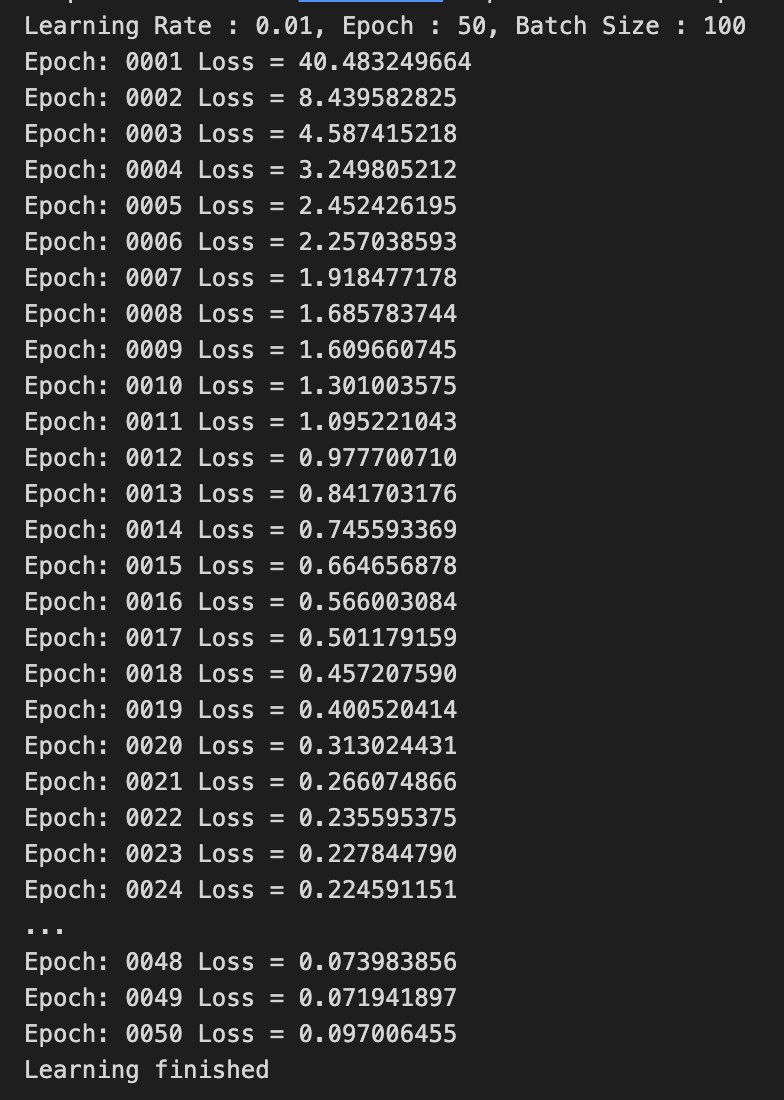
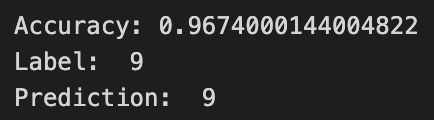
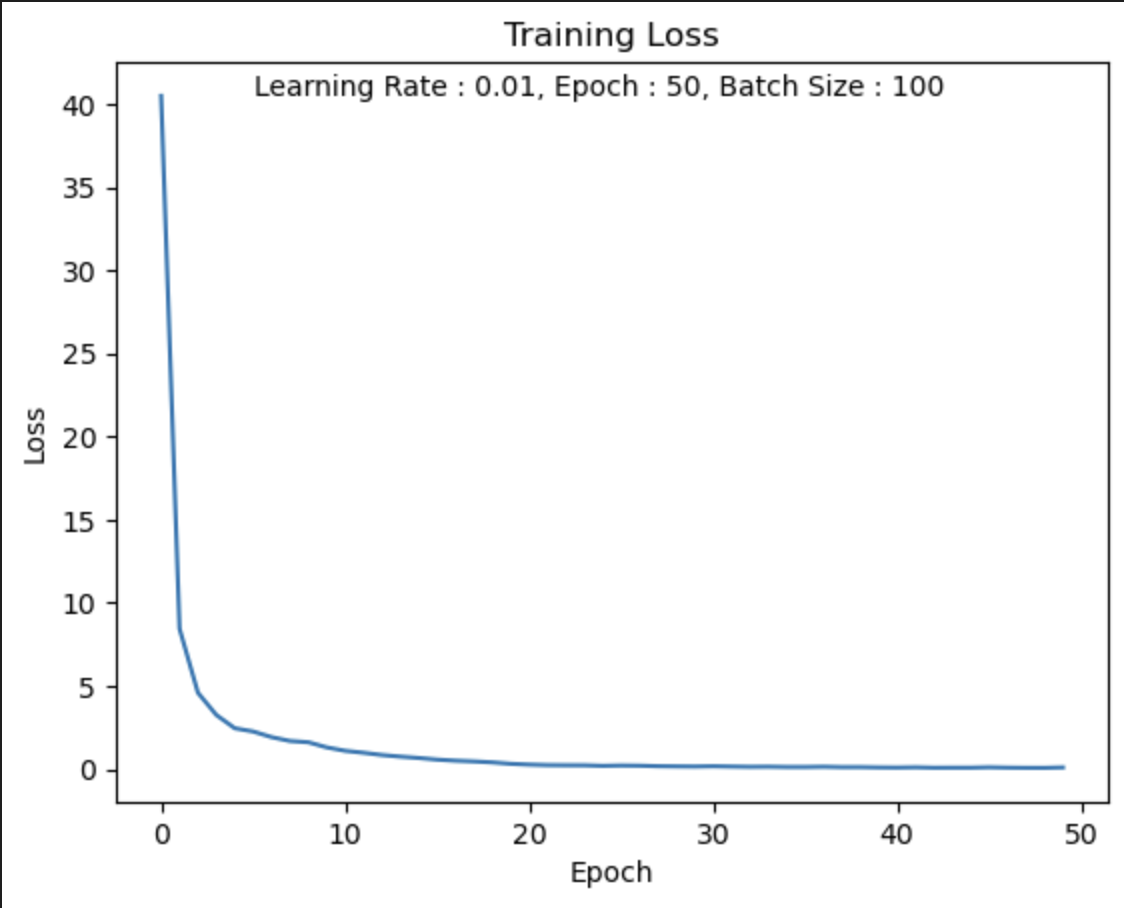
나의 생각 :
Loss값이 빠르게 0으로 수렴하는 것을 알 수 있고,
적절한 Learning Rate를 부여함으로써 학습이 잘 된 것같다.

`LR = 0.001`

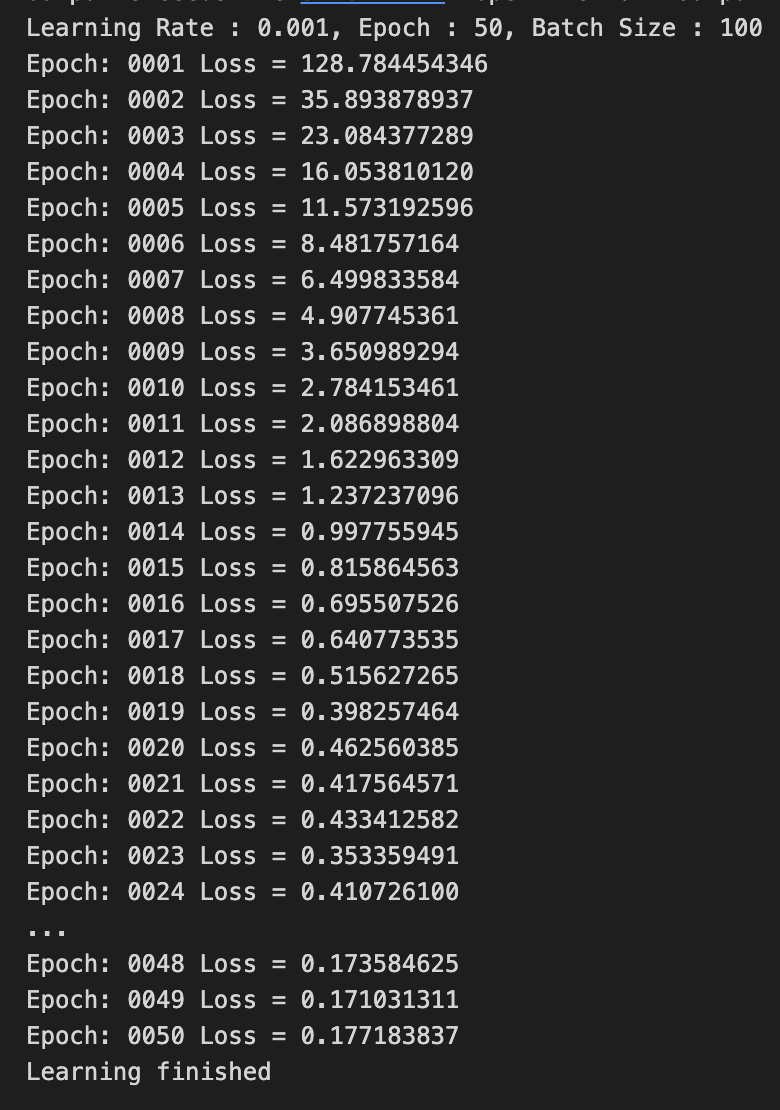
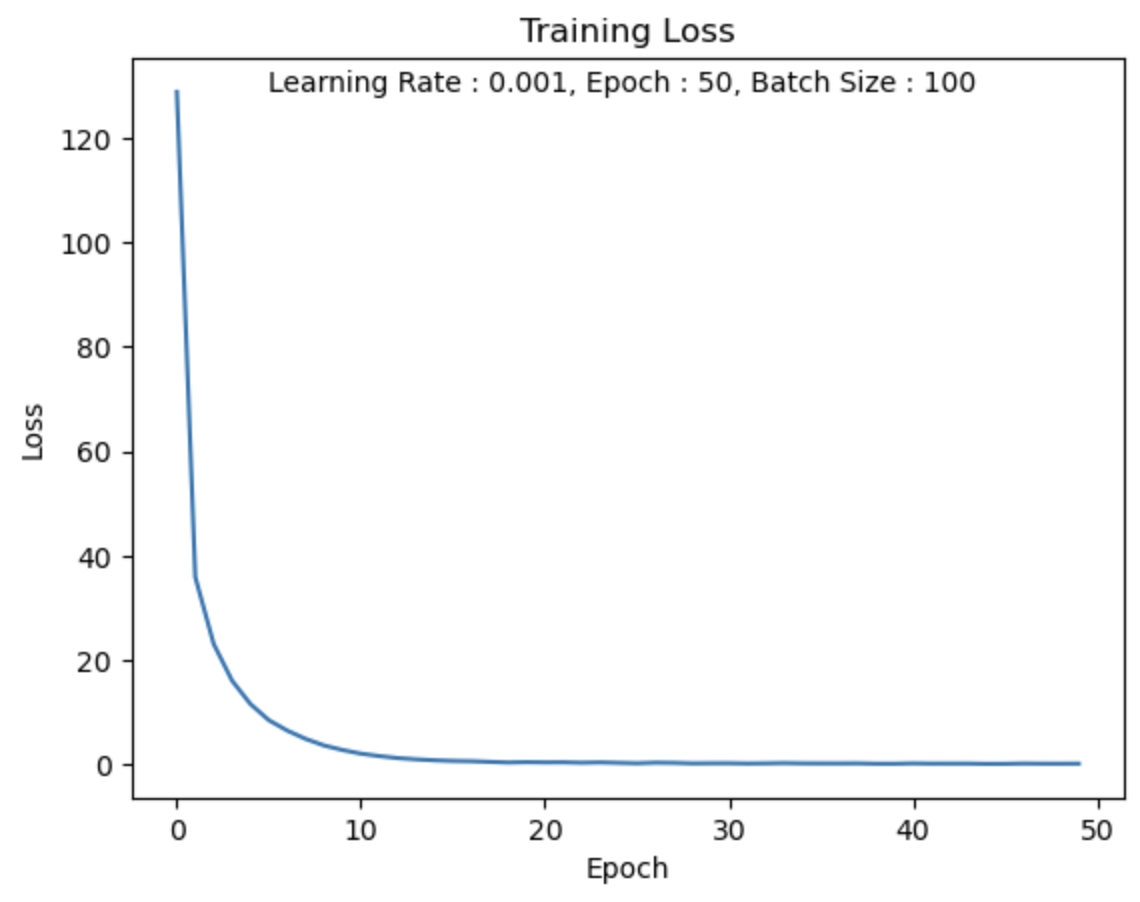
Loss값이 빠르게 0으로 수렴하는 것을 알 수 있고,
적절한 Learning Rate를 부여함으로써 학습이 잘 된 것같다.
LR = 0.01과 굳이 차이를 보자면 좀 더 부드럽게 Loss값이 줄어드는 것을 알 수 있다.
만약 Epoch이 충분히 컸다면 이 차이는 더 명확히 보였을 것 같다.

`LR = 0.0001`

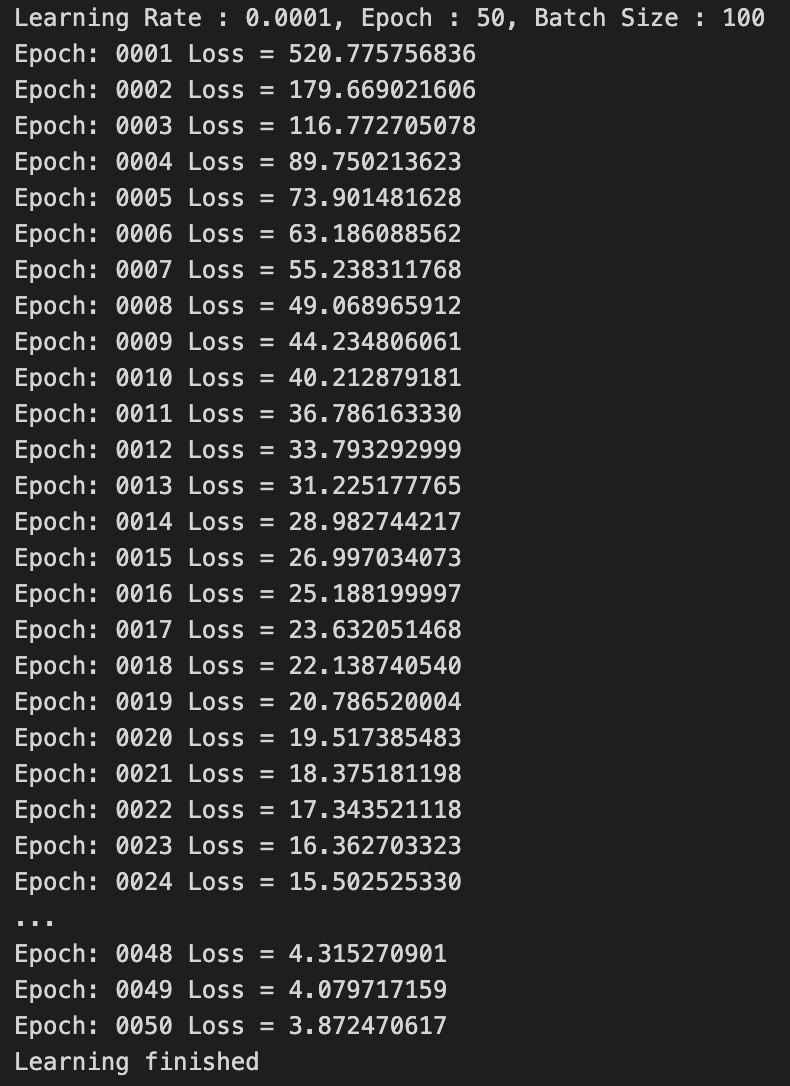
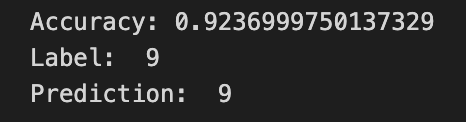
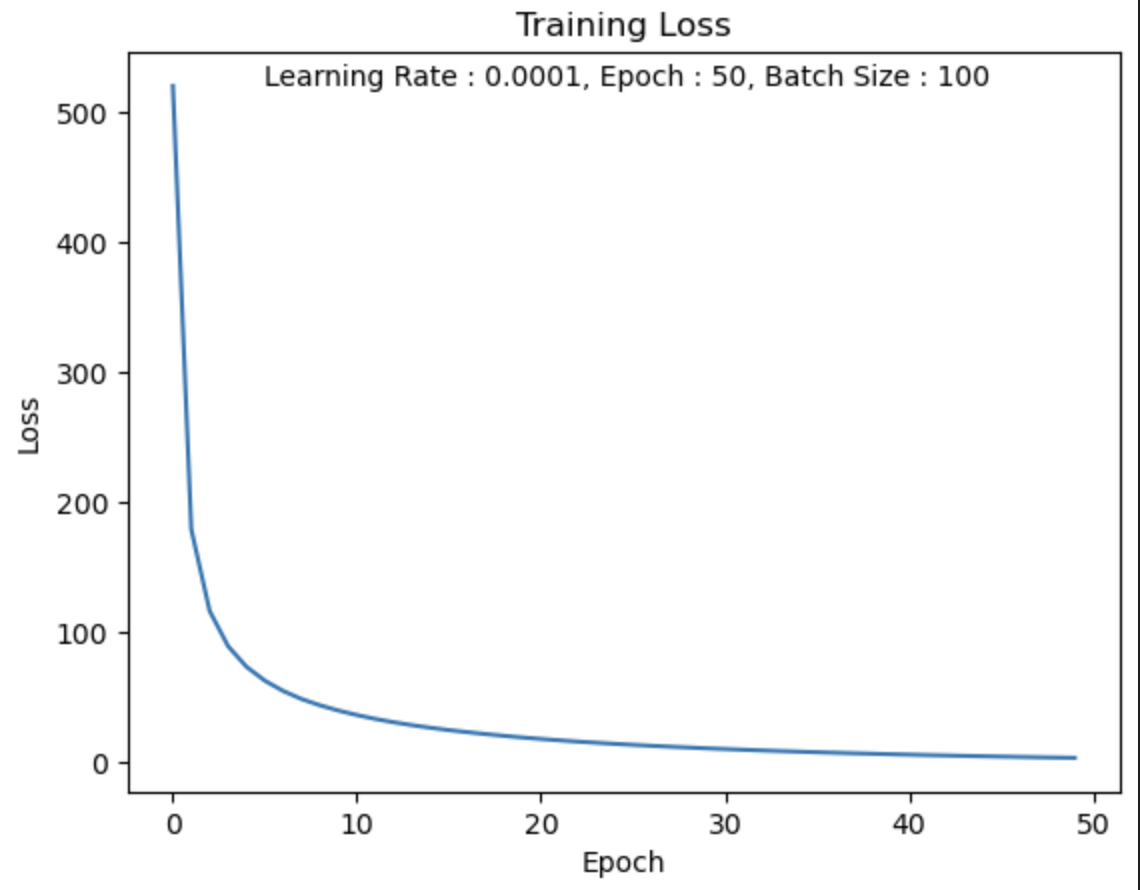
나의 생각 :
LR = 0.01, 0.001보다 학습이 천천히 진행된 것을 알 수 있다.
하지만 학습이 잘못되지 않은 것은 아니다.
Epoch가 충분히 컸다면 Loss값은 0에 더욱 수렴되어 Accuracy가 더 높았을 것이다.

한 눈에 살펴보고 분석하기

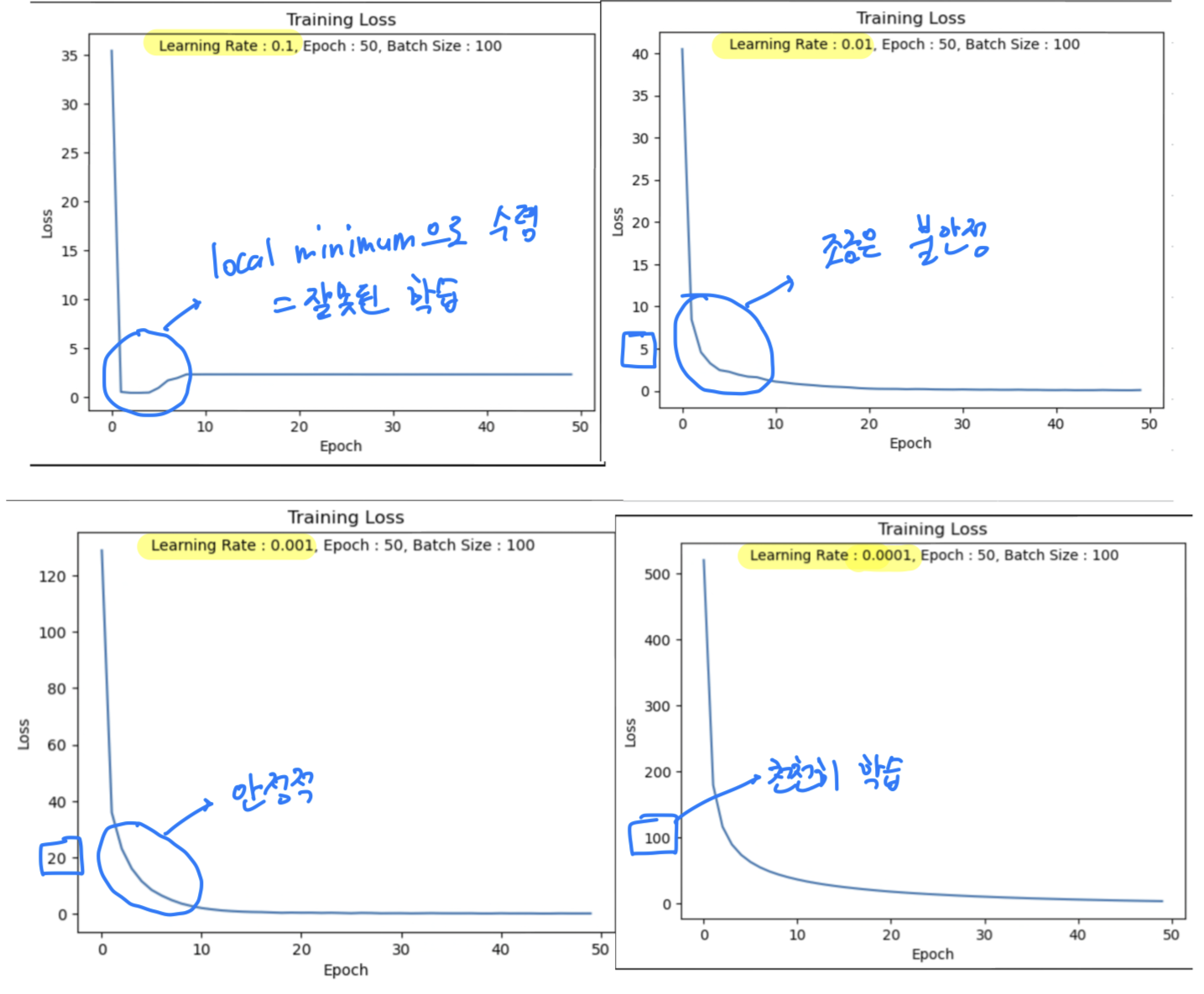
Hyper Parameter - Epoch

learning_rate = 0.0001, batch_size = 100로 똑같은 조건에서
total_epochs만 바꿔서 Loss값 측정하여 해석하기.

Epoch = 5

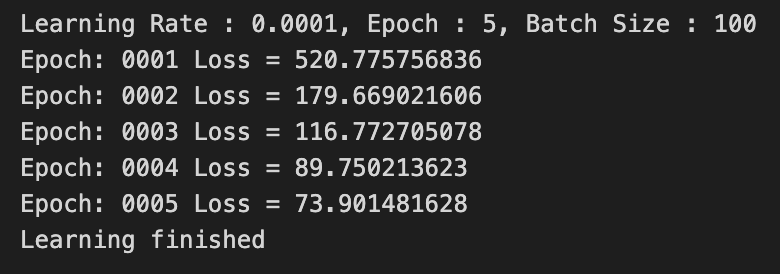
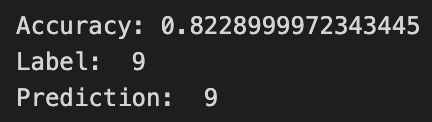
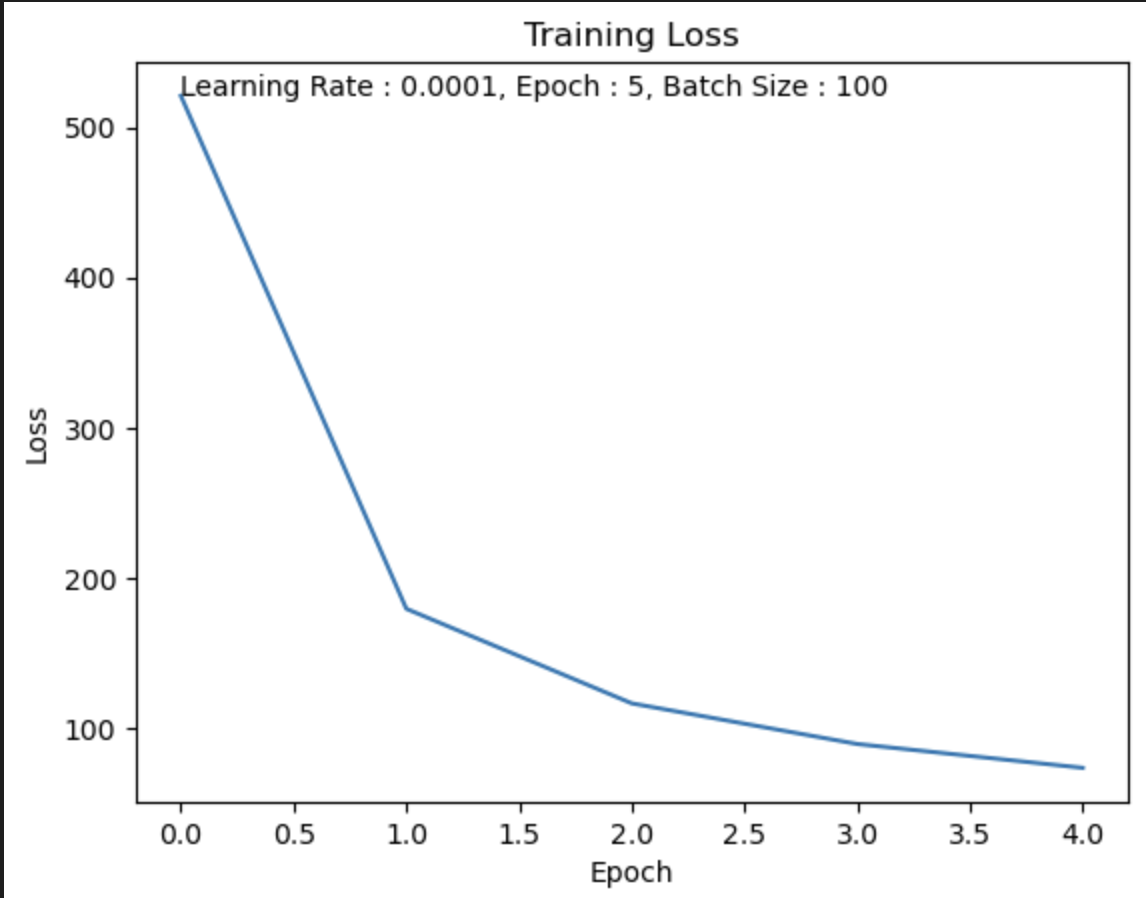
나의 생각 :
forward 계산과 weight update 과정을 5번만 했기 때문에 제대로된 학습을 하지 못했다.
Epoch을 더 크게 했다면 Loss가 0에 더 수렴해갈 것이다.

Epoch = 30

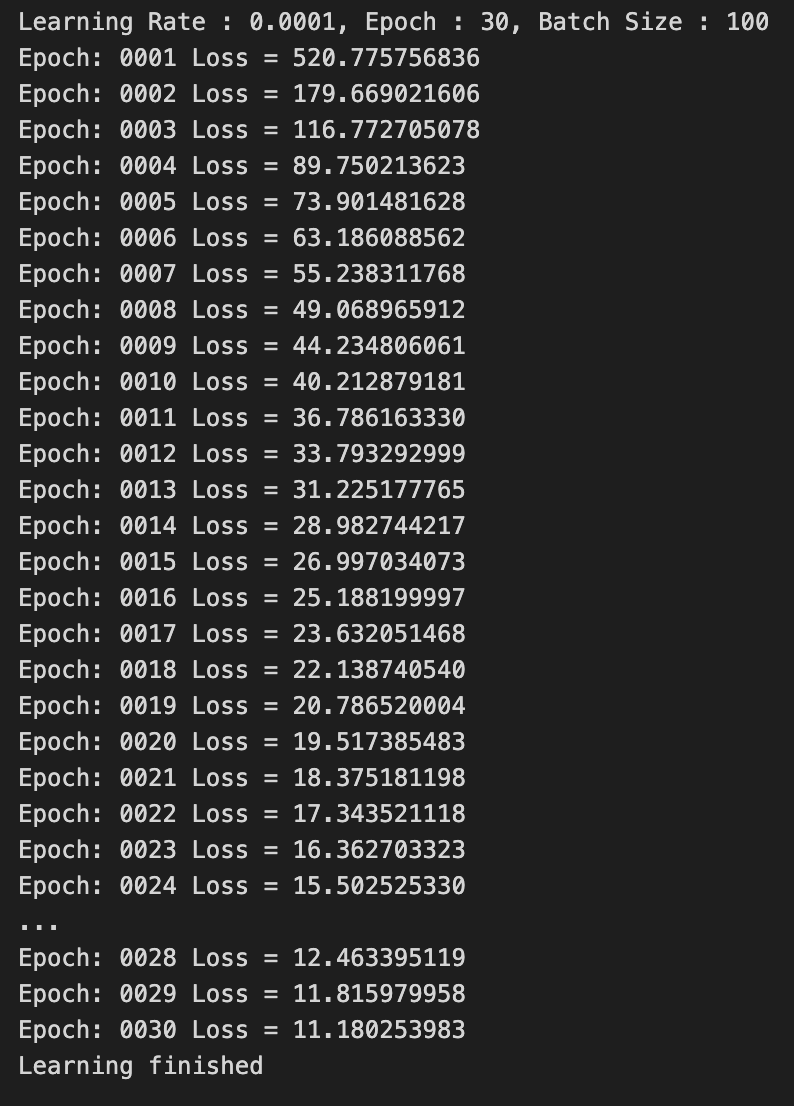
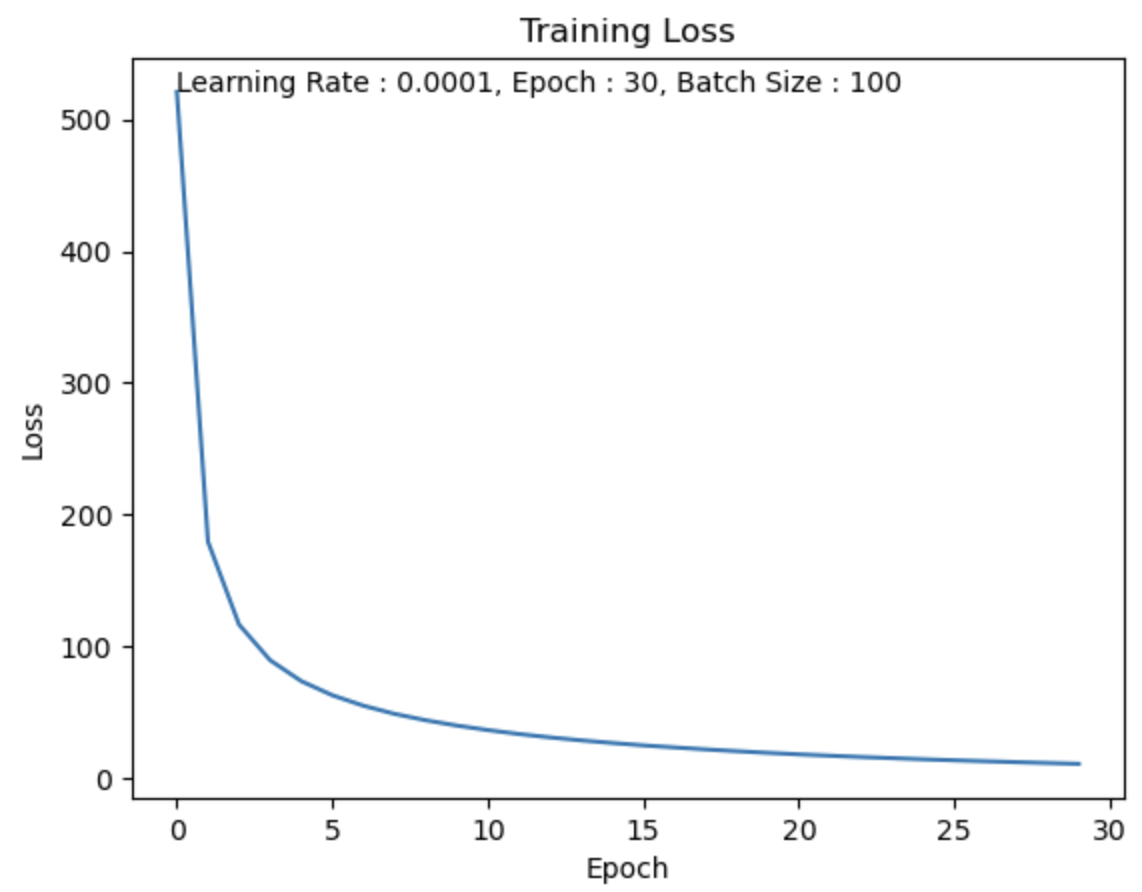
나의 생각 :
forward 계산과 weight update 과정을 5번보다는 더 많이 했기 때문에
Epoch=5일 때보다제대로된 학습을 했다.
하지만 여전히 Epoch 수가 부족하기 때문에 Loss가 0에 가까워지기엔 멀다.
Epoch을 더 크게 했다면 Loss가 0에 더 수렴해갈 것이다.

Epoch = 50

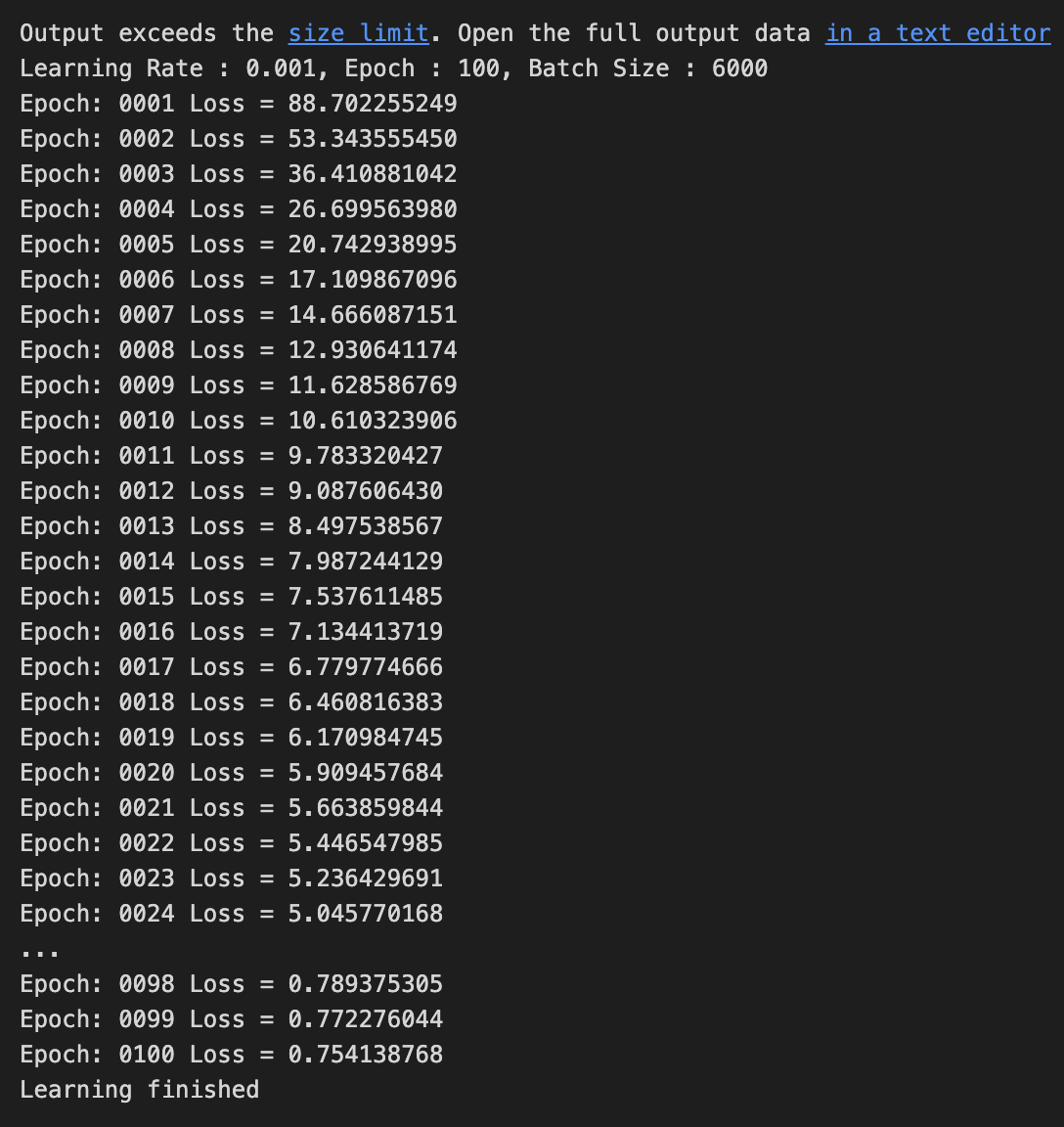
Epoch = 100

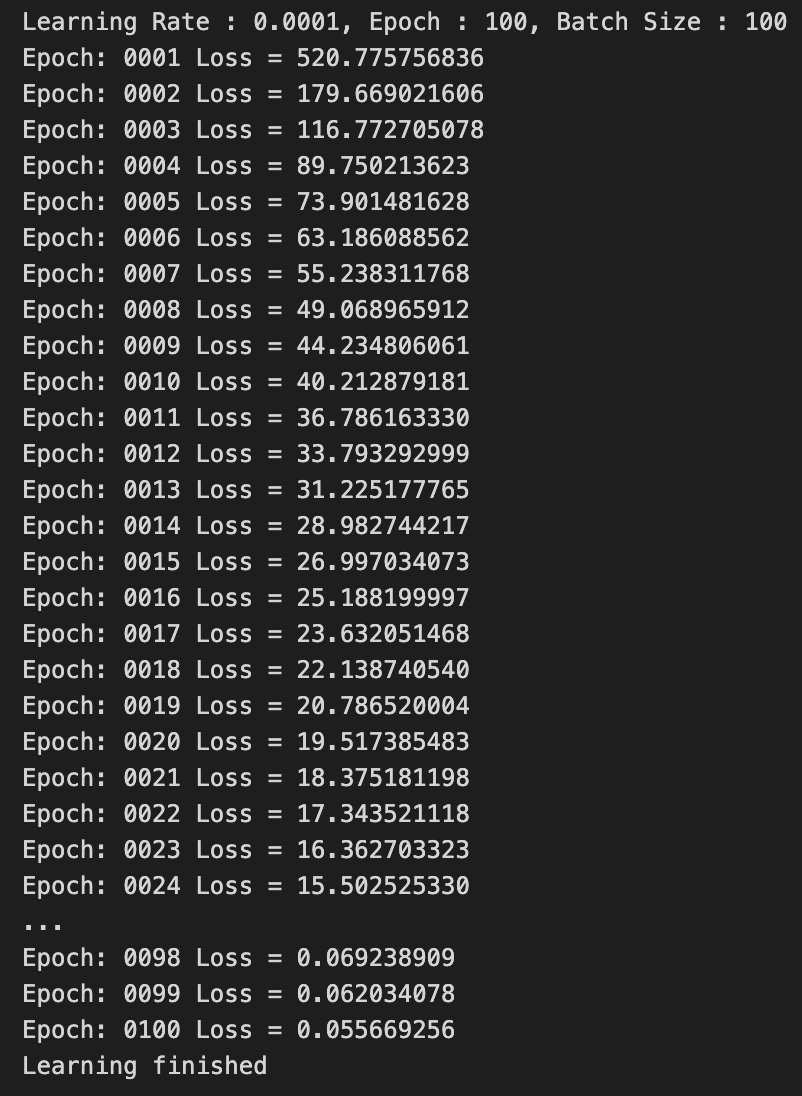
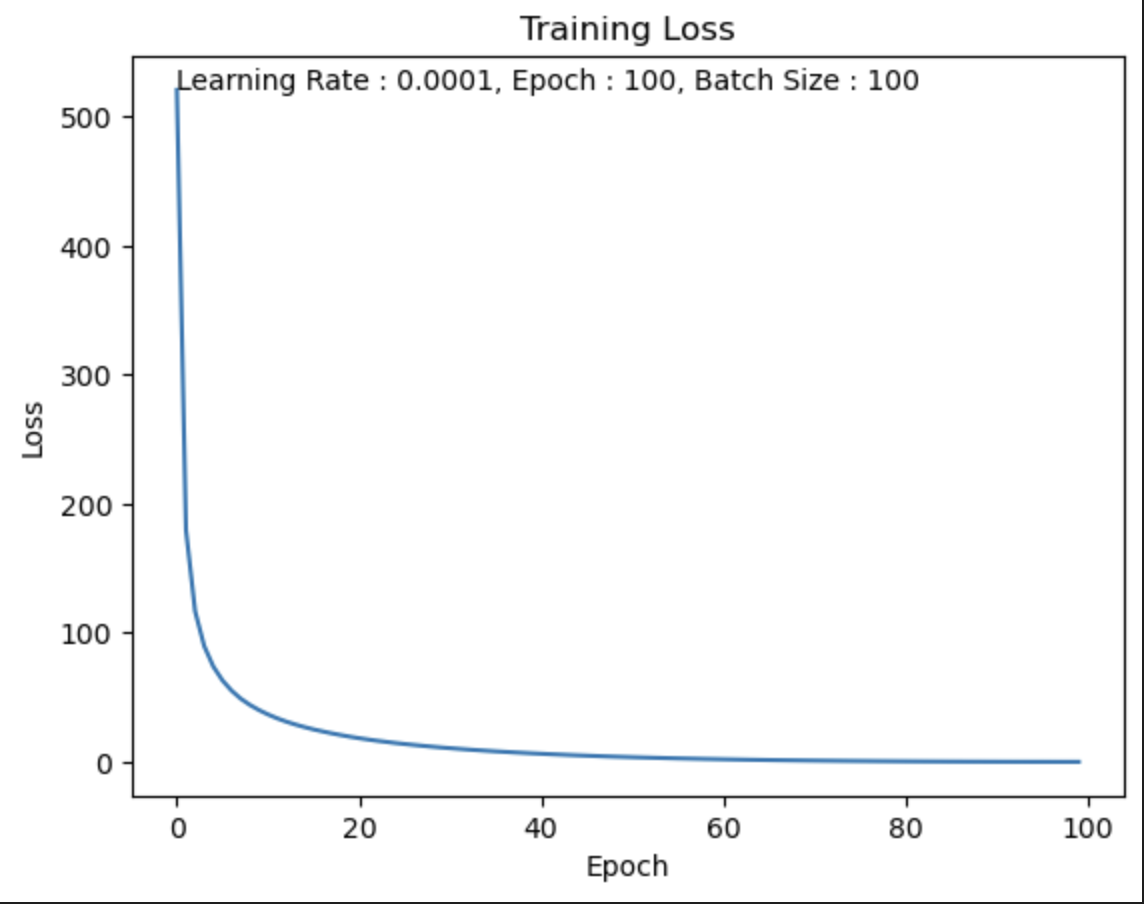
한 눈에 살펴보고 분석하기

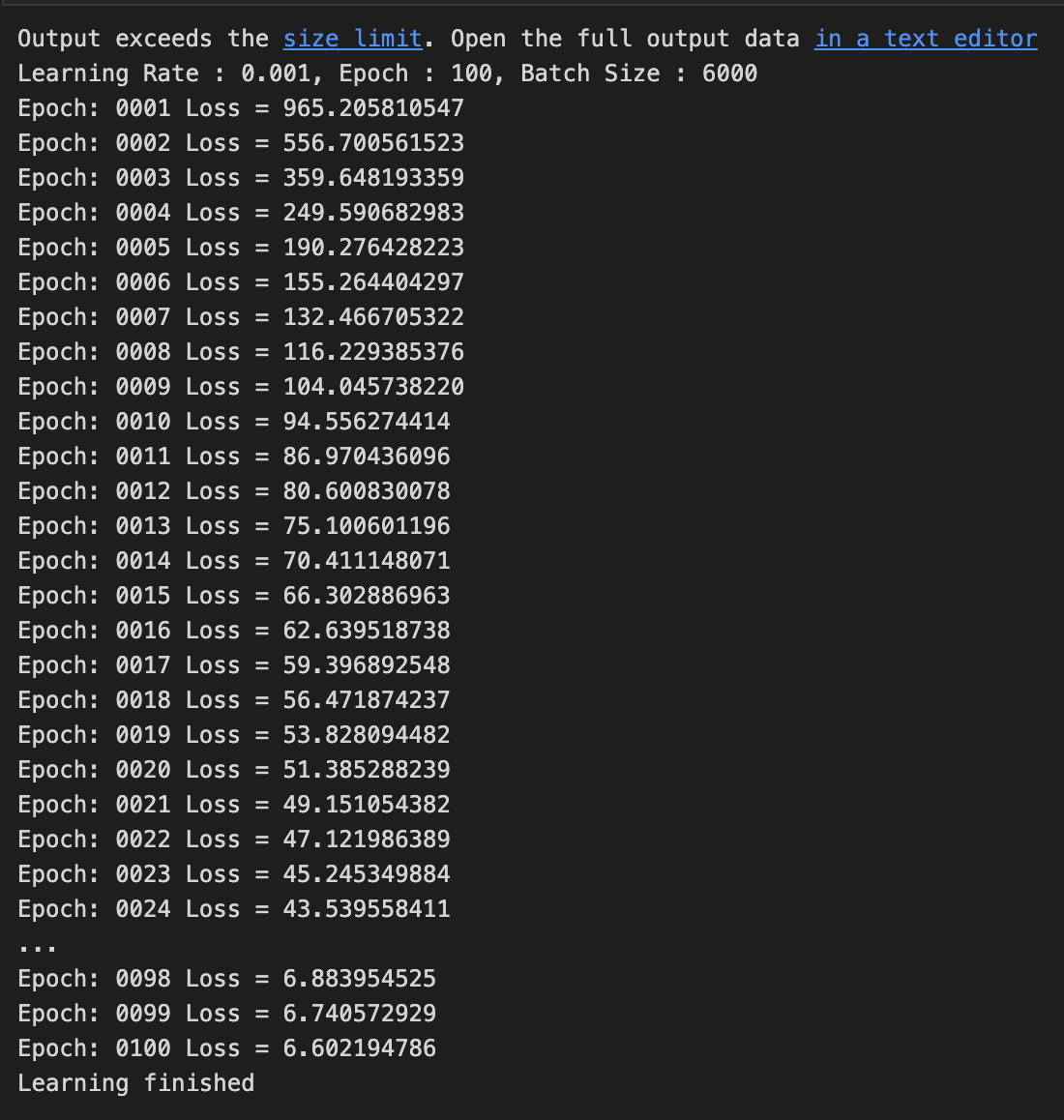
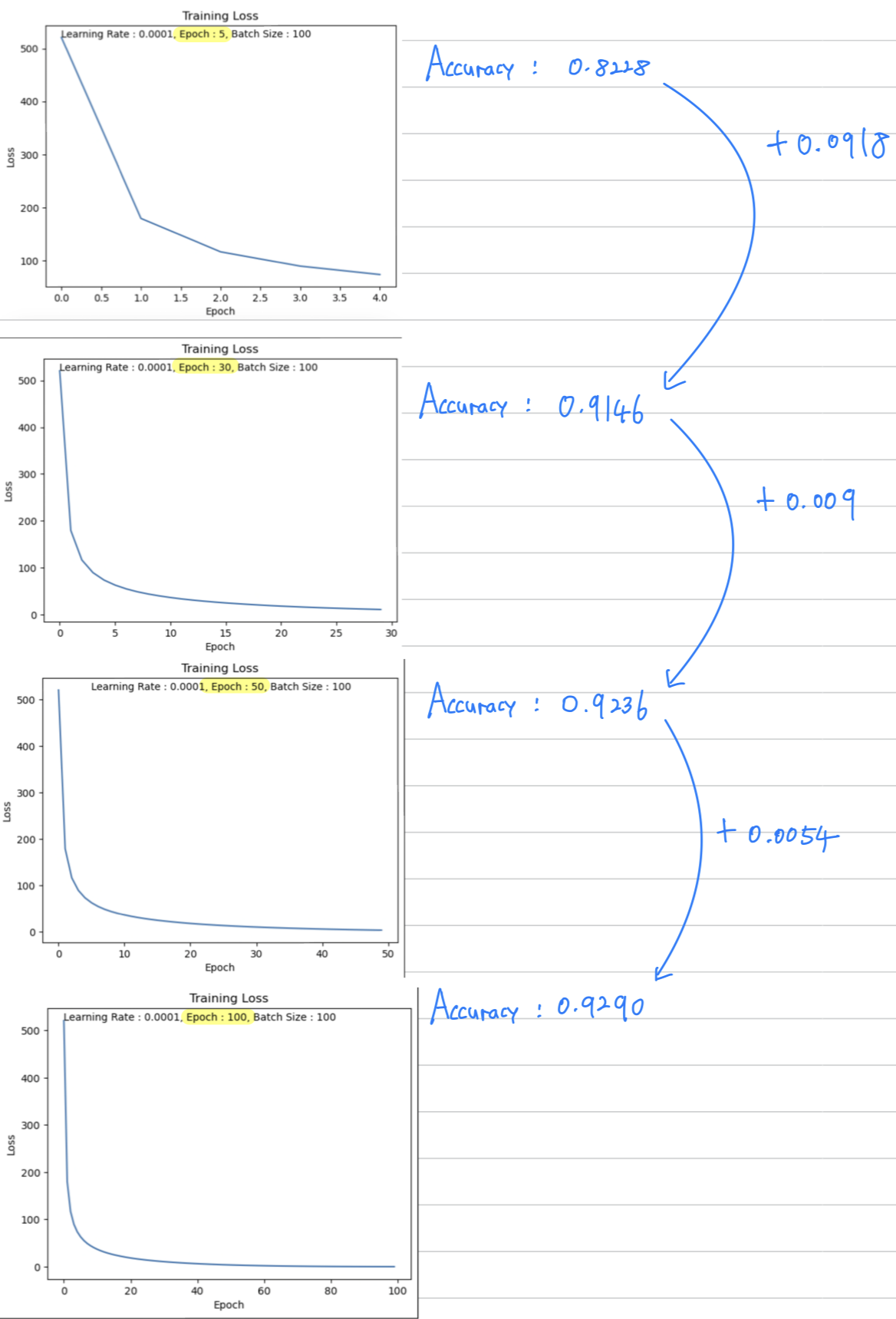1. Epoch 수를 늘리면 Train Set에 대한 학습이 충분히 되어 Train Set에 대해서 Loss값이 0에 수렴해진다.
2. Epoch 수를 늘리면 Train Set에 대한 Accuracy가 점점 증가하긴 하는데,
증가하는 크기가 점점 감소한다.
(+0.0918 ➡️ +0.009 ➡️ +0.0054 ➡️ ... ➡️ -0.00?)
== Test Set에만 Overfitting되고 있다.
== Epoch 수를 매우 많이 늘린다면 Accuracy 증가가 아니라 감소가 되어 Accuracy가 작아질 수 있다.
3. Epoch이 클수록 학습 시간이 오래 걸린다.

Hyper Parameter - Batch Size

Batch Size = 10

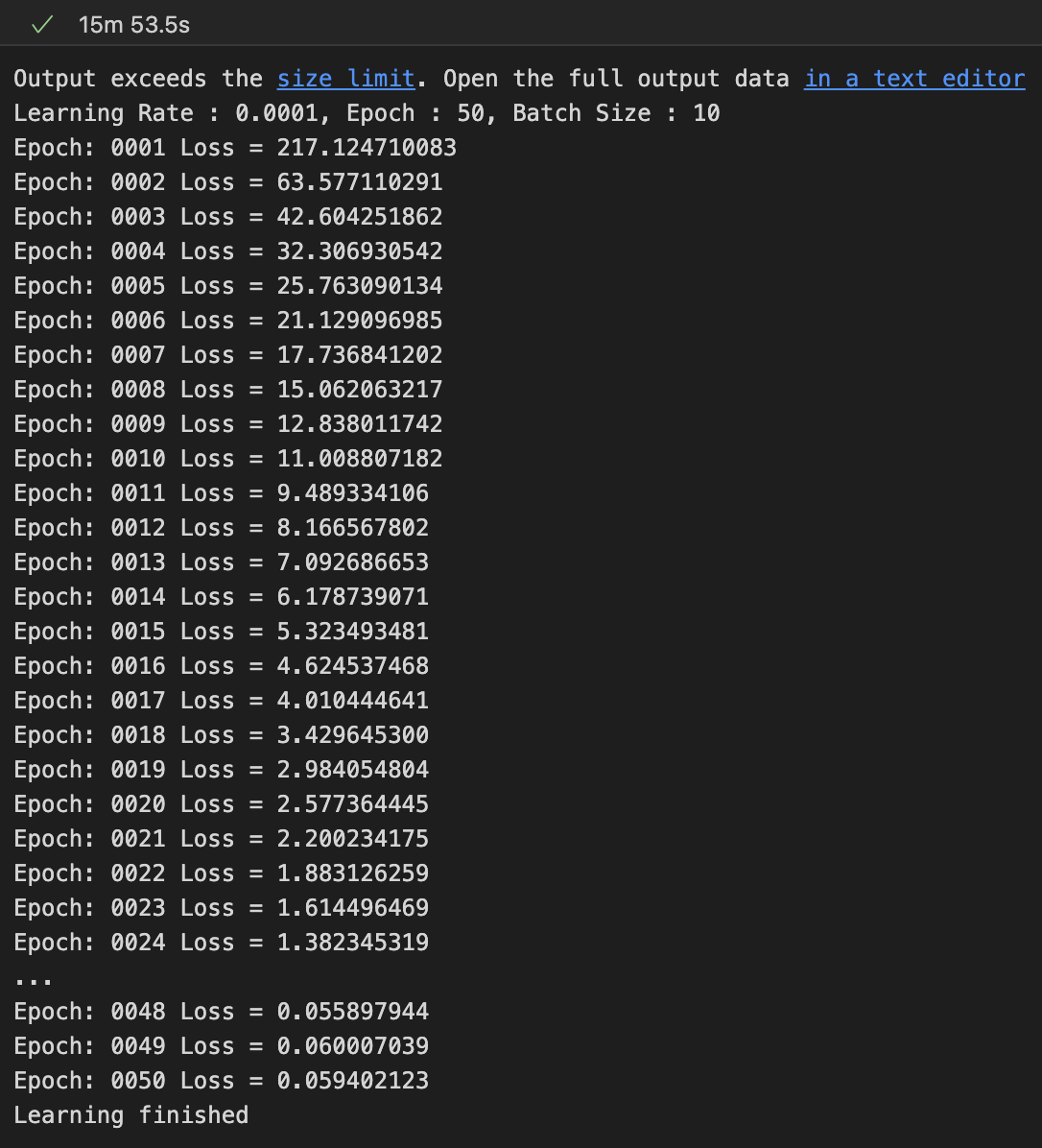
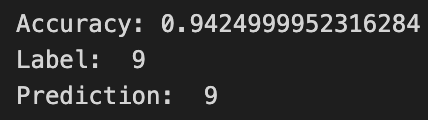
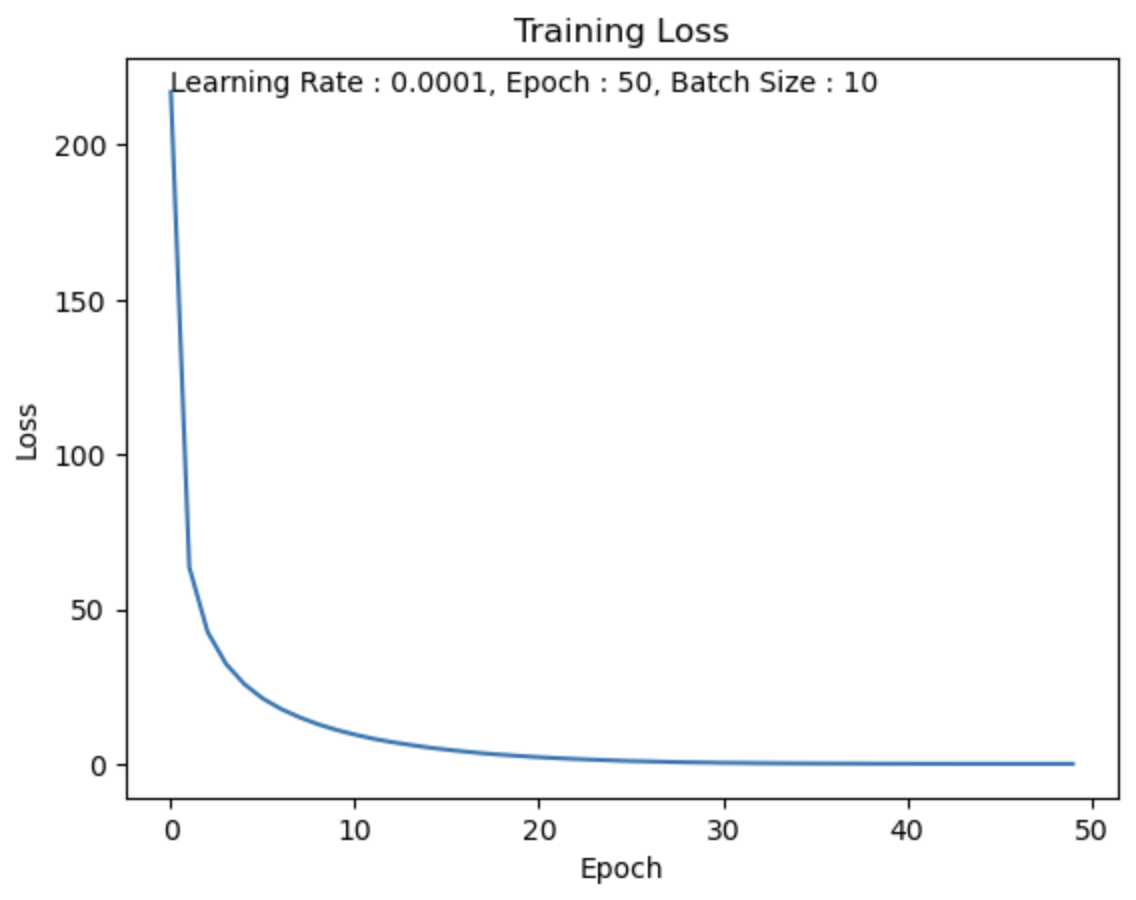
batch size를 10로 했을 때, 15분 53초.
Test Set의 데이터가 60,000개이고 batch size를 10로 했기 때문에
1 Epoch에 6,000번 반복을 수행한다.

Batch Size = 30

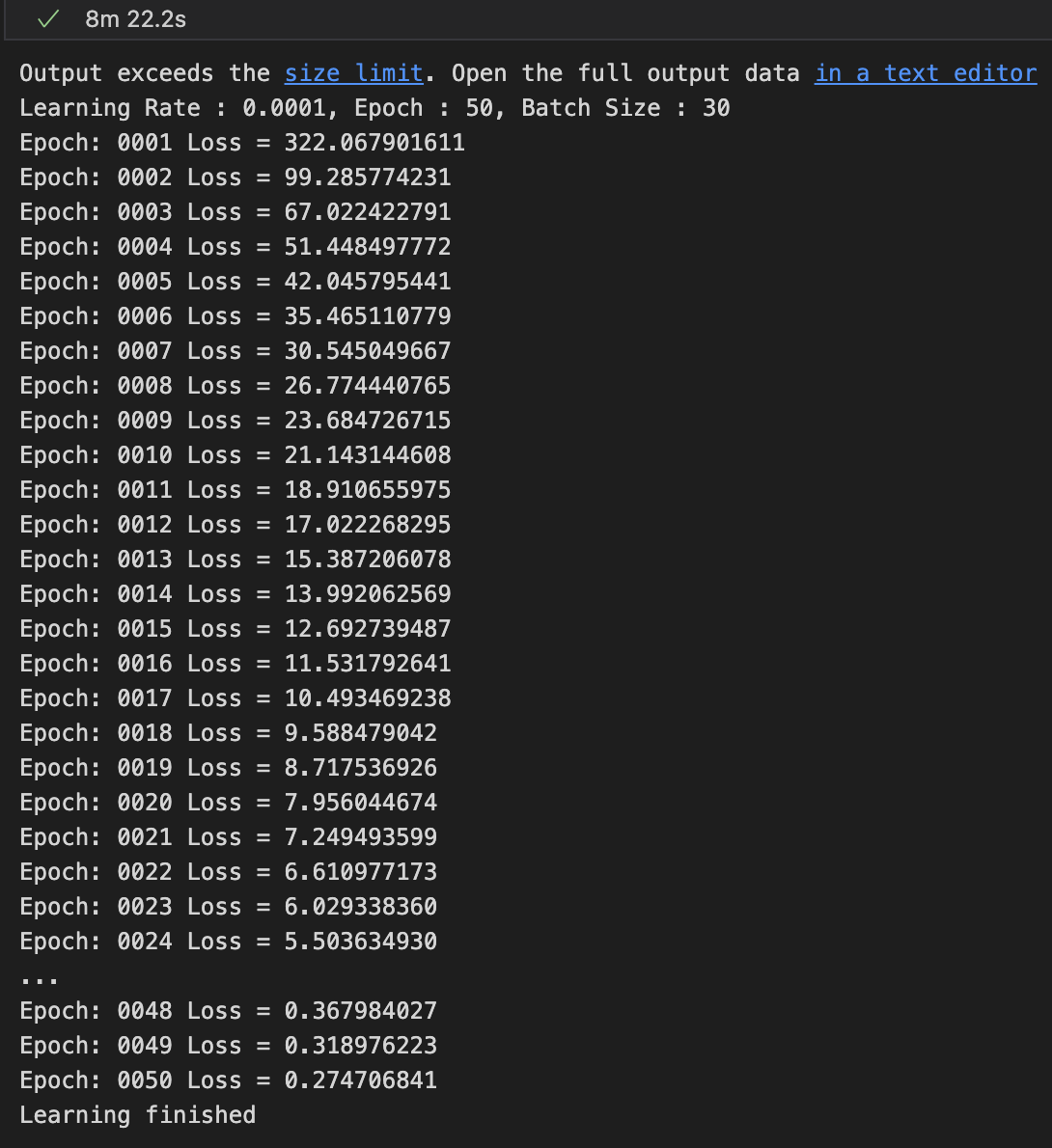
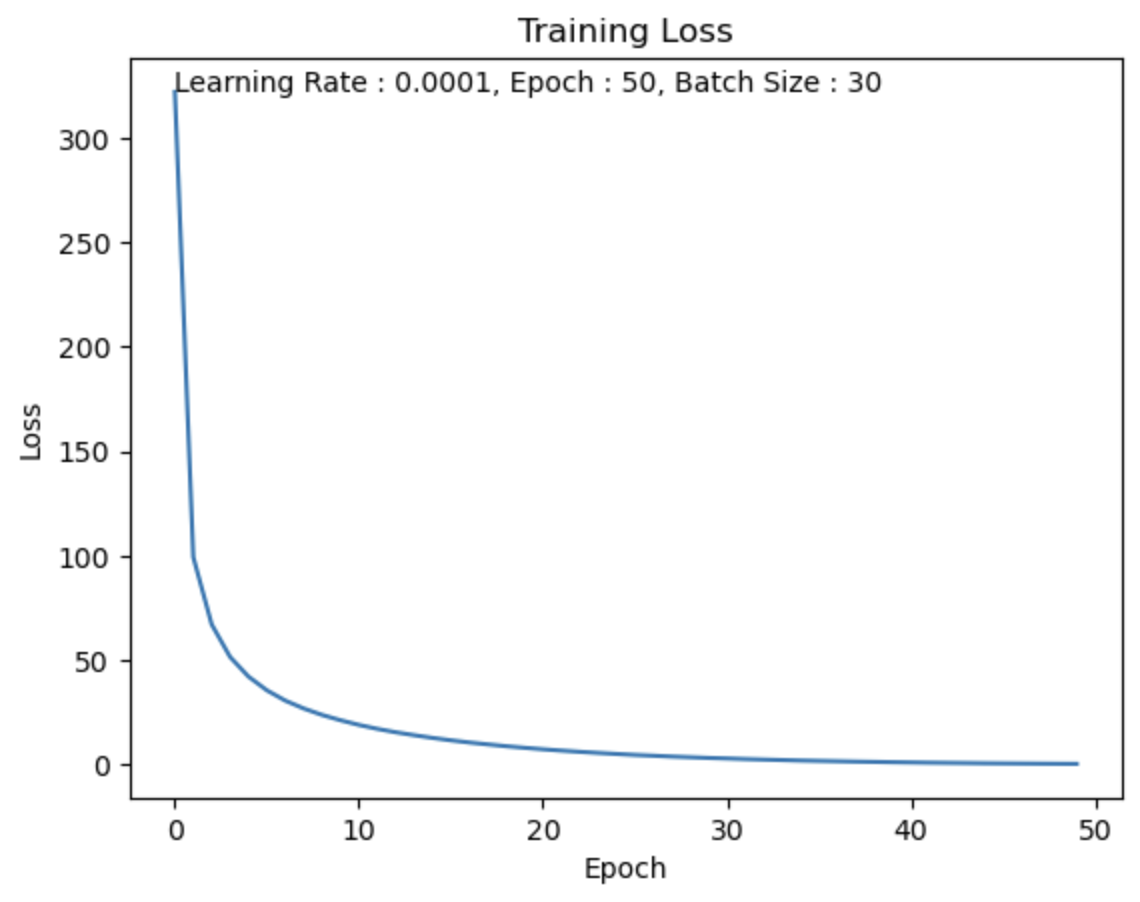
batch size를 30로 했을 때, 8분 22초.
Test Set의 데이터가 60,000개이고 batch size를 30로 했기 때문에
1 Epoch에 2,000번 반복을 수행한다.

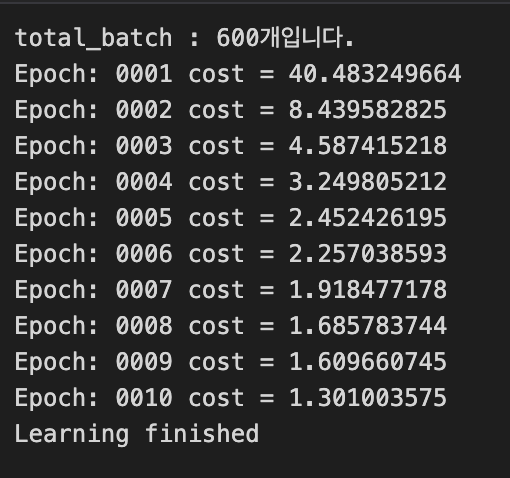
Batch Size = 100

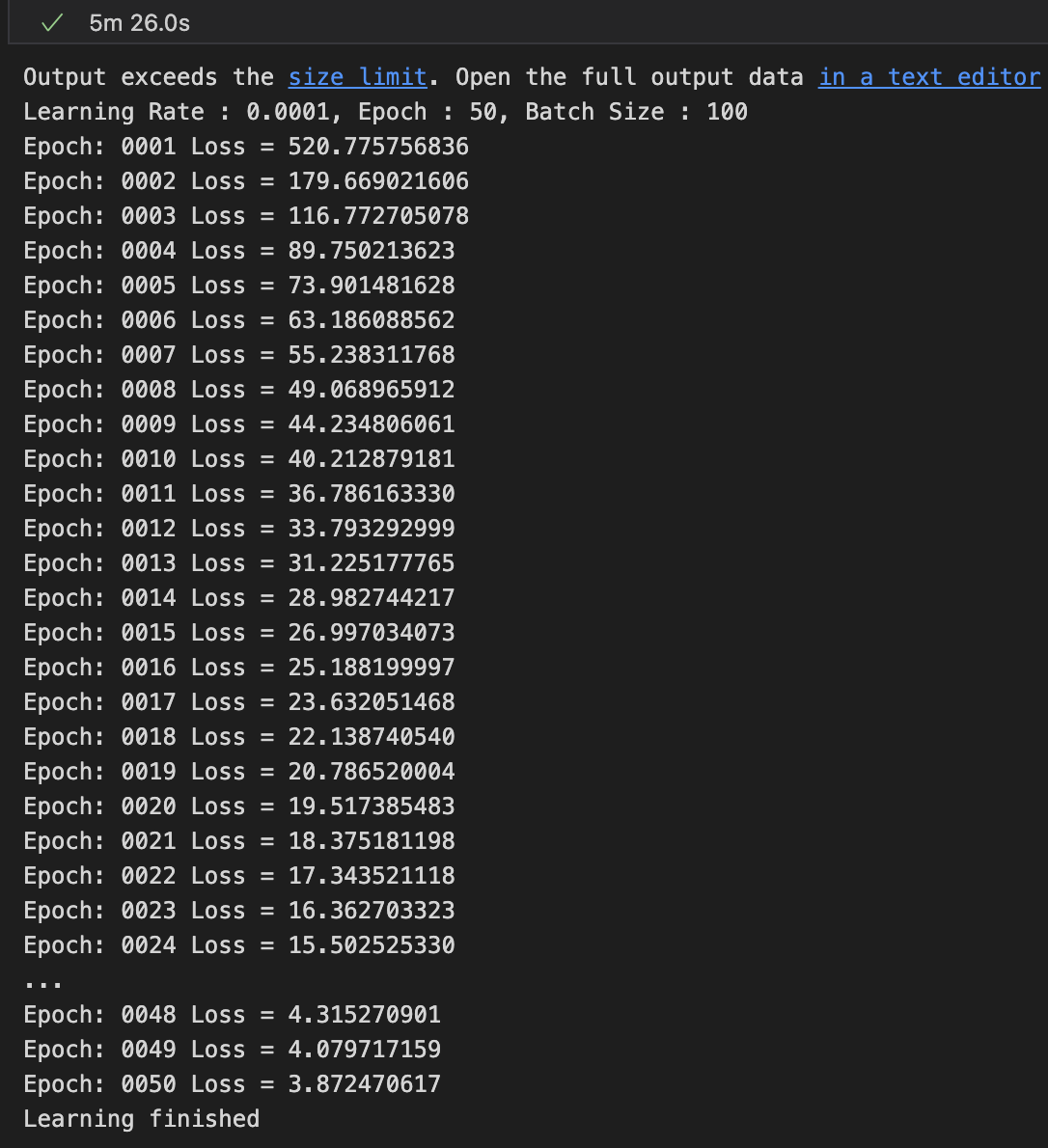
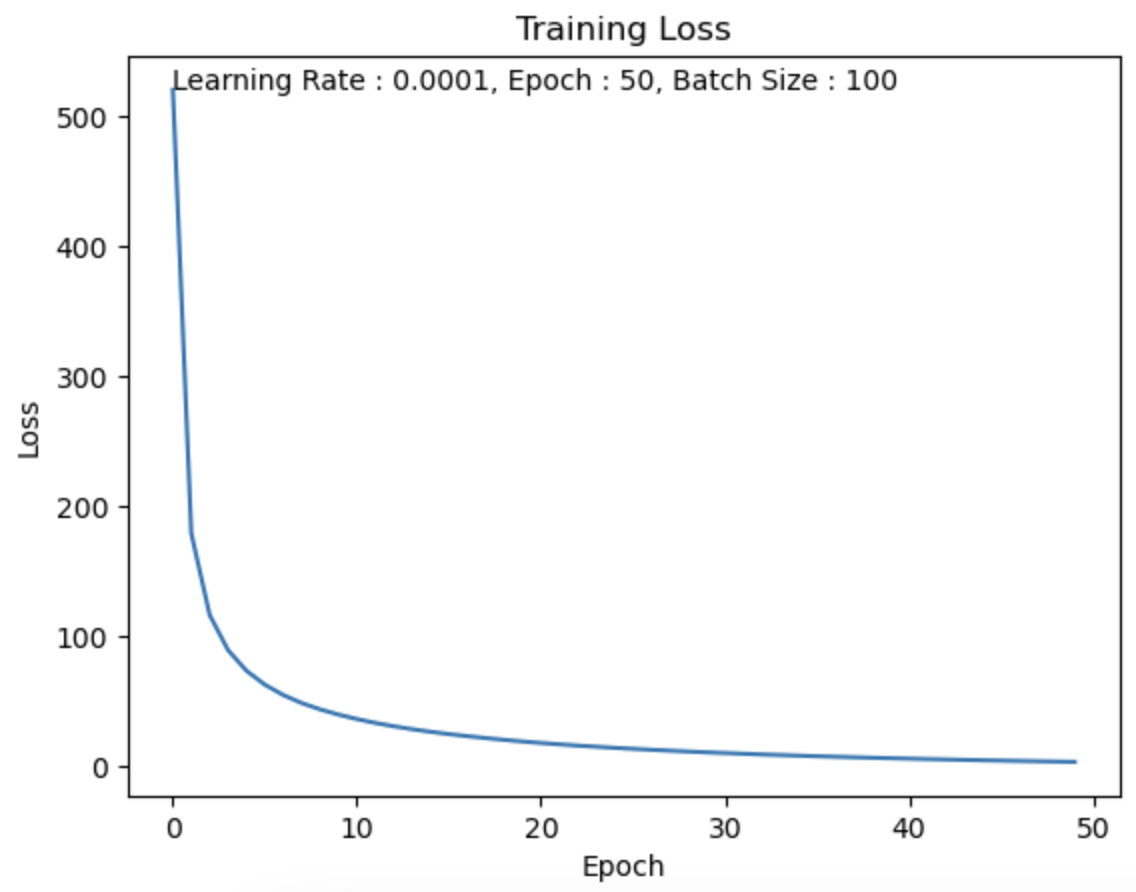
batch size를 100로 했을 때, 5분 26초.
Test Set의 데이터가 60,000개이고 batch size를 100로 했기 때문에
1 Epoch에 600번 반복을 수행한다.

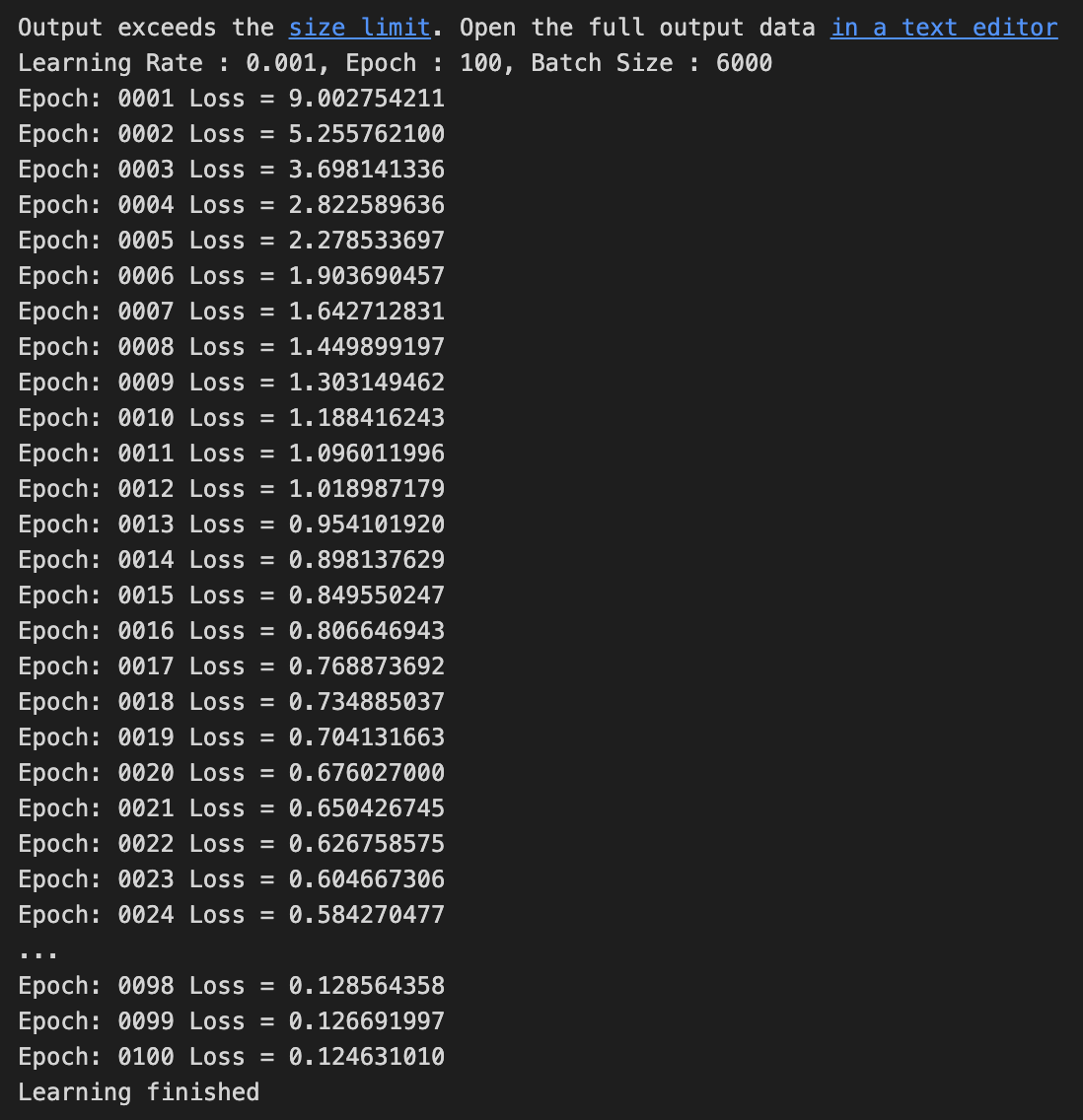
Batch Size = 1000

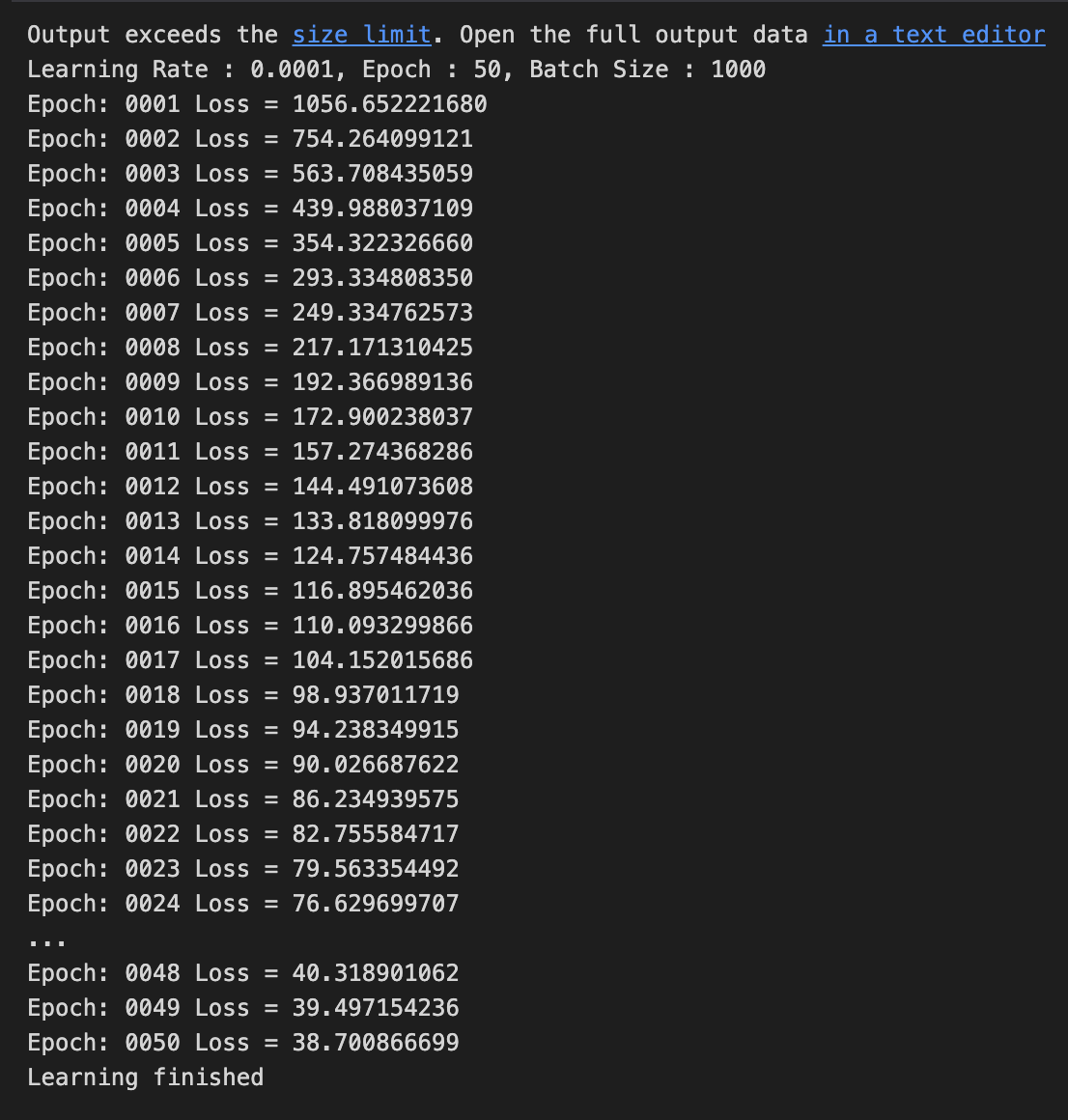
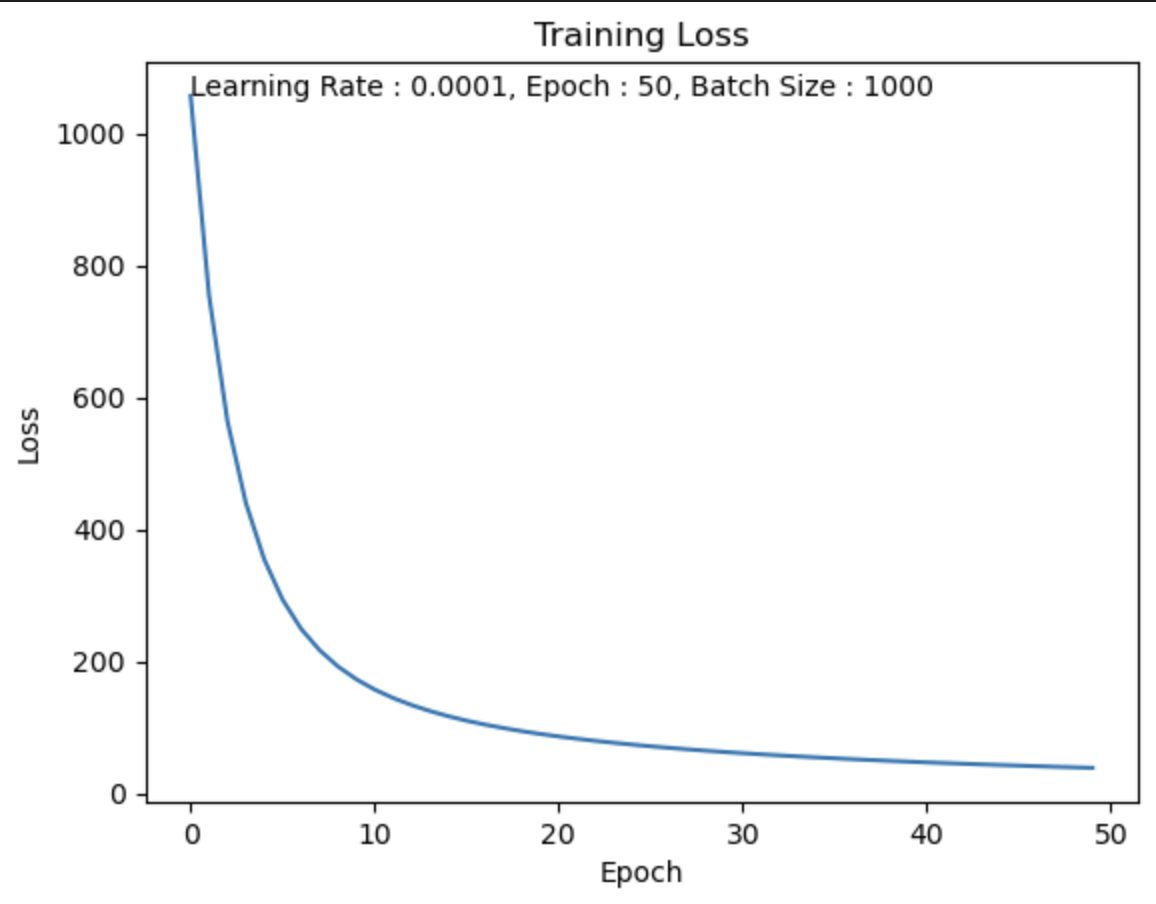
batch size를 1,000로 했을 때, 5분 26초.
Test Set의 데이터가 60,000개이고 batch size를 1,000로 했기 때문에
1 Epoch에 60번 반복을 수행한다.

Batch Size와 학습 시간의 관계

Train Data Set이 60,000개라고 가정하자.
만약 Batch Size를 1,000으로 설정했을 때, 한 Epoch 당 60번의 학습이 수행된다.
만약 Batch Size를 1로 설정했을 때, 한 Epoch 당 60,000번의 학습이 수행된다.
➡️ GPU를 사용한다고 가정했을 때,
batch size = 1이거나 batch size = 1000이거나
한 번의 학습을 수행하는 데는 똑같은 시간이 걸린다.
따라서 이러한 상황에서는 Epoch 당 학습 횟수를 줄이는 것이 더 빠를 것이다.
➡️ 따라서 Batch Size가 클수록 빠르다.

Batch Size와 학습 성능의 관계

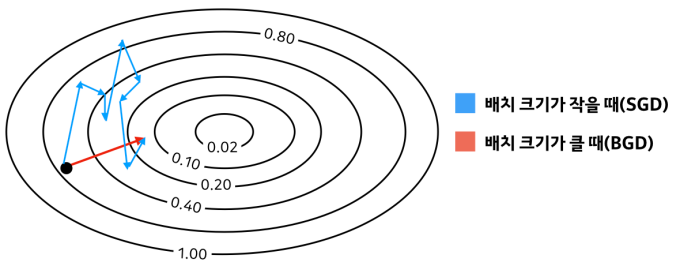
Batch Size가 클수록 빠르니까 Batch Size를 크게 하면 되지 않을까?
➡️ 안 된다.
- Batch Size가 크다는 것은 Train Set에서 많은 양을 data를 한 번에 볼 수 있다는 것을 의미한다.
  이 경우 학습을 하고 model의 weight를 update할 때, 최적화된 경로로 update하게 된다.
  Batch Size가 Train Set의 크기와 같다면, Batch의 분포와 Train 데이터의 분포가 같아진다는 의미가 된다.
  이렇게 된다면 Train 데이터의 분포만 따라가서 Overfitting으로 인해
  Test Set에 대한 Generalization이 떨어지게 된다.
- 또한 학습 도중에 Loss가 local optimal에 갇혔을 때는 더 이상 학습이 되지 않는다.
그러면 반대로 Batch Size를 작게 한다면?
- Batch Size가 극단적으로 작은 1이라고 가정하면,
  학습을 진행할 때, Batch에 Outlier가 포함되었을 때,
  실제 최적화된 경로가 아닌 다른 경로로 model의 weight가 update되어
  학습이 더디게 진행된다.
- 또한 local optimal에 빠지더라도
  Batch 내부의 특이값 혹은 그 자체의 분포가 실제 Train 데이터의 분포와 다르기 때문에
  Train 데이터의 최적화된 경로가 아닌 다른 경로로 움직여 local optimal에서 빠져나갈 수 있게 된다.

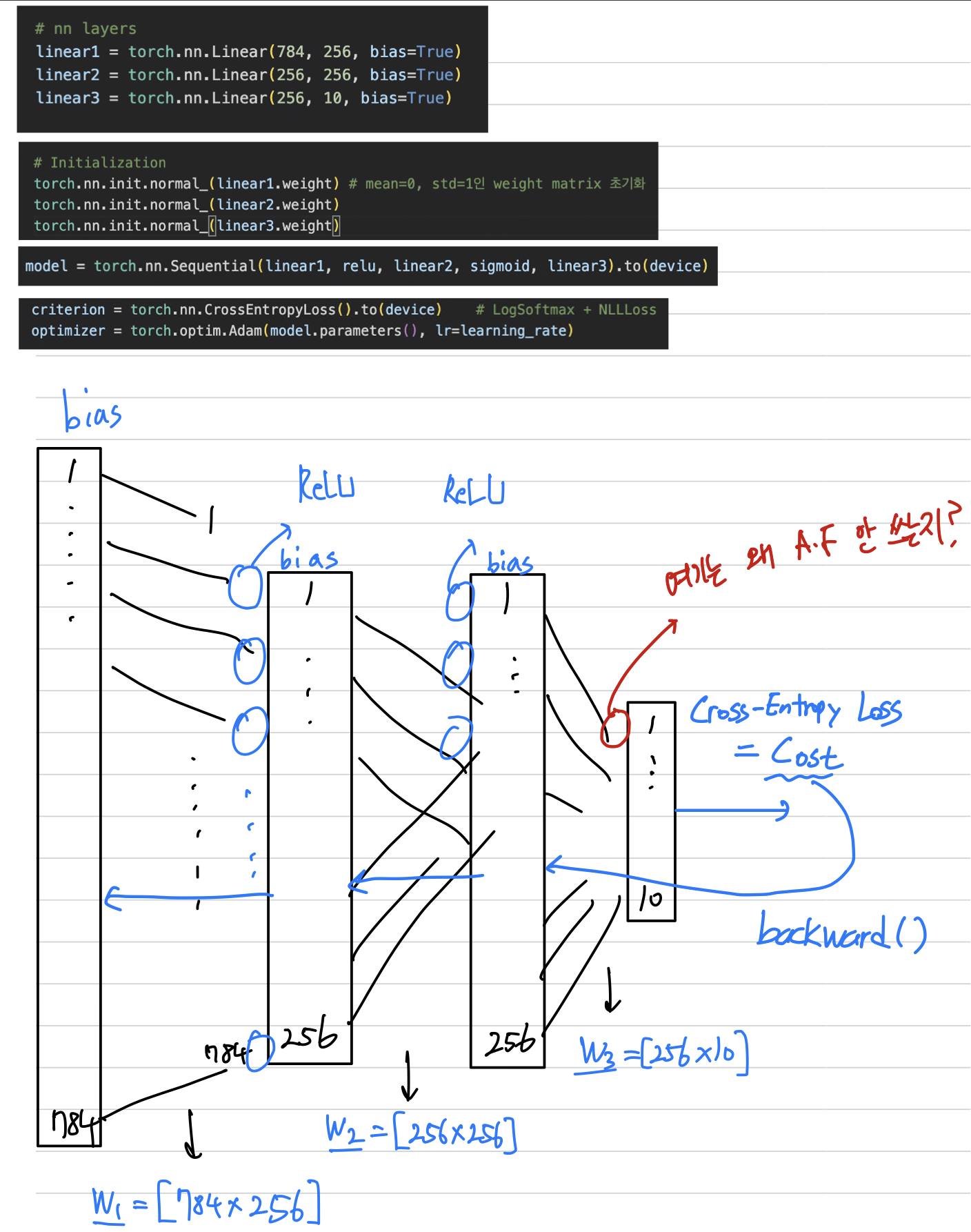
Hyper Parameter - Activation Function

sigmoid, sigmoid

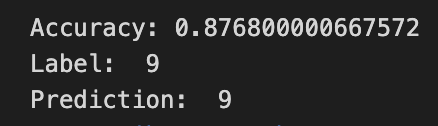
sigmoid, ReLU

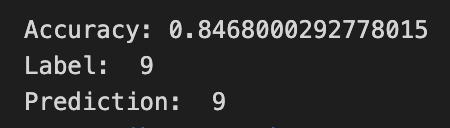
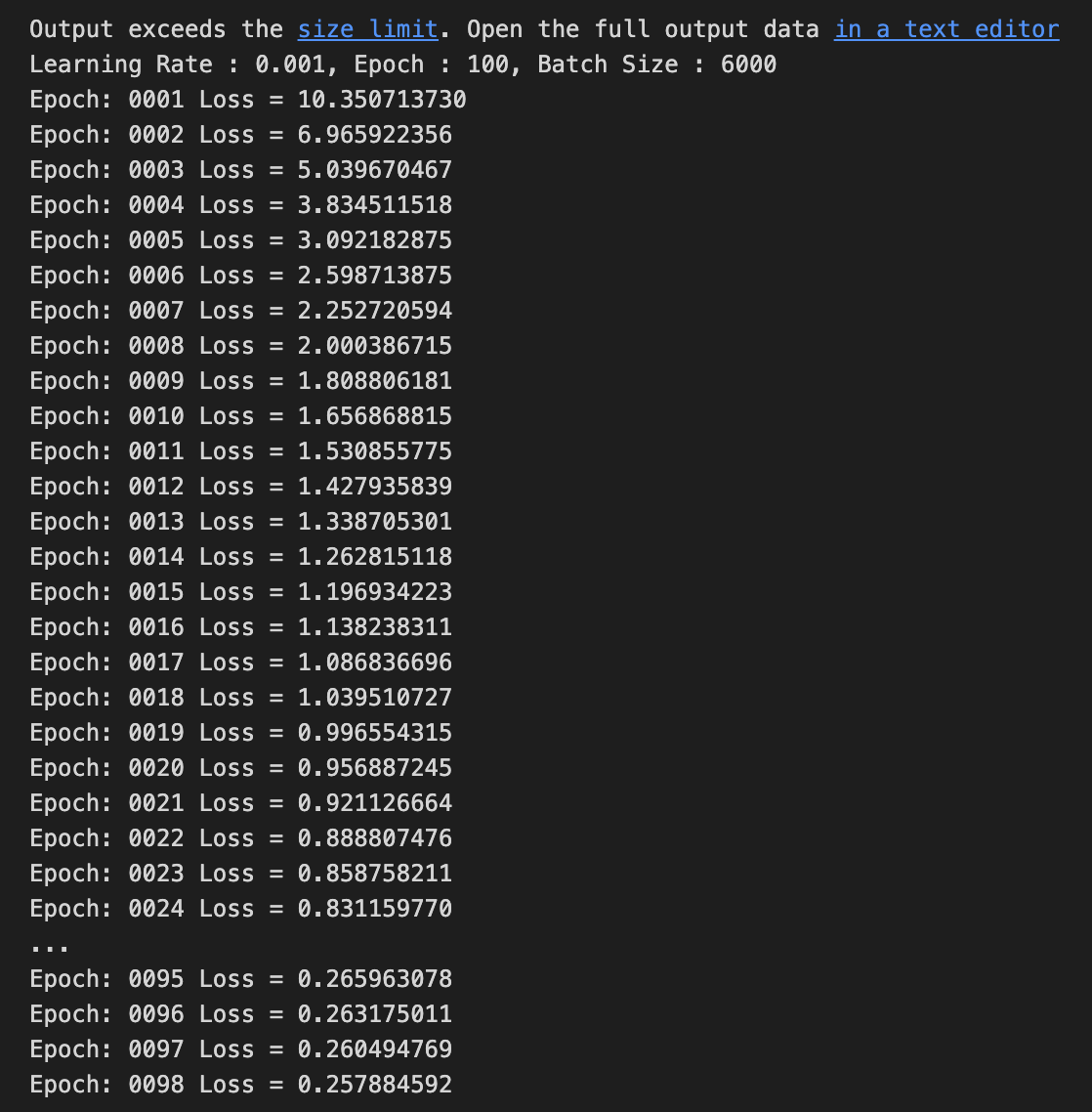
ReLU, sigmoid

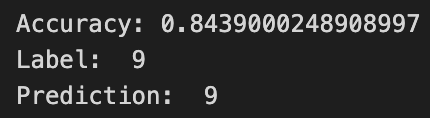
ReLU, ReLU

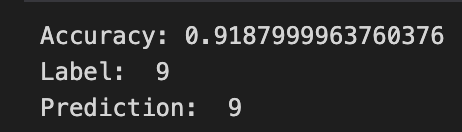
CNN, MNIST Classification

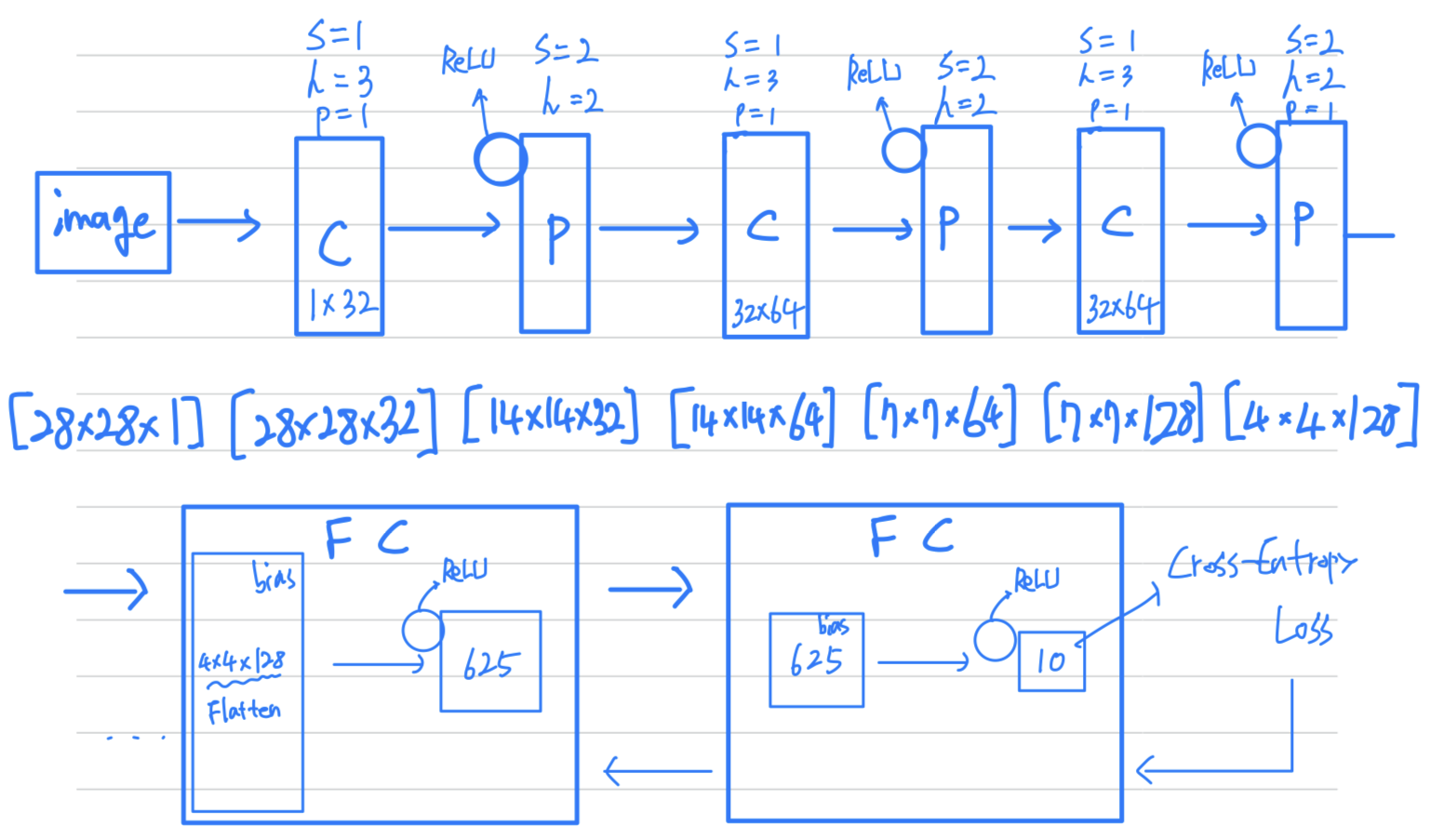
# CNN Model
class CNN(torch.nn.Module):

    def __init__(self):
        super(CNN, self).__init__()
        self.keep_prob = 0.5 # 남겨둘 뉴런 비율
        # L1 ImgIn shape=(?, 28, 28, 1)
        #    Conv     -> (?, 28, 28, 32)
        #    Pool     -> (?, 14, 14, 32)
        self.layer1 = torch.nn.Sequential(
            torch.nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(kernel_size=2, stride=2))
        # L2 ImgIn shape=(?, 14, 14, 32)
        #    Conv      ->(?, 14, 14, 64)
        #    Pool      ->(?, 7, 7, 64)
        self.layer2 = torch.nn.Sequential(
            torch.nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(kernel_size=2, stride=2))
        # L3 ImgIn shape=(?, 7, 7, 64)
        #    Conv      ->(?, 7, 7, 128)
        #    Pool      ->(?, 4, 4, 128)
        self.layer3 = torch.nn.Sequential(
            torch.nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(kernel_size=2, stride=2, padding=1))

        # L4 FC 4x4x128 inputs -> 625 outputs
        self.fc1 = torch.nn.Linear(4 * 4 * 128, 625, bias=True)
        torch.nn.init.xavier_uniform_(self.fc1.weight)
        self.layer4 = torch.nn.Sequential(
            self.fc1,
            torch.nn.ReLU(), 
            torch.nn.Dropout(p=1 - self.keep_prob)) #임의로 0으로 만들어 overfitting을 방지하는 역할을 합니다. p 인자는 드롭아웃할 뉴런의 비율을 나타냅니다. 1 - self.keep_prob은 남겨둘 뉴런의 비율을 나타냅니다. 
        # L5 Final FC 625 inputs -> 10 outputs
        self.fc2 = torch.nn.Linear(625, 10, bias=True)
        torch.nn.init.xavier_uniform_(self.fc2.weight)

    def forward(self, x):
        out = self.layer1(x)
        out = self.layer2(out)
        out = self.layer3(out)
        out = out.view(out.size(0), -1)   # Flatten them for FC
        out = self.layer4(out)
        out = self.fc2(out)
        return out

Hyper Parameter - stride

stride = 1

stride = 5

Hyper Parameter - filter size

filter size = 3

filter size = 10

Optimization 기법

학습을 순조롭게 진행되도록 하기 위해 Optimization 기법이 필요하다는 것을 느낌.
다음 Chapter가 학습을 위한 Optimization 방법이 나오는 것 같은데,
최적화를 공부해야 하는 이유를 알 수 있었다.

Hyungseop Lee

model compression

이전 포스트

[Chap 4] 딥러닝 기초

다음 포스트

[PyTorch 실습] MLP, CNN

[Study] Machine Learning

실습을 위한 사전지식

Softmax

Cross Entropy

optimizer

weight initialzation

torch.nn.init.normal_()

MLP, MNIST Classification

Hyper Parameter - Learning Rate

LR = 0.1

LR = 0.01

LR = 0.001

LR = 0.0001

한 눈에 살펴보고 분석하기

Hyper Parameter - Epoch

Epoch = 5

Epoch = 30

Epoch = 50

Epoch = 100

한 눈에 살펴보고 분석하기

Hyper Parameter - Batch Size

Batch Size = 10

Batch Size = 30

Batch Size = 100

Batch Size = 1000

Batch Size와 학습 시간의 관계

Batch Size와 학습 성능의 관계

Hyper Parameter - Activation Function

sigmoid, sigmoid

sigmoid, ReLU

ReLU, sigmoid

ReLU, ReLU

CNN, MNIST Classification

Hyper Parameter - stride

stride = 1

stride = 5

Hyper Parameter - filter size

filter size = 3

filter size = 10

Optimization 기법

[Chap 4] 딥러닝 기초

[Chap 5] 딥러닝 최적화

0개의 댓글

[Study] Machine Learning

`LR = 0.1`

`LR = 0.01`

`LR = 0.001`

`LR = 0.0001`