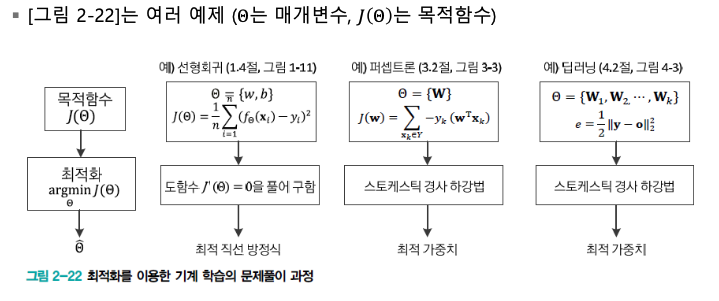
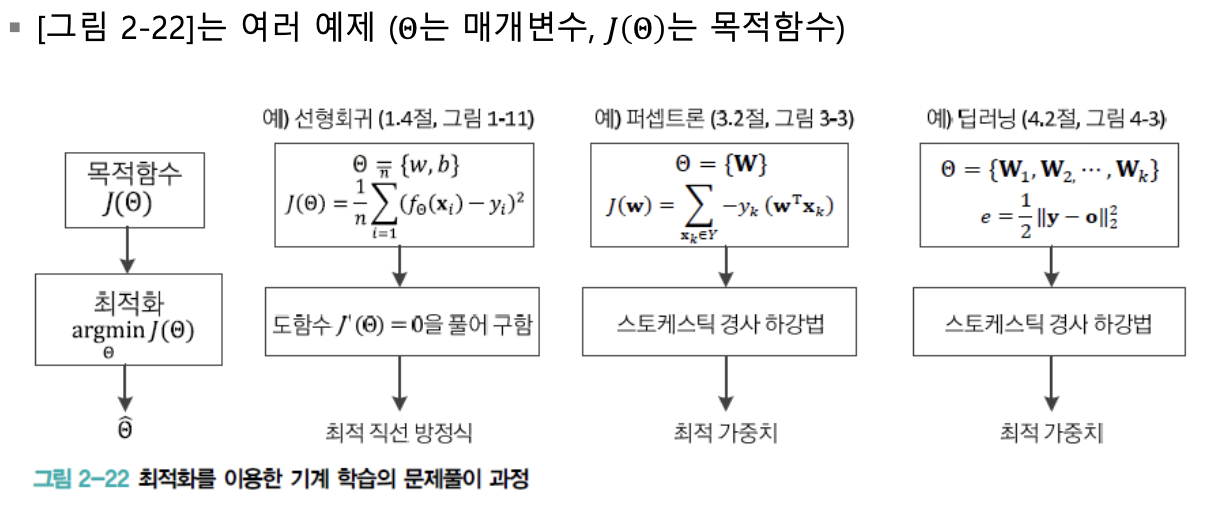
최적화
"기계학습은 최적화 과정이다." 라고 말해도 될 정도로
기계학습은 최적화를 많이 사용한다.
주어진 데이터를 가지고 최적화 문제를 어떻게 공식화할 것인가,
최적화 공식을 어떻게 풀어 최적의 해, 즉 목적함수를 최소로 하는 점을 찾은 것인가가 기계학습의 핵심 주제이다.
기계학습에서의 최적화는 순수 수학에서와 달리,
잡음이 심한 열악한 데이터를 잘 이용하여 미분을 계산하는 과정이 매우 중요하다.
이 절에서는 기계 학습이 가장 널리 사용하는,
데이터로 미분을 계산하면서 최저점을 찾아가는 경사하강법(Stocatic Gradient Descent, SGD)를 공부한다.
매개변수 공간의 탐색
학습 모델의 매개변수 공간
-
훈련집합은 아주 높은 차원에 정의된 매우 희소한 데이터에 불과하고
이런 데이터를 가지고 참인 확률분포를 구하는 일은 불가능하다. -
이러한 이유 때문에 기계 학습은 적절한 모델을 선택하고 목적함수를 정의하며,
모델의 매개변수 공간을 탐색하여 목적함수가 최저가 되는 최적점을 찾아내는 전략을 사용한다.
➡️ '특징 공간에서 해야 하는 일을 모델의 매개변수 공간에서 하는 일로 대치'한 셈이다.
-
모델의 매개변수 공간은 특징 공간보다 수 배 ~ 수만 배 넓다.
예를들어, Iris data를 인식하기 위한 퍼셉트론의 경우 특징 공간은 4차원이지만,
매개변수는 총 12개로 매개변수 공간은 12차원이다.
최적해
- 다음은 각각 1차원, 2차원의 가상의 목적함수이다.
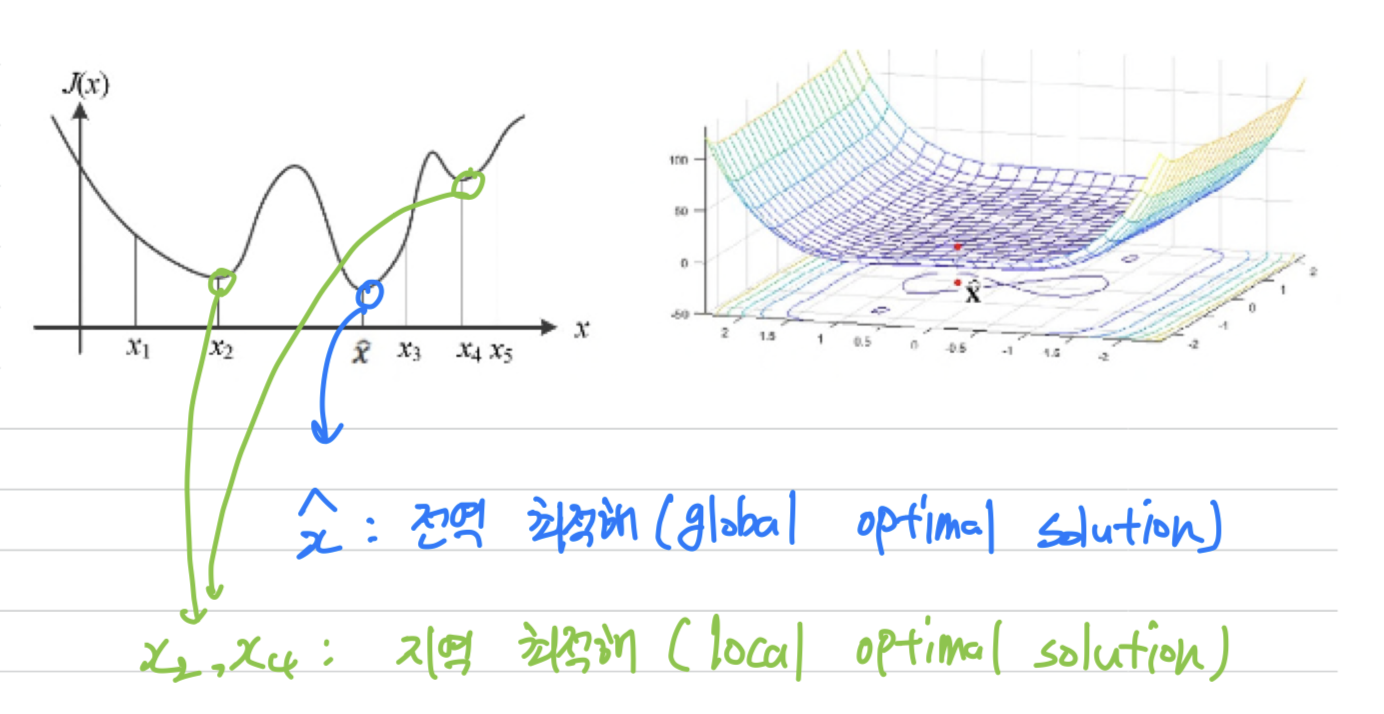
- : 전역 최적해(global optimal solution)
- : 지역 최적해(local optimal solution)
➡️ 와 같이전역 최적해에 가까운 지역 최적해를 찾고 만족하는 경우가 많다.
하지만 진정한 전역 최적해가 아니므로 그렇게 되면 안 된다.
기계 학습 알고리즘이 해야 할 일
목적함수 를 최소로하는 최적해 를 찾는 것.
즉, =
최적화 문제해결
- 다음 알고리즘은 기계학습에서 사용하는 전형적인 알고리즘이다.

- line 3 : 목적함수가 작아지는 방향을 찾는 가장 확실한 방법은
미분이다.
미분은 함수의 기울기를 알려주는데,
기울기는 함숫값이 작아지는 방향이므로 로 사용할 수 있다. - line 5 : 현실에서 목적함수가 0.0에 근접하지 않은 상태로 수렴하는 경우가 있어서,
반복을 멈추기 위해멈춤 조건으로 정의.
- line 3 : 목적함수가 작아지는 방향을 찾는 가장 확실한 방법은
미분
미분의 정의
미분이란,
어떤 점에서의 기울기, 즉 가 미세하게 증가하였을 때 함수값의 변화율을 알려준다.
-
함수 의 1차 미분 == 함수 의 1차 도함수 == 는 다음과 같이 정의한다.
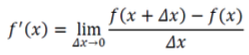
-
함수 의 2차 미분 == 함수 의 2차 도함수 == 는 다음과 같이 정의한다.
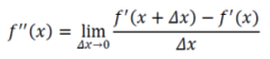
경사하강법의 핵심 원리
-
- 방향으로 가면 최저점을 만난다. (이는 경사 하강법의 핵심 원리이다)
➡️ = 이다.
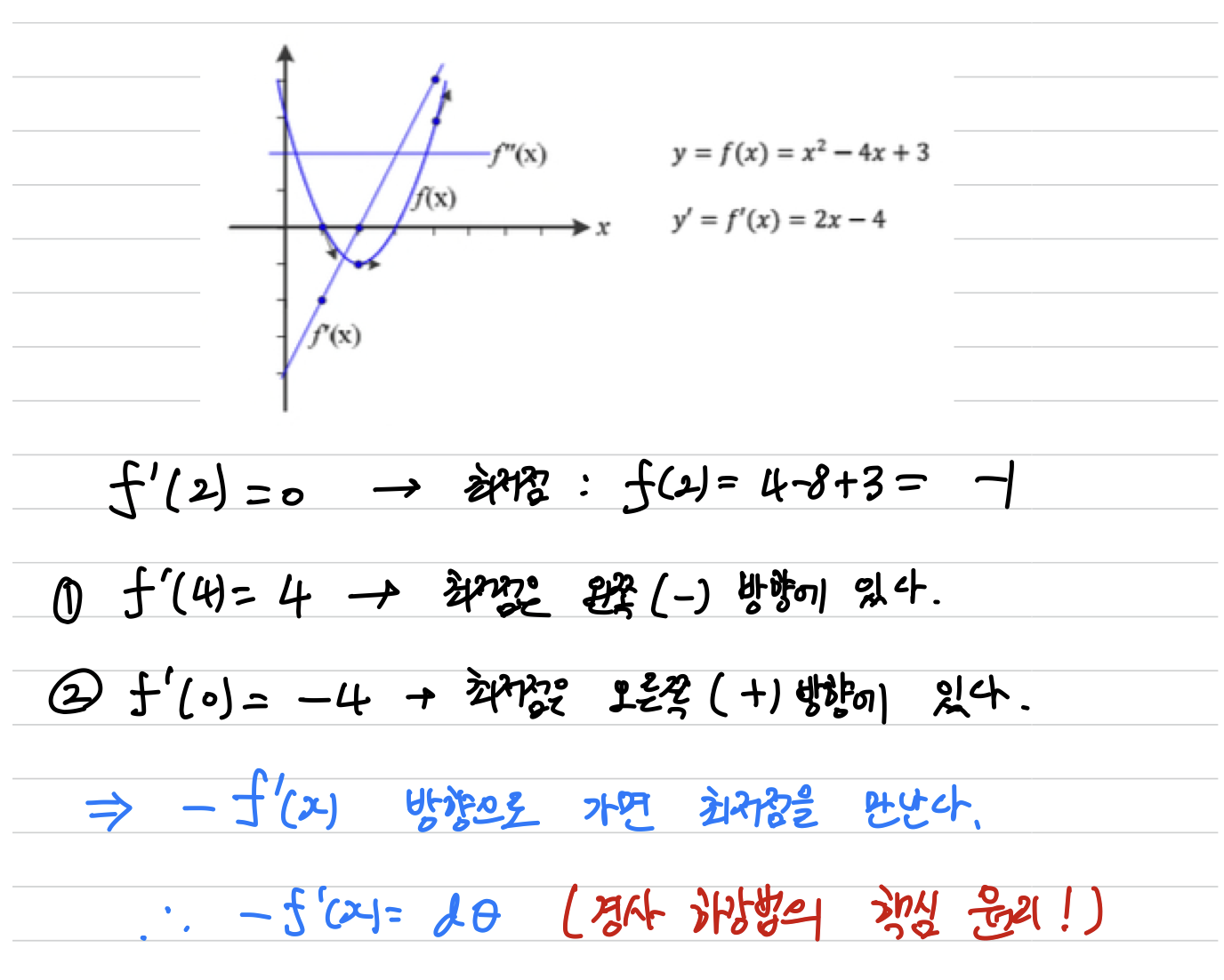
- 여기서의 예시는 특수 상황이 아닌 일반적으로 성립하는 정리이다.
-
따라서 <##최적화 문제해결> 에서의 그림을 다음과 같이 나타낼 수 있다.

분석적 방법 vs 수치적 방법
-
분석적 방법: 고등학교 수학에서 을 풀면 최저점을 구할 수 있다는 사실을 배웠다.
이와 같이 수식을 풀어 최저점을 찾는 방법을 분석적 방법이라고 한다. -
수치적 방법: 만큼 조금씩 이동하는 일을 반복하여 최저점을 찾는 접근방법을 수치적 방법이라고 한다.
분석적 방법은 차원이 낮고 목적함수가 단순한 경우에 적용할 수 있는데,
기계학습은 이러한 조건을 벗어나므로 수치적 방법을 사용한다.
편미분
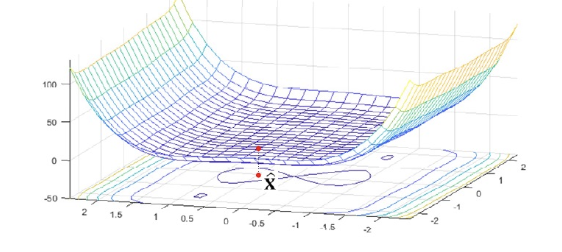
- 아래의 그래프는 다음의 식으로 정의되는 함수이다.
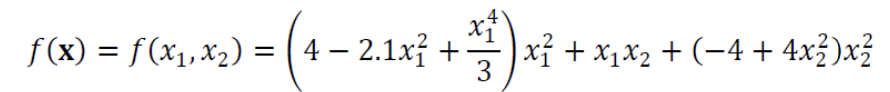
-
2개의 변수 로 함수가 정의되므로, 1차 도함수도 2차원이다.
이러한 미분을편미분(Partial Differentiation)이라고 한다.편미분은 변수 각각에 대해 독립적으로 미분하면 된다.
편미분의 결과는 Vector 형태가 되는데, 이 벡터를Gradient라고 한다.
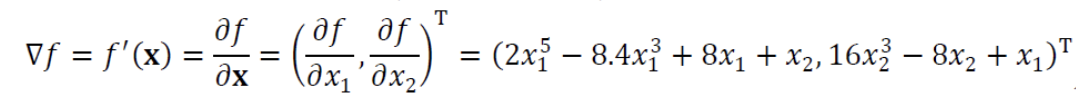
-
편미분을 이용하여 다차원 공간에서의 최저점을 찾을 수 있다.
독립변수와 종속변수의 구분
-
기계학습에서는 높은 차원에 비해 훈련집합의 크기가 작아 참인 확률분포를 구하는 일은 불가능하다.
따라서 기계 학습은- 적절한 모델을 선택하고,
- 목적함수를 정의하고,
- 모델의 매개변수 공간을 탐색하여 목적함수가 최저가 되는 최적점을 찾는 전략 사용.
➡️ 특징 공간에서 해야 하는 일을 모델의 매개변수 공간에서 하는 일로 대치한 셈

-
연쇄법칙
-
연쇄법칙(Chain Rule)을 이용하여합성함수의 도함수를 구할 수 있다. -
합성함수 가 있을 때, 도함수 는 다음과 같다.
➡️ -
합성함수 가 있을 때, 도함수 는 다음과 같다.
➡️ -
example
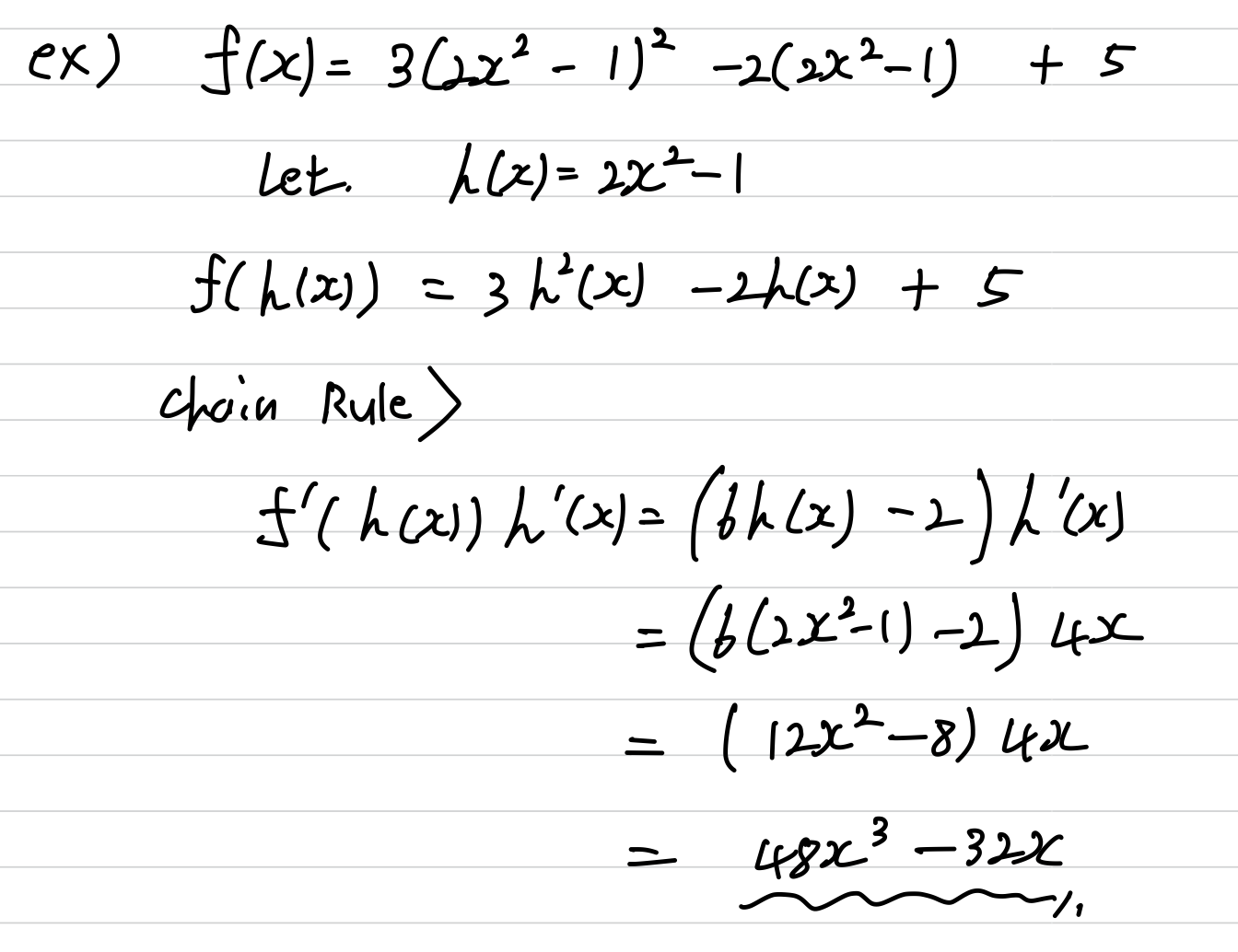
연쇄법칙을 알아야 하는 이유
- 다음과 같이, 다층 퍼셉트론은 합성함수로 되어 있다.(연쇄법칙이 적용된다)
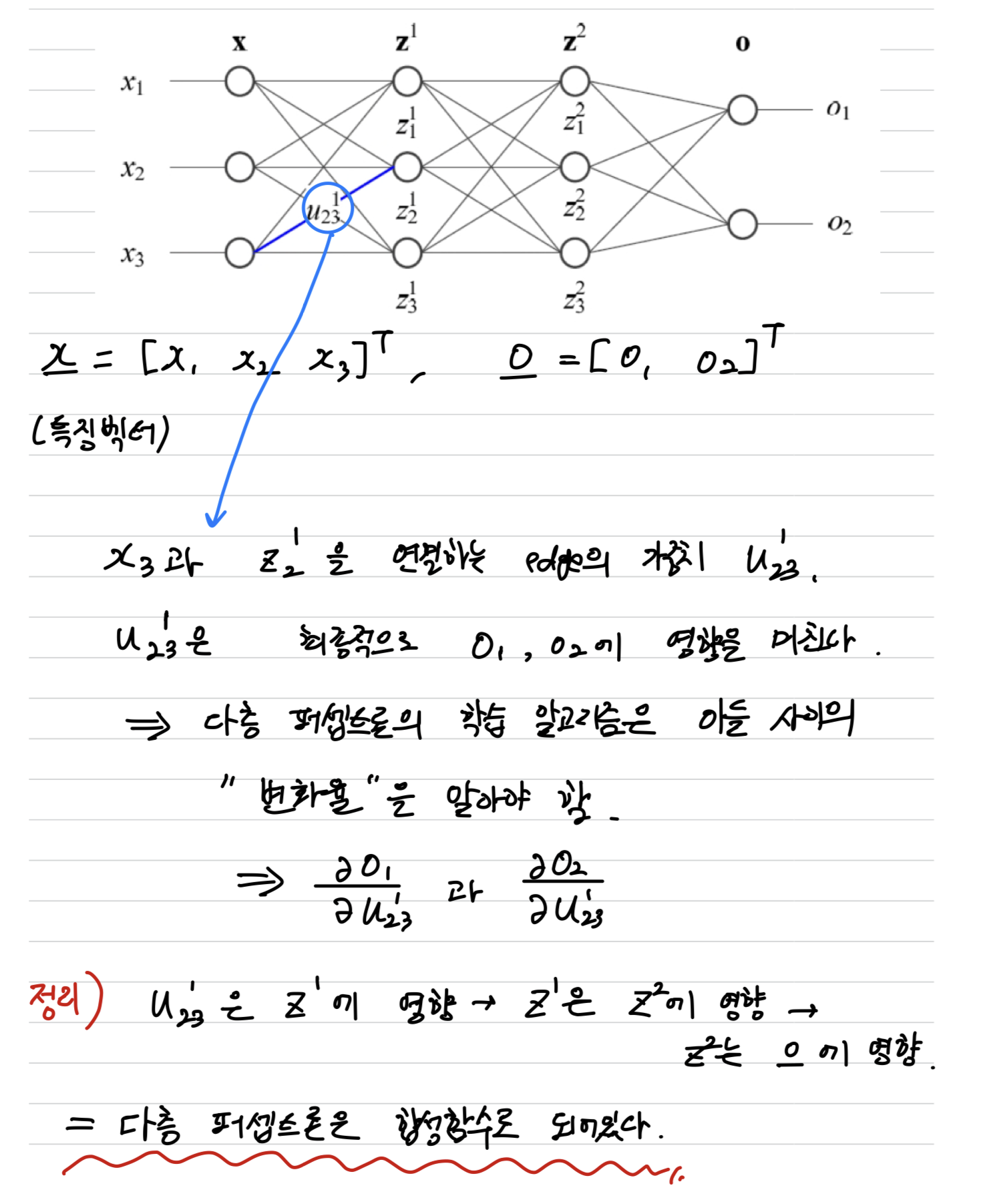
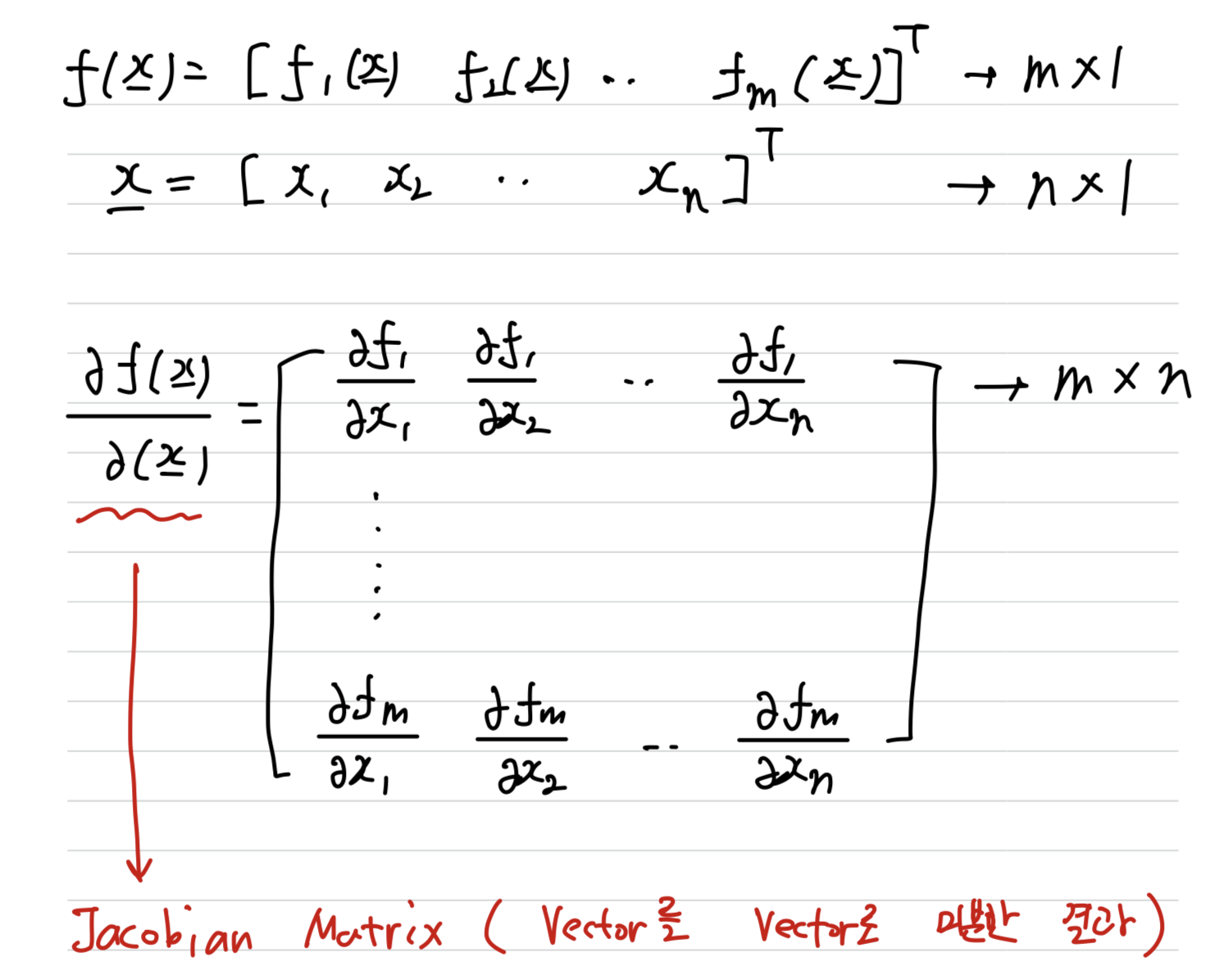
Jacobian Matrix(자코비안 행렬)
출력값이 [m * 1]인 다변수 함수 vector 의
[n * 1]인 입력 변수 vector 에 대한 편미분을 계산한 결과 나온,
[m * n] Matrix를Jacobian Matrix라고 한다.
- example
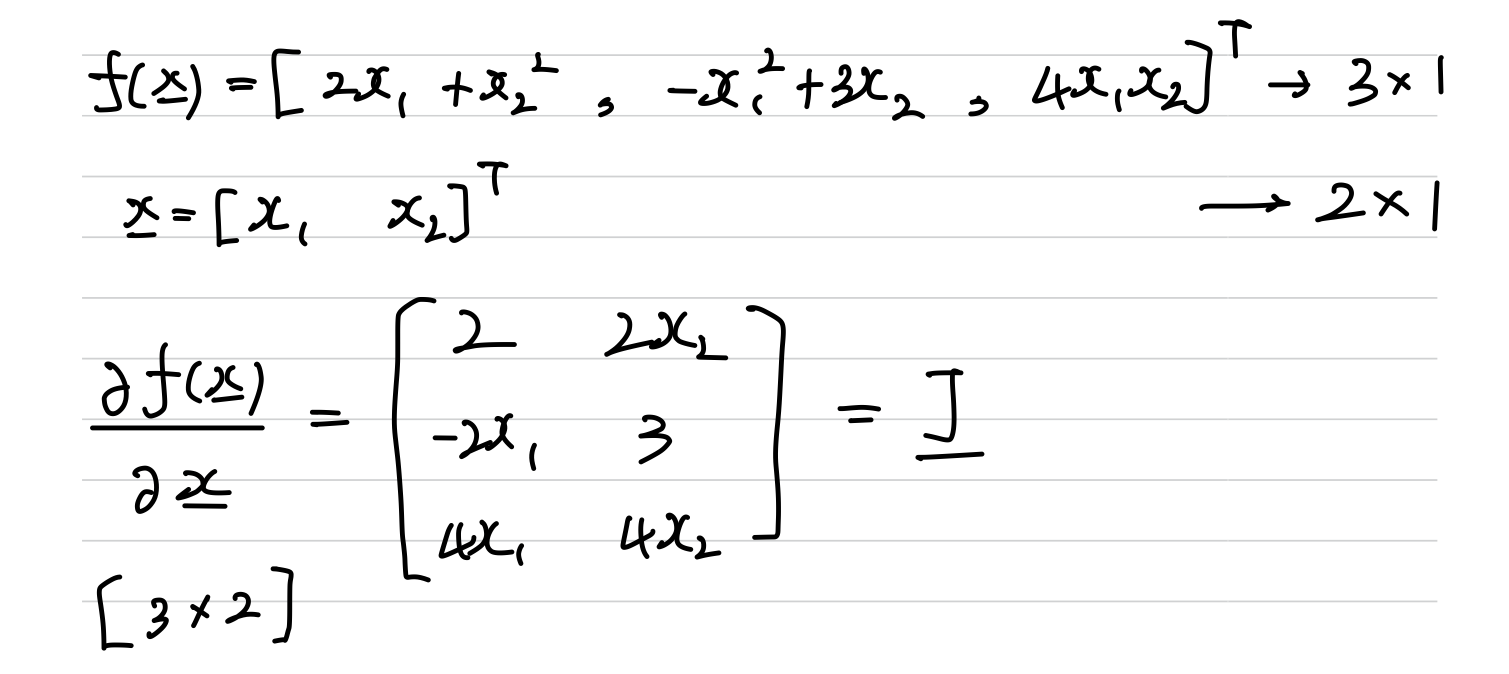
Hessian Matrix(헤시안 행렬)
다변수 함수인 의
[n * 1]인 입력 변수 vector 에 대한이차 편미분을 계산한 결과 나온,
[n * n] Matrix를Hessian Matrix라고 한다.
- example

Taylor Series(테일러 급수)
-
함수 자체를 모른는 상황에서,
어떤 점 에서의 함숫값 와 미분 가 주어지고,
이웃한 점()에서의 함숫값을 추정해야 하는 상황이 있다.
➡️ Taylor Series는 이 문제를 해결해 준다.- : 로부터 만큼 떨어져 있는 이웃점
- 값이 작을수록 추정값은 정확하다.
-
Taylor Series는 다음과 같이 정의할 수 있다.

- example

- example
경사 하강 알고리즘
앞서 미분으로 알아낸 Gradient의 반대 방향으로 가야
최적해에 도달 할 수 있다는 것을 알 수 있었다.
- 라고 표기
- gradient의 방향은 알 수 있지만, 얼마만큼 이동해야 최적해에 도달하는지는 알 수 없으므로
이동량을 조절하기 위해 Learning Rate(학습률)을 사용한다.
Learning Rate == 라고 표기.
(보통 보수적으로 조금씩 이동하기 위해 1보다 훨씬 작은 값을 학습률로 사용.)
다음과 같은 식을 이용하는 최적화 알고리즘을
경사 하강법(Gradient Descent Method)라고 한다.
: Learning Rate
: Gradient
BGD(Batch Gradient Descent)
BGD는 모든 샘플의 Gradient를 평균한 후 한꺼번에 매개변수를 갱신한다.
따라서 batch(배치)라는 단어가 있는 것이다.

- 현대 기계학습은 BGD을 거의 사용하지 않고, 대신 SGD를 사용한다.
SGD(Stochastic Gradient Descent)
SGD알고리즘은 한 번에 샘플 하나의 Gradient를 계산하고 즉시 매개변수를 갱신한다.
이러한 일을 모든 샘플에 수행하면한 세대(epoch)가 지났다고 말한다.
알고리즘은 멈춤 조건이 만족될 때까지 epoch을 반복한다.
새로운 epoch이 시작할 때마다 샘플의 순서를 섞어 알고리즘의 임의성을 투입한다.
이 임의성 때문에 Stochastic이라는 단어가 있는 것이다.