Image Sampling and Quantization

Type of images

• binary image : 0 or 1, 8bit에서는 0 or 255
  

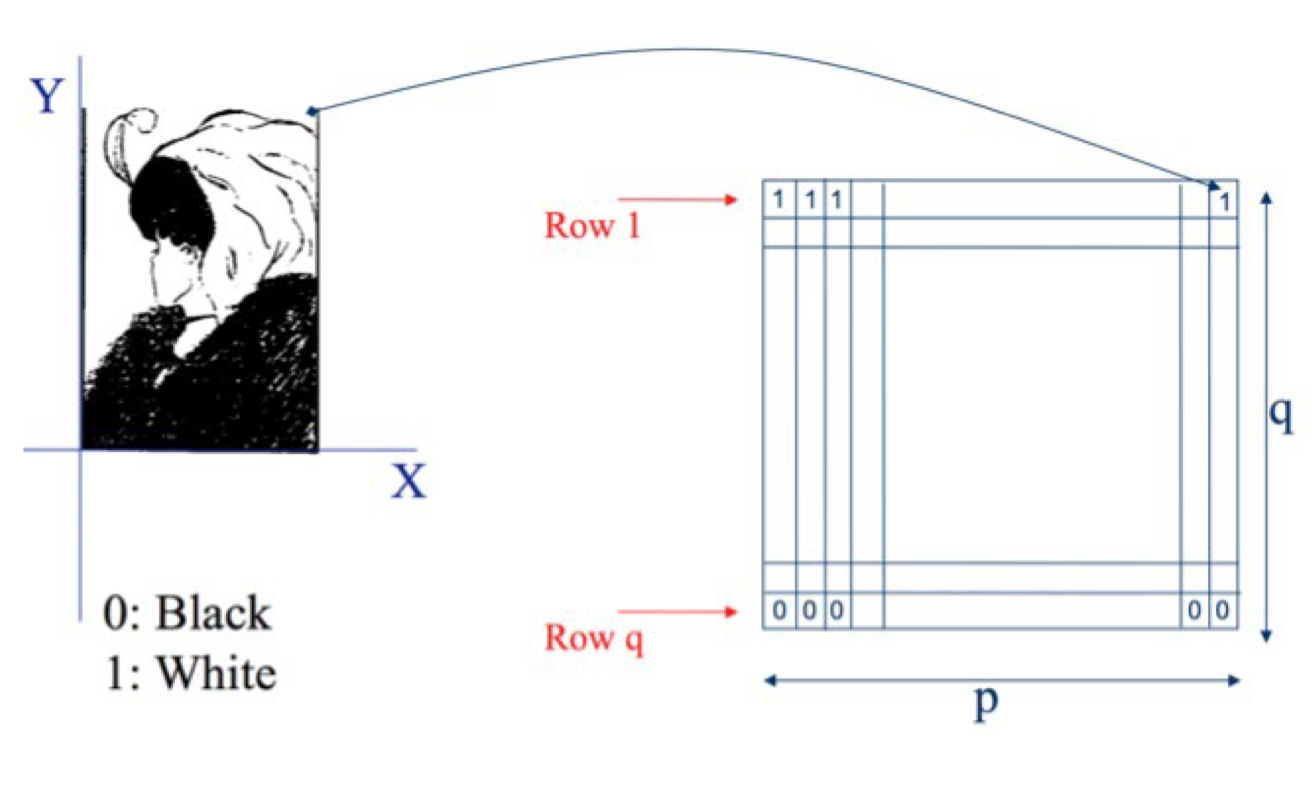
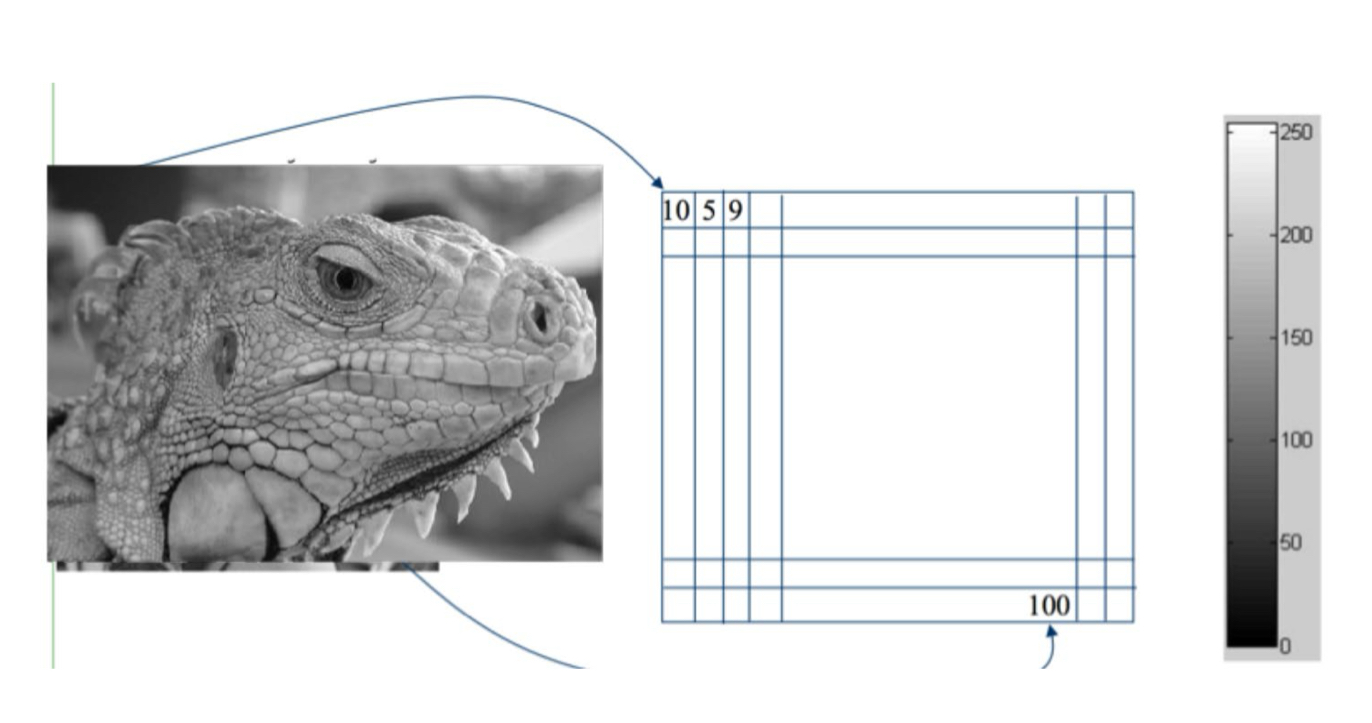
• gray scale image : [0, 255]
  

• color image : [0, 255] * 3
  

Resolution

• a sampling parameter, defined in dots per inch(DPI) or pixels per inch(PPI)
  • DPI or PPI가 높으면? resolution이 높다고 말함.
  • DPI or PPI가 높으면? sharp and clear한 image.
• Images are sampled and quantized.
  An image contains discrete number of pixels.
  • pixel value :
    • if gray scale, [0, 255]
    • if color scale, [R, G, B]

---

Image Histogram

• Historgram : image의 brightness(intensity)에 대한 frequency(빈도)를 시각화
  

---

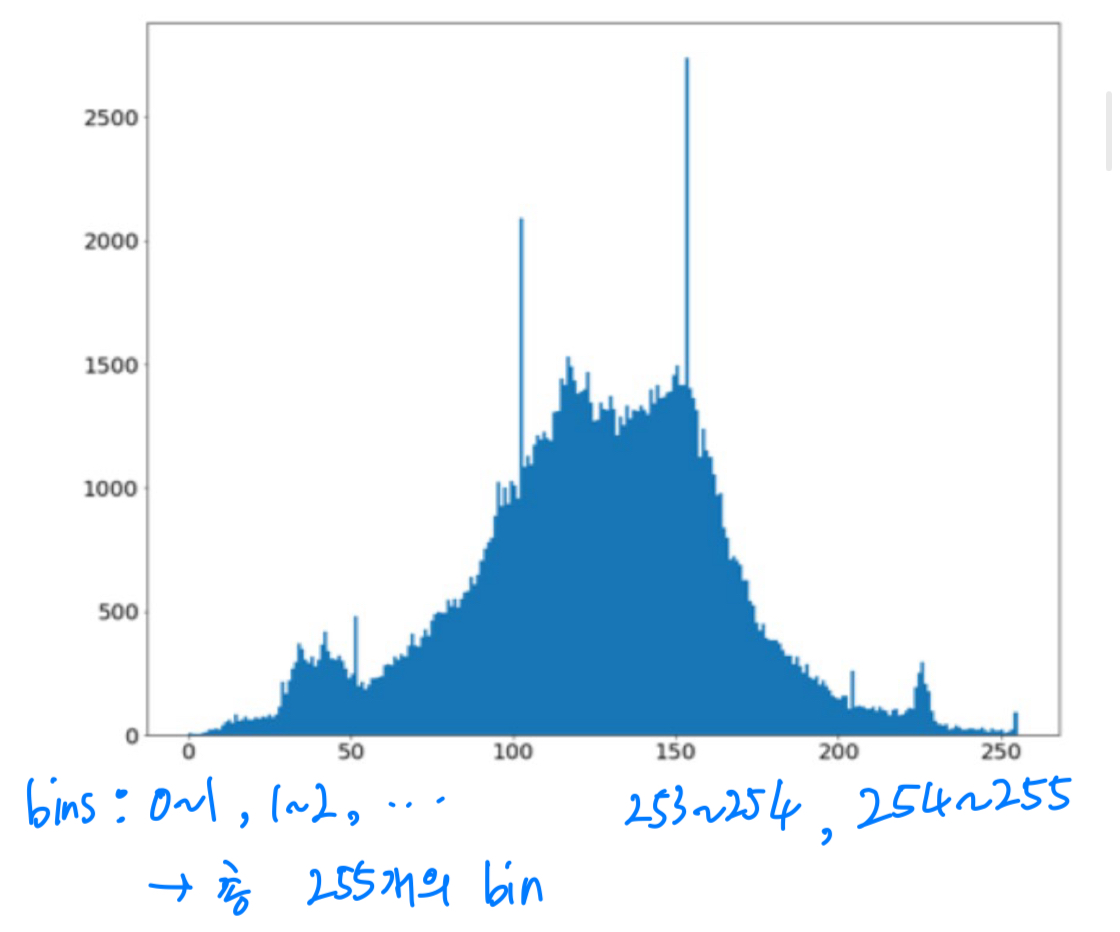
Image as functions

• image를 좌표공간으로서 나타낼 수 있다.
  an image as a function $f$ from $R^2$ to $R^m$ ($m$ = [0, 255])
  $f(x, y)$ gives the intensity at position $(x,y)$
  

---

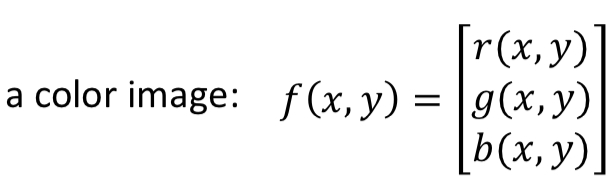
Linear systems (=filters)

• image filtering이란? :
  image를 원하는 방향으로 transformation하기 위해 다양한 operation을 적용해야 하는데,
  이를 위해서 image에 filter = kernel을 적용한다.

• filter 사용 목적 :

  1. features(edges, corners, blobs, ...)
  2. De-nosing (salt and pepper noise, ...)
  3. Super-resolution (resolution 향상)
  4. In-painting (주변 pixel의 context에 기초하여 자동으로 pixel 채워줌)

• System = Filter :
  converts an input(image의 특정 pixel) $f[n, m]$ into an output(=response) $g[n, m]$
  

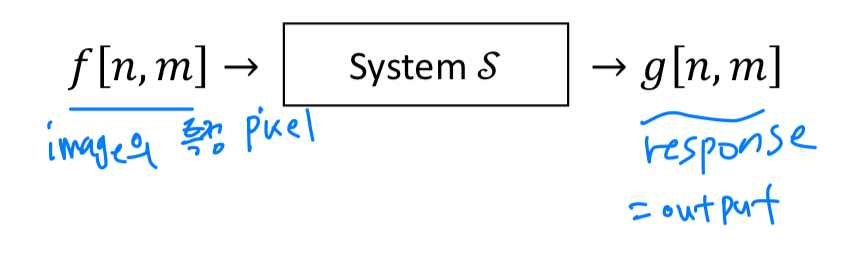
• S is the system operator :
  

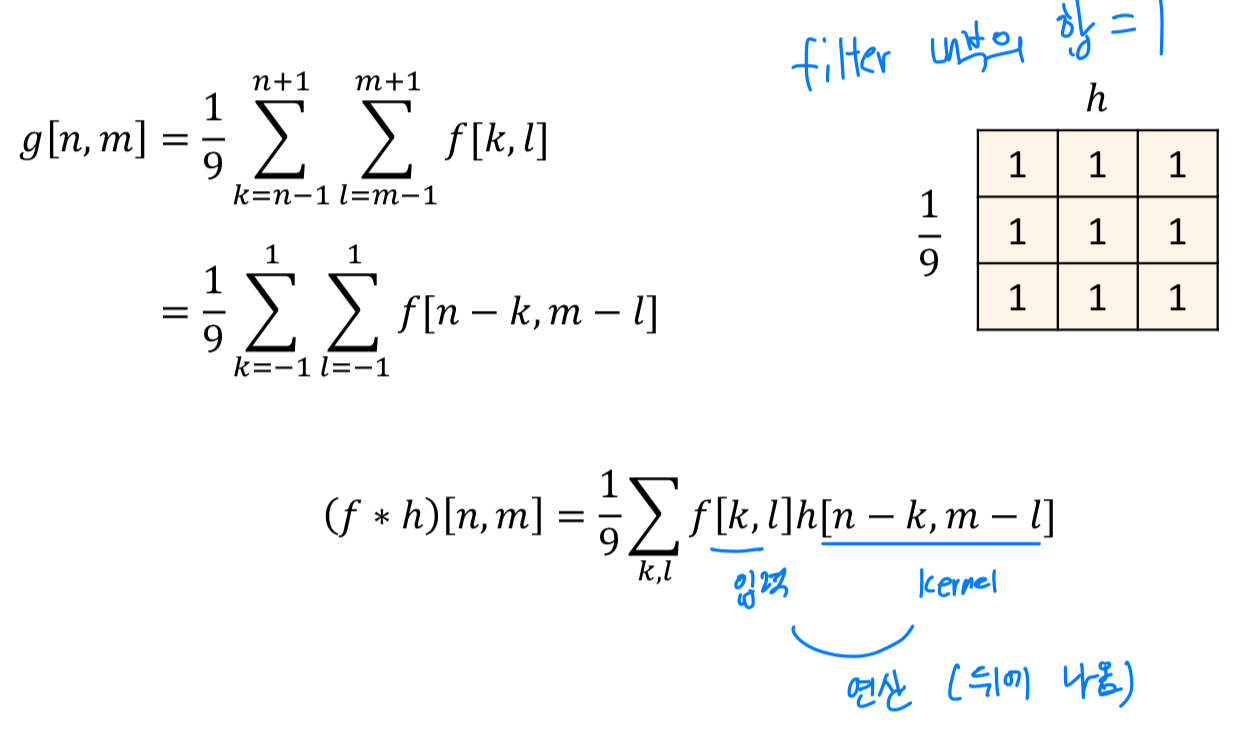
Ex1 : Moving average

• moving average filter : blur하게 만드는 효과 = smoothing effect = remove shart features
  

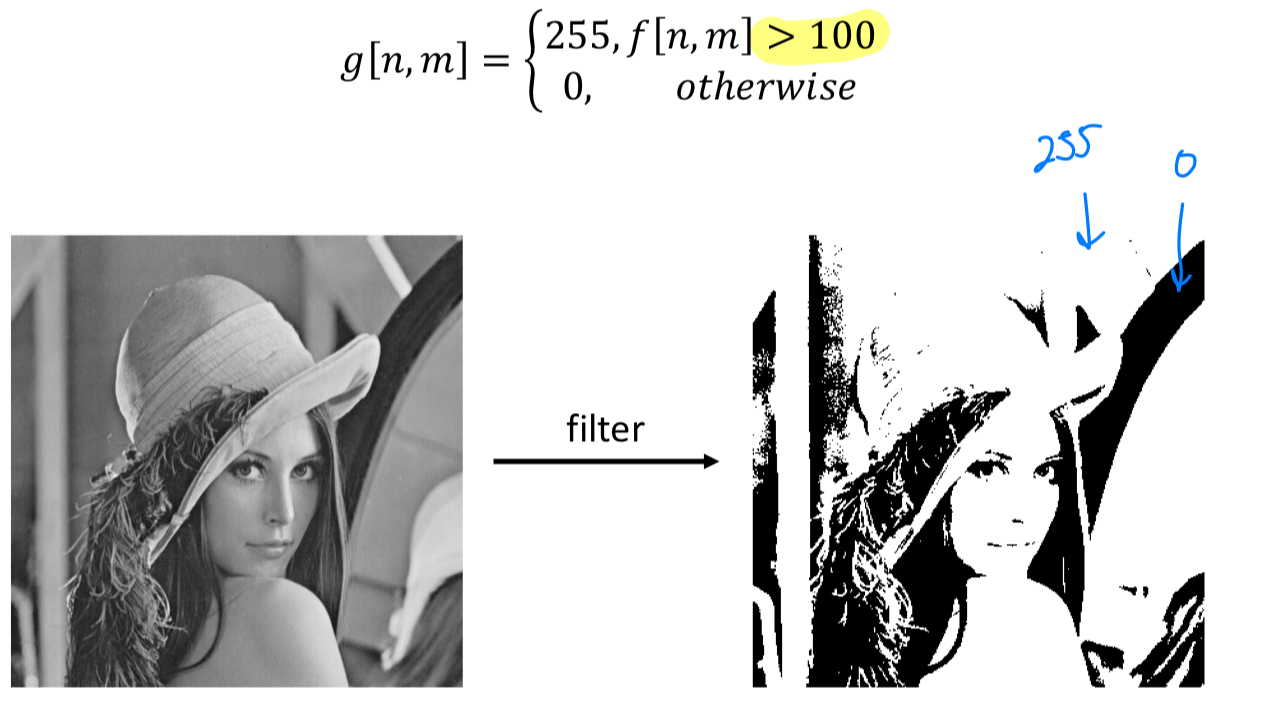
Ex2 : Image segmentation

• Image segmentation : 특정 threshold 이하이면 0, 아니면 255
  

---

amplitude properties of systems

• Filter의 여러 속성들
  

---

Linear system(filters)

• Linear system = filter :
  superposition 속성을 만족하는 것을 Linear system이라고 한다.
  

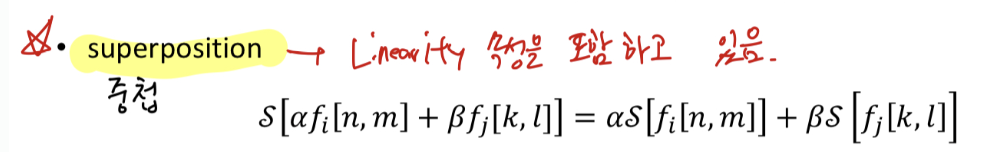
• moving average는 linear system인가?
  = moving average가 superposition 속성을 만족하는가?
  

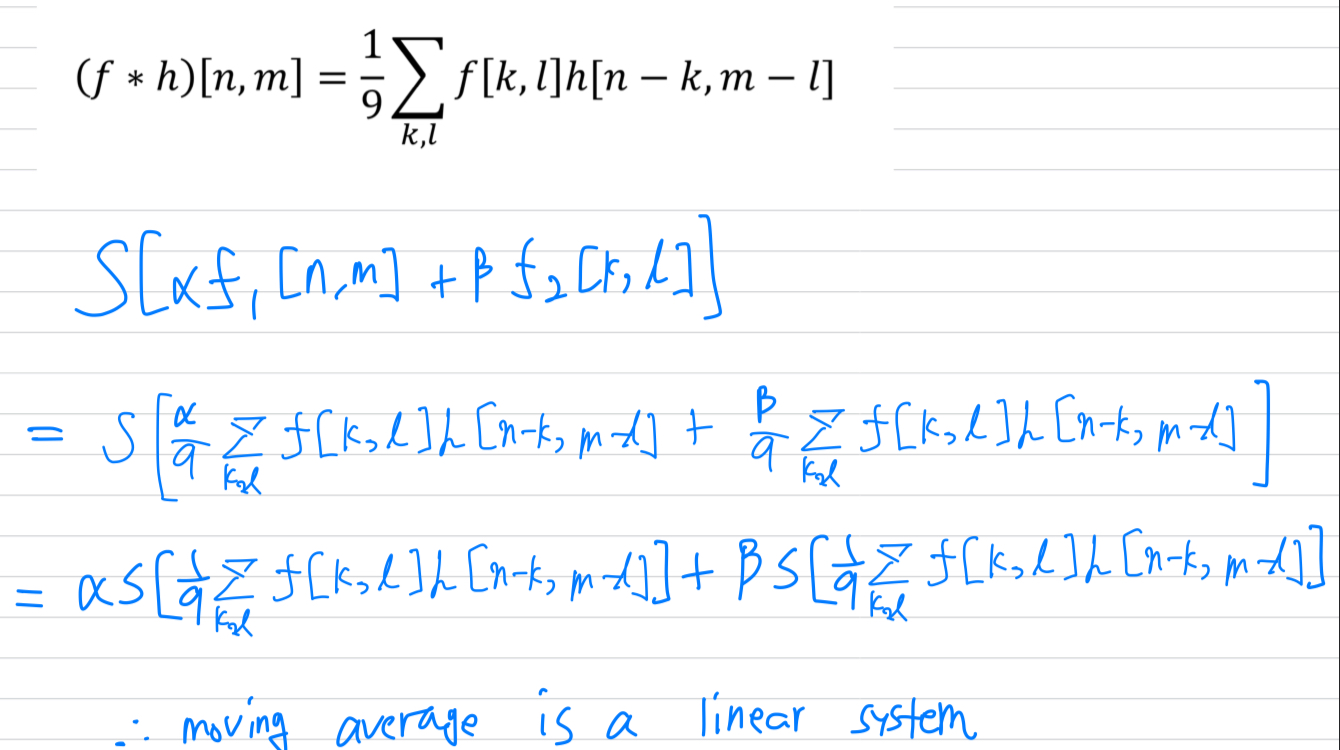
Linear Shift Invariant systems (LSI systems)

• LSI system :
  Superposition과 Shift invariance 속성을 모두 만족하는 것을 LSI system이라고 한다.

• 우리는 $f[n, m]$로부터 $g[n, m]$를 어떻게 계산할 것인가?
  

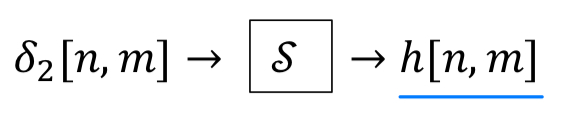
• 만약 linear system $S$가 무슨 일을 하는지 모른다면,
  impulse function(=Dirac delta function) $\delta_2()$을 Linear system $S$에 넣어
  impulse response $h[n, m]$을 얻어낸다.
  $h[n, m]$은 Linear System의 내부가 어떻게 동작하는지 알 수 있는 impulse function에 대한 response이다.

• 그런데 impulse response $h[n, m]$으로 우리는 어떻게 $f[n, m]$로부터 $g[n, m]$를 어떻게 계산할 것인가?

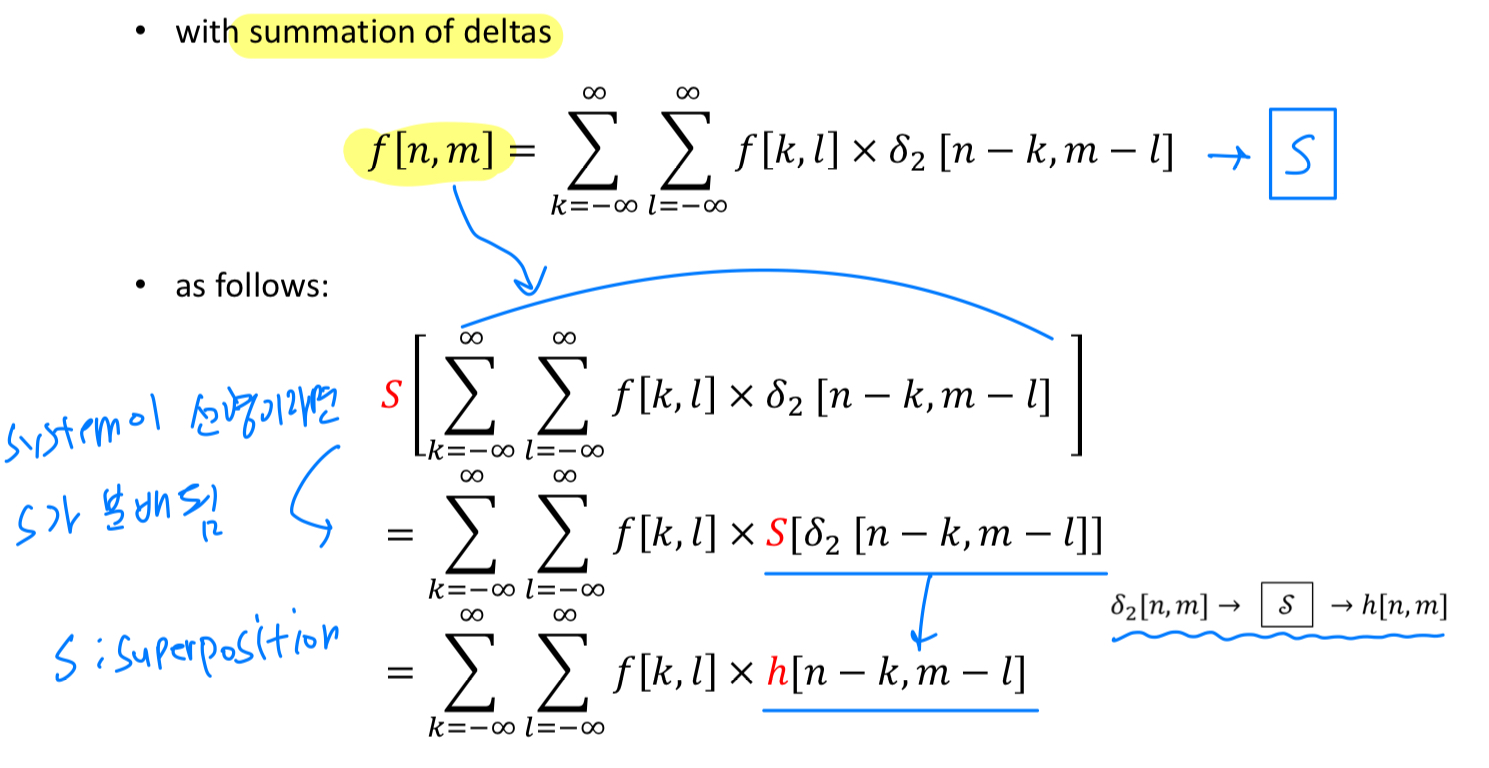
• General LSI system에서는 :
  주어진 image $f[n, m]$을 impulse resonse로 쪼개어 Linear System이 어떤 일을 하는지 간접적으로 확인할 수 있다.
  

General LSI system

• General LSI system에서 우리는 3가지 properties가 필요하다.
  1. delta function을 LSI system $S$에 넣은 impulse reponse를 알고 있다.
     
  2. LSI system은 shift invariance 속성을 만족한다.
     
  3. LSI system은 superposition 속성을 만족한다.
     

impulse response가 shift invariance하고 superposition하다면, LSI system을 거쳤다고 말할 수 있다.

• We can generalize superposition principle
  

---

2D convolution (*)

• 

Example

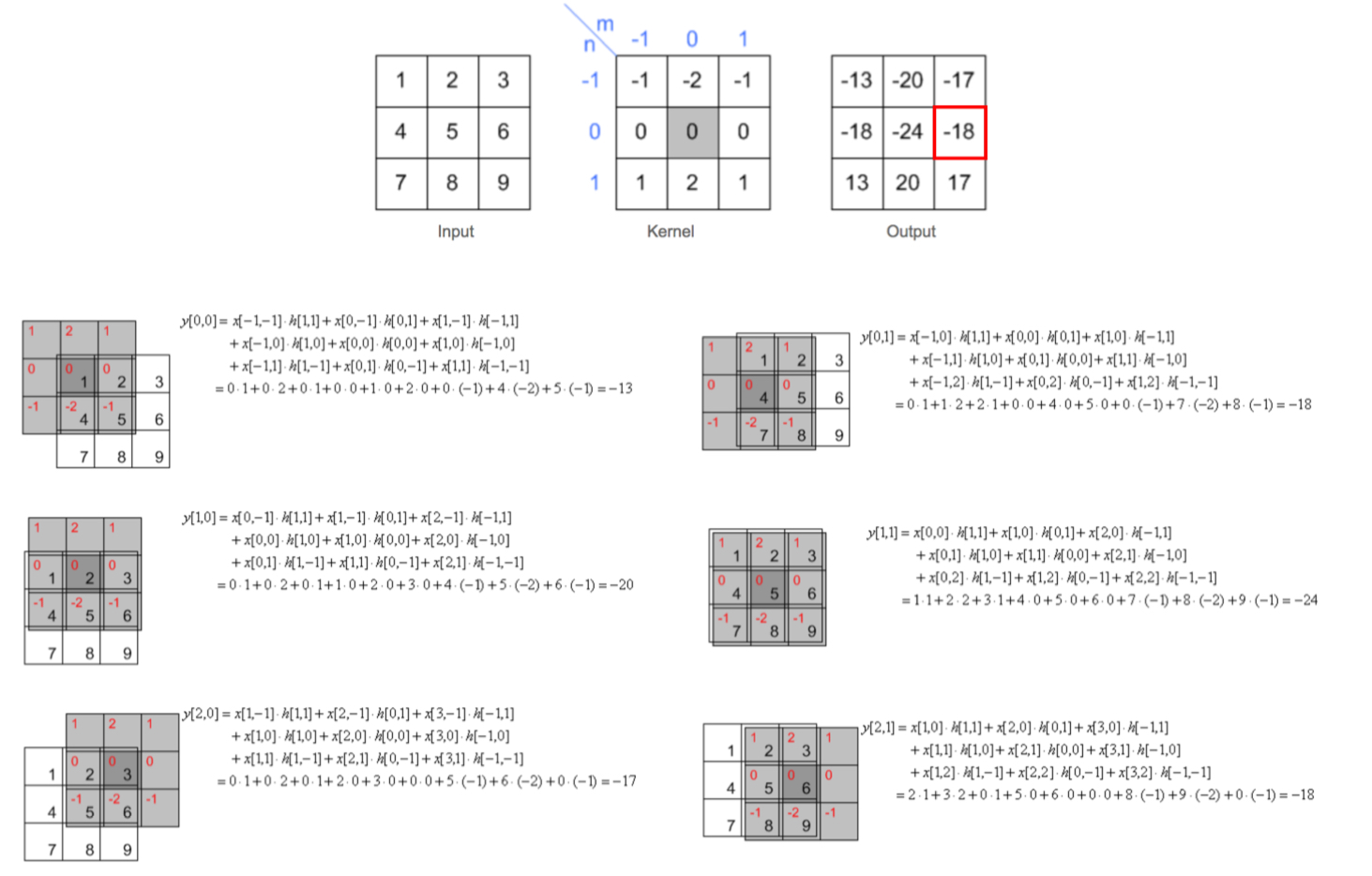
identity kernel

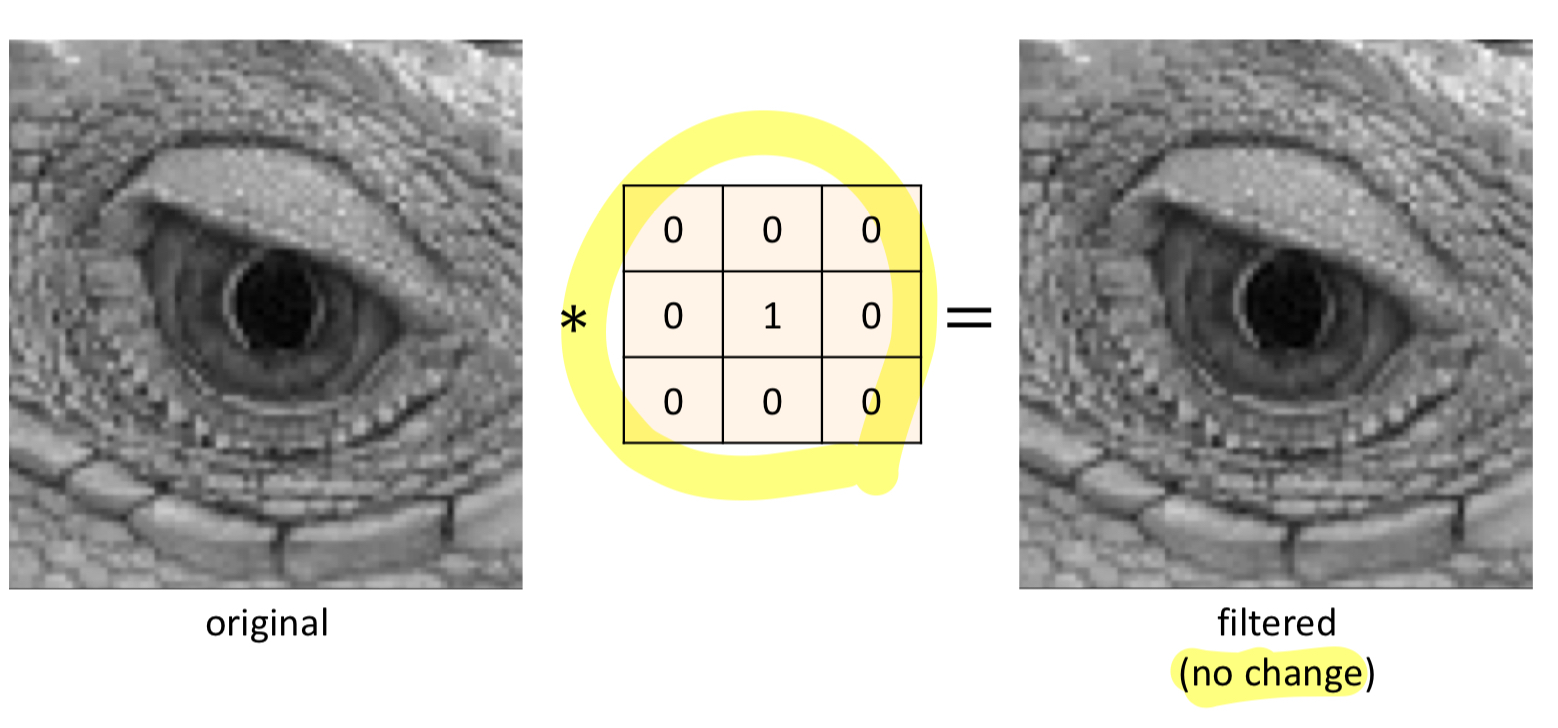
shift right by 1 pixel kernel

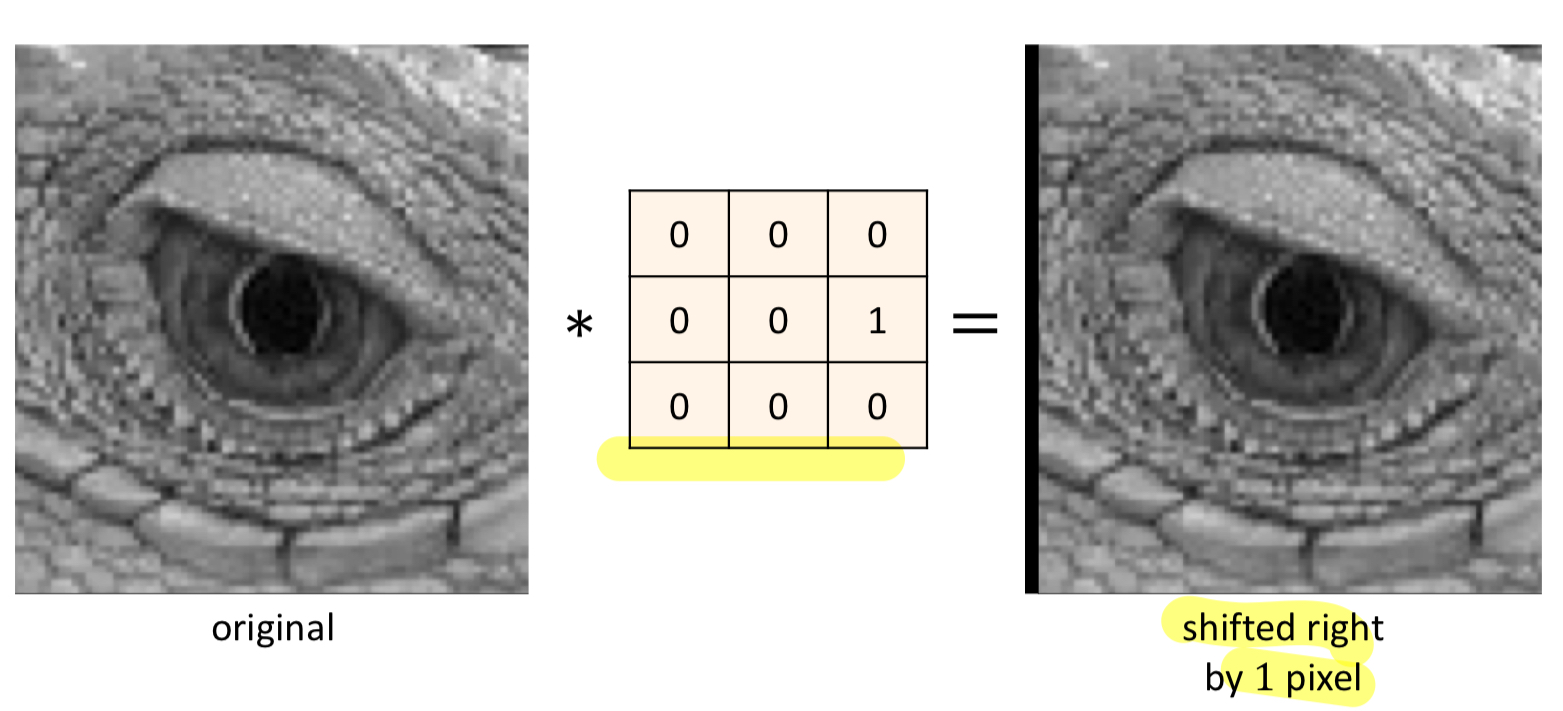
moving average kernel (3x3 average blur kernel)

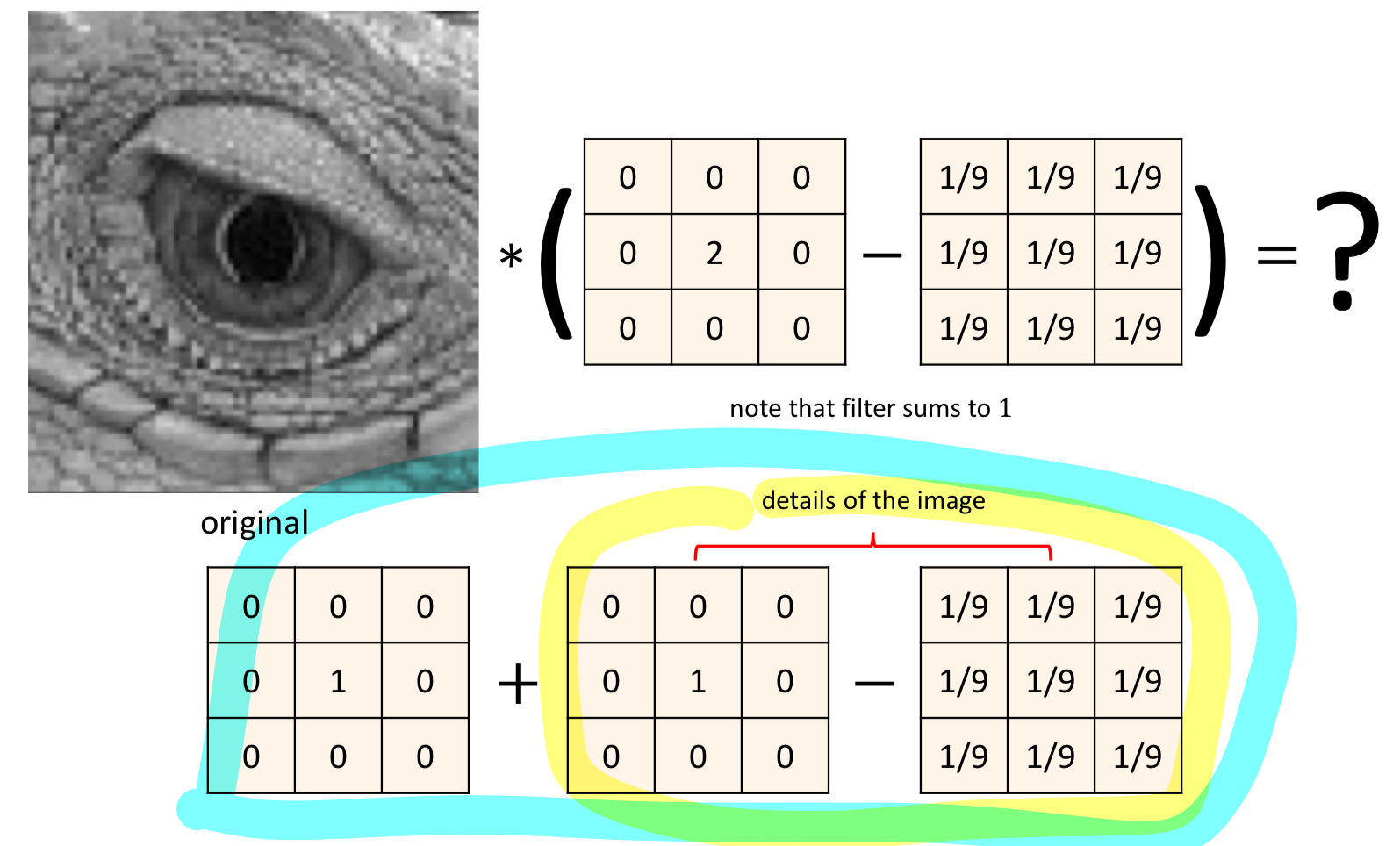
sharpening filter

---

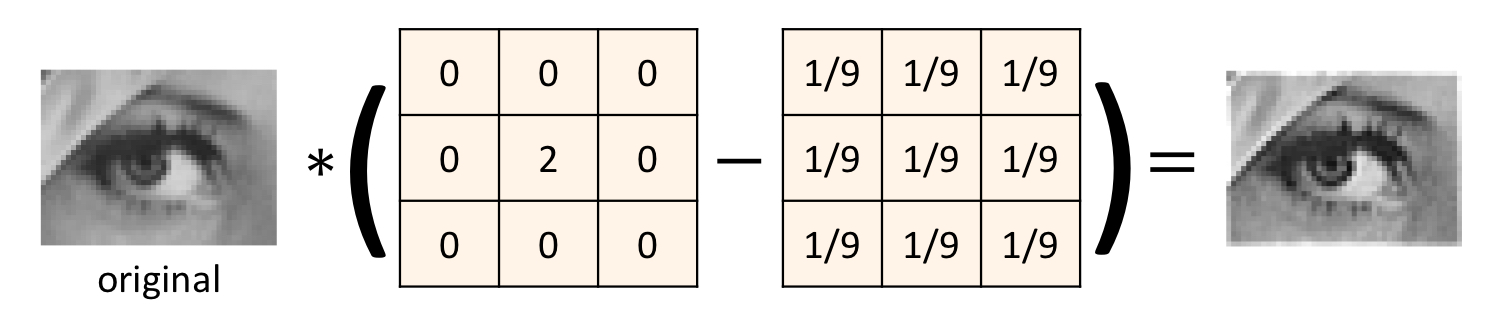
Cross correlation (**)

• cross correlation :
  

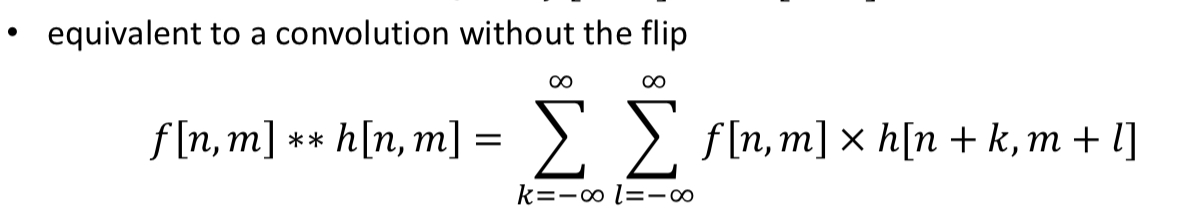
• Properties
  

---

Convolution vs. Cross correlation

• convolution : filtering operation
• correlation : compare the similarity of two set of data