Paper Info

Abstract

• KD는 model compression을 위한 가장 있는 방법 중 하나이다.
  key idea는 teacher model(T)의 knowledge를 student model(S)로 전달하는 것이다.
  그러나 기존 방법들은 S와 T의 학습 능력 간의 큰 차이로 인해 degradation(성능 저하)을 겪는다.

• 이러한 문제를 해결하기 위해, 이 논문에서는 residual error based KD를 제안한다.
  이 방법은 assistant model(A)를 도입하여 지식을 추가로 distillation한다.
  구체적으로, S는 T의 feature map을 모방하도록 훈련되며,
  A는 S와 T 간의 residual error를 학습하여 이 과정을 돕는다.
  이를 통해 S와 A는 서로 보완하며 T로부터 더 나은 knowledge를 얻는다.
  또한 우리는 총 computational cost를 증가시키지 않고 주어진 model에서 S와 A를 도출하는 효과적인 방법을 고안했다.
  광범위한 실험을 통해 우리의 접근 방식이 CIFAR-100과 ImageNet에서 SOTA를 능가하는 결과를 달성하고, adversarial samples에 대해 strong robustness를 유지한다는 것을 보여준다.

1. Introduction

• T에서 S로 효과적인 knowledge transfer를 달성하기 위해, 많은 시도들이 있있다.
  하지만, 아직 해결되긴 멀었다.
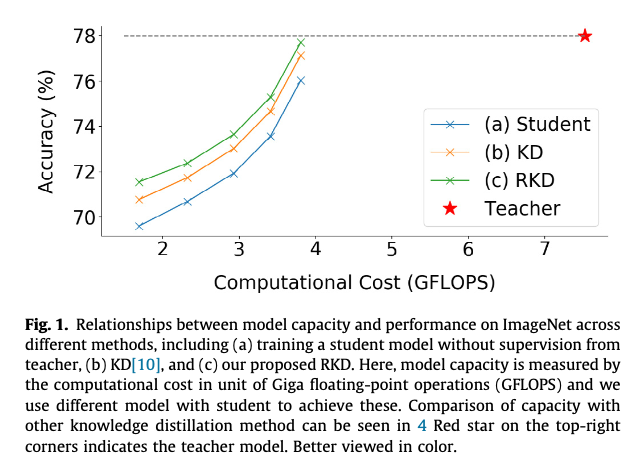  Figure 1.에서 볼 수 있듯이, KD(orange line)는 student(blue line)의 성능을 향상시키는 것을 돕는다.
  하지만 여전히 teacher(dashed grey line)와는 상당한 성능 차이가 있다.
  이는 두 가지 이유가 있다.

  1. S는 T보다 much weaker representation ability를 갖는다.
     Figure 1에서 볼 수 있듯이,
     S의 capacity를 증가시키면 성능이 점진적으로 T에 근접할 수 있지만,
     S와 T의 model size 차이 때문에 student는 well-trained teacher로부터 knowledge를 완전히 습득할 수 없다.
  2. T 내부의 knowledge를 효과적으로 distillation할 방법이 부족하다.
     기존의 KD 방법들은 일반적으로 하나의 teacher가 하나의 student를 supervise하는 방식으로, one-to-one learning이 이루어진다.
     즉, distillation 과정은 S가 T를 모방하도록 optimized될 때 한 번만 발생한다. (Figure.2(a)참조)
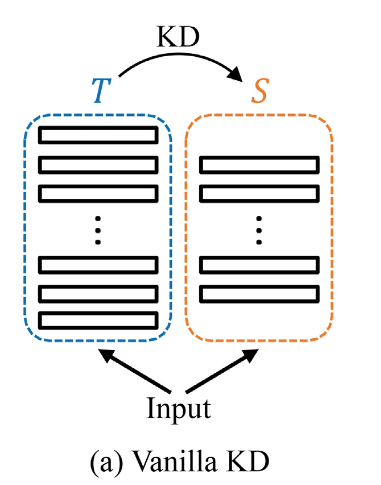     S와 T의 capacity차이가 크다는 것을 고려할 때, 이러한 one-time(1회성) transfer scheme은 어느 정도의 information lost를 야기한다.

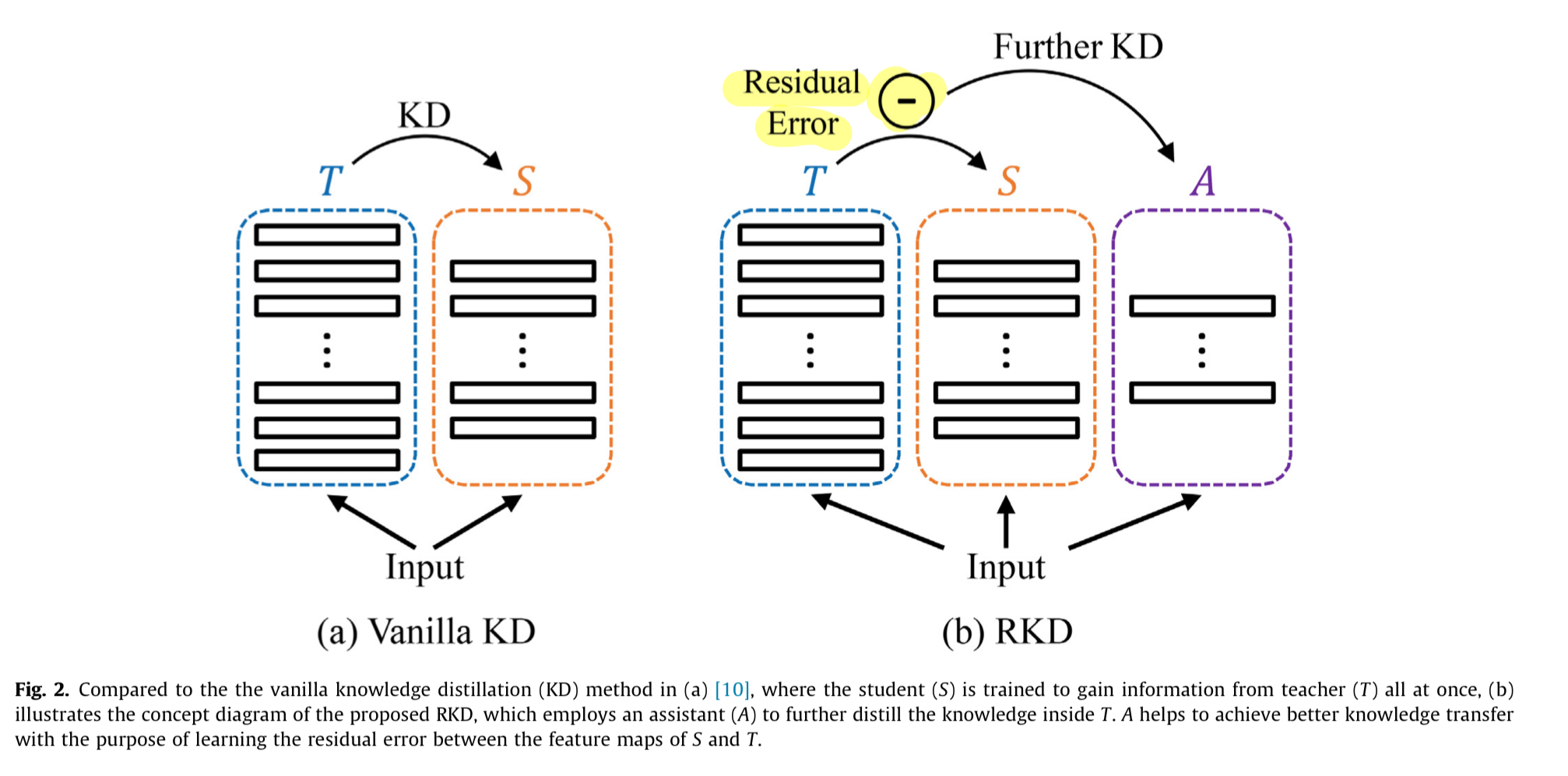
• knowledge transfer 과정을 완화하기 위해, 우리는 Residual error based Knowledge Distillation(RKD)라는 새로운 방법을 제안한다.
  이 방법은 KD 과정에서 assistant model (A)를 도입하여 S가 T로부터 더 나은 knowledge를 얻을 수 있도록 돕는다.
  RKD의 concept diagram은 Fig. 2(b)에 나와있다.
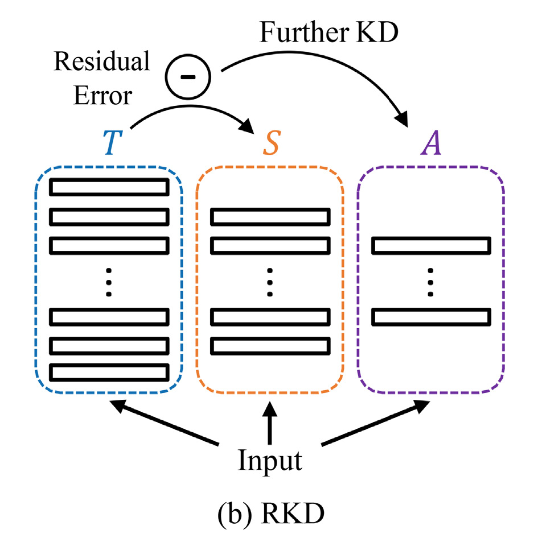  구체적으로, 이 연구에서는 feature map을 knowledge로 취급하며, S는 T와 동일한 feature map을 생성하는 것을 목표로 훈련된다.
  student가 idea mimicking(이상적인 모방)을 달성하는 대신,
  우리는 additional model A를 도입하여 S와 T의 feature map 사이의 residual error를 학습하도록 한다.
  그런 다음 S의 output feature map에 A가 학습한 residual error를 더하여 실제로 사용된다.
  이러한 transfer 방식을 통해 final feature map은 T와 더 구별할 수 없게 되어, S와 T 간의 성능 격차가 좁혀진다. (Fig.1 참조)

• 본 연구의 contribution은 다음과 같이 요약된다 :

  • 우리는 기존의 KD에 assistant model을 추가하여 확장한 새로운 model compression 방법인 RKD를 제안한다.
    이전 방법들이 a single round of KD를 수행하는 것과 달리, RKD는 A가 S와 T 사이의 residual error를 학습하도록 훈련하여 knowledge를 두 번 distillation한다.
    이를 통해 A는 S가 T로부터 학습하지 못한 정보를 포착하여 보다 완전한 knowledge transfer를 가능하게 한다.
    또한 residual error를 학습하는 개념은 기존 KD 방법들의 성능을 향상시키는 데에도 도움을 줄 수 있다.
  • 우리는 기존 model을 두 개의 하위 model로 분리하여 각각 S와 A로 활용하는 방법을 제안한다.
    이를 통해 S와 A를 합친 전체 model의 크기는 증가하지 않아, 다른 방법들과의 공정한 비교가 가능하다.
    실험적으로 A가 S의 model 크기 대비 약 1/10 정도의 lightweight model로 residual error를 완벽히 모방하는 것만으로 충분하다는 것을 증명했다.
    A로 인해 computational cost의 증가가 거의 없는데 반해, S는 A의 도움으로 큰 성능 향상을 얻게 된다.

2. Related Work

2.1. Knowledge Distillation

2.1.1. Knowledge type

• Hinton et al. [10]은 T가 생성한 soft label, 예를 들어 classification probability같은 것이 richer information을 제공한다고 주장.
  최신 연구[21]은 KD 작업에서 feature map을 직접 모방하는 것이 효과적임을 입증했다.
  이와 유사하게, 본 연구에서도 feature map을 knowledge로 활용하며, 이는 feature map 간의 residual error가 명확하게 정의될 수 있기 때문이다.
  그러나 본 연구에서 제안한 RKD는 차이점이 있다.
  residual error를 계산할 방법이 있다면 attention map과 같은 다른 유형의 knowledge와도 함께 작동할 수 있다는 점이다.

2.1.2. Transferring strategy

• [15]는 FitNets을 제안했는데, T와 S에서 각각 hint layer와 guided layer를 선택한다.
  hint layer를 supervision으로 삼아 guided layer를 학습시킴으로써,
  S를 scratch training하는 것보다 더 나은 initialization을 얻을 수 있다.
  ... 이외에도 여러 transferring strategy가 존재...
  하지만 위 모든 방법들은 하나의 model, S를 사용하여 T로부터 학습하며, knowledge는 한 번만 distill된다.
  S와 T의 학습 능력 차이를 고려할 때, S가 이러한 1회성 transfer를 통해 T의 성능을 재현할 만큼 충분한 정보를 얻을 수 있다는 보장은 없다.
  반대로, 우리는 assistant model(A)를 추가하여 knowledge를 한 번 더 증류할 것을 제안한다.
  A는 knowledge를 두 번째로 distillation하여 T에서 S로 정보를 더 충분히 transfer할 수 있게 돕는다.

2.2. Residual learning

• residual learning은 [6]에 의해 처음으로 CNN에 도입된 효과적인 학습 방식이다.
  일반적으로, 이 방법의 core thought는 어떠한 reference 없이 target function을 직접 optimizing하는 것보다 residual을 학습하는 것이 더 쉽다는 hypothesis에 기반을 두고 있다.
  이는 coarser(identity branch)와 finer(residual branch)으로 해결하는 coarse-to-fine idea와 일치한다.
  본 연구에서는 이 원칙을 KD task에 도입했다.
  이전 연구들이 T로부터 S(coarser)를 optimize하는 데 집중한 반면,
  우리가 제안한 RKD는 A(finer)가 S와 T 사이의 residual error를 학습하도록 한다.
  이를 통해 A는 S의 feature map을 세밀하게 다듬어 T의 knowledge가 보다 완전하게 distillation되도록 한다.
  우리가 아는 한, model compression에서 residual learning을 활용한 것은 이번 연구가 처음이다.

3. Residual error based knowledge distillation

• 우리는 두 model, 즉 S와 A를 사용하여 T로부터 complementary manner(상호보완적인 방식)로 knowledge를 얻는 RKD를 수식화했다. (Fig.3 M.1 참조)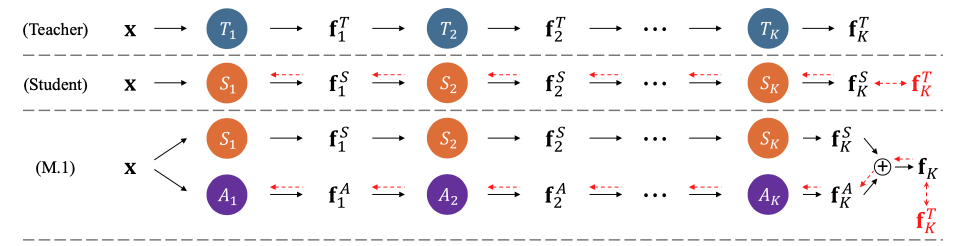knowledge를 더 정확하게 transfer하고 RKD의 train을 더 쉽게 만들기 위해, 우리는 이 framework의 두 가지 variants도 제안한다.
  progressive learning scheme(M.2)와 A를 S에 통합하는 end-to-end training scheme(M.3)이 포함된다.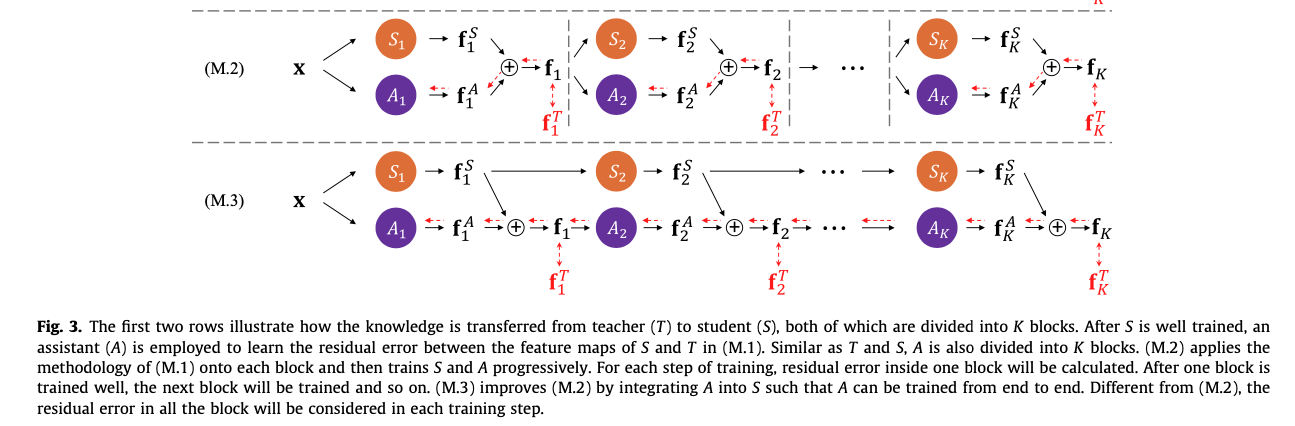또한, pre-designed model에서 S와 A의 network structures를 도출하는 효율적인 방법을 탐구했으며,
  A를 도입한 후에도 total computational cost가 증가하지 않도록 했다.
  더 자세한 내용은 다음 section에서 논의될 것..

3.1. Knowledge Distillation

• KD는 일반적으로 student model S가 well-trained teacher model T로부터 학습하여 T의 predictive capability를 재현하는 것을 목표로 한다.
  즉, image-label pair (x, y)가 주어지면, T는 prediction $\hat{y}^T=T(x)$을 만들어 내고,
  S는 $\hat{y}^T$와 유사한 결과를 만들어내는 것을 목표로 학습되어진다.
  여기서, S가 만들어낸 prediction을 $\hat{y}^S = S(x)$라고 denote한다.

• 이 목표를 이루기 위해, KD는 CNN model에 포함된 정보를 추출하는 방법을 탐구하고, S의 정보를 T의 정보와 최대한 가깝게 밀착시키는 것을 목표로 한다.
  따라서 KD는 다음과 같이 formulated될 수 있다 :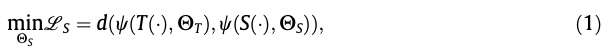여기서 $\Theta_T$와 $\Theta_S$는 각각 T와 S의 trainable parameters이다.
  $w(.,.)$는 특정 model의 knowledge를 정의하는 데 도움을 주는 함수이며,
  $d(.,.)$는 두 model의 knowledge 간 거리를 측정하는 metric이다.

• Eq. (1)에서 update되는 것은 오직 $\Theta_S$뿐이며, T는 이미 ground-truth data로 optimized되었다고 가정한다.
  classification task의 경우, Cross-entropy loss가 objective function으로 사용된다 :$N$은 #categories,
  $y$는 ground-truth label을 나타내는 N-dimensional one-hot vector이며,
  $\hat{y}^T$는 T가 예측한 soft probability이다.

3.2. Residual learning with A (M.1)

• 본 연구에서, 우리는 CNN model의 feature map을 근복적인 knowledge로 다룰 것이다.
  일반적으로, model을 a set of blocks로 나눌 수 있고,
  각 block의 output은 hidden feature map으로 간주된다.

• 예를 들어, T는 $K$개의 blocks으로 이루어져 있다. $\{T_i()\}^K_{i=1}$
  그리고 $K$개 block의 output에 대응하는, $K$개의 hidden feature maps을 갖는다. $\{f_i^T\}^K_{i=1}$
  T는 또한 final feature map $f^T_K$를 soft label prediction $\hat{y}^T$로 변환하는 softmax function에 의해 activated되는 FC layer = classifier를 갖는다.
  하지만, [21]에서 영감을 받아, T와 S의 classifier는 동일한 구조와 동일한 learning capacity를 공유하므로 KD 과정에서 제외된다.
  (마지막 fc layer는 T와 S가 똑같으니까 제외한다는 말인듯)
  T와 마찬가지로 S도 $K$개의 block으로 나뉜다.
  따라서 T에서 S로 knowledge를 transfer하기 위해 Eq. (1)은 다음과 같이 simplified된다 :
  $||.||_2$는 두 tensor 간의 $l_2$ distance를 denotes한다.
  다른 말로, $S$는 $T$와 동일한 feature map을 생성하려고 시도하여, 유사한 성능을 달성하고자 한다.
  하지만 S와 T의 representation capacities의 상당한 차이를 고려할 때, S만으로는 T의 feature map의 내재된 knowledge를 충분히 잘 맞추는 것이 쉽지 않을 것이다.
  이 문제를 해결하기 위해, 우리는 assistant model(A)를 도입하여 S가 이 mimicking process를 더 잘 수행할 수 있도록 돕는다.
  이는 Fig. 3(M.1)에 있다.
  구체적으로, $A$ 또한 $K$개의 blocks으로 구성된 $\{A_i(.)\}^K_{i=1}$로, image $x$를 input으로 사용하며,
  loss function과 함께 $f^S_K$와 $f^T_K$ 사이의 residual error를 학습하도록 optimized된다 :$A$와 $S$가 각각 optimized된 후, residual error가 더해진 feature map $f_K = S_K + A_K$가 최종적으로 inference에 참여된다.
  (극소량이라고 하지만.. A라는 model parameter가 추가되어 같이 학습하는 구조인듯)
  A를 도입함으로써 knowledge를 두 단게에 걸쳐 distillation된다.
  첫 번째로, S는 Eq. (3)을 통해 T의 hidden feature map을 모방하도록 optimized되고,
  그 후 A의 parameter는 residual learning stage에서 Eq. (4)을 사용하여 S가 학습한 feature map을 정제하도록 update된다.
  (각 단계에서 $S$ 또는 $A$ 중 하나의 model만 훈련된다는 점을 유의하자.)
  비록 별도로 훈련되지만, $A$는 $S$와 동일한 목표를 공유하며, 이는 $f_K$를 통해 $f_K^T$를 근사하는 것이다.
  결과적으로, A는 첫 번째 단계에서 놓친 정보를 보완하여 S의 성능을 향상시킨다.

3.3. Progressive learning (M.2)

3.4. Integrating A into S (M.3)

3.5. Separating A from S

3.6. Implementation details

Critique

• assistant model A를 도입하여 S와 T의 feature map 사이의 residual error를 학습하도록 유도한다고 하는데,
  지적 1 : 이 논문에서 최종적으로 하고자 하는게 T와 S 사이의 residual error를 줄이도록 학습하여 KD를 하는 것인데,
  residual error를 줄인다고 S의 성능이 좋아질 것으로 확신하는가? 그렇다면, 왜 그렇게 생각하는지? 뒷받침 자료(납득할 만한 설명과 실험 등 필요)

중단

• 이 논문에서 residual error의 의미 :
  teacher의 intermediate feature map $f^T$와 student의 intermediate feature map $f^S$ 을 이용하여 feature mimicking type의 KD를 수행한다.
  즉, $loss(f^T, f^S)$를 최소화하는 것을 목표로 한다.
  여기서 $f^T$와 $f^S$ 사이의 좁혀야 하는 error를 residual error로 정의하고,
  이 error를 더욱 더 잘 좁히기 위해 추가적인 assistant model(A)을 사용하여 KD를 두 번 수행한다.
  

• 내가 이 논문을 선택하여 읽게 된 이유는 residual이 아래 그림의 residual인줄 알았다.
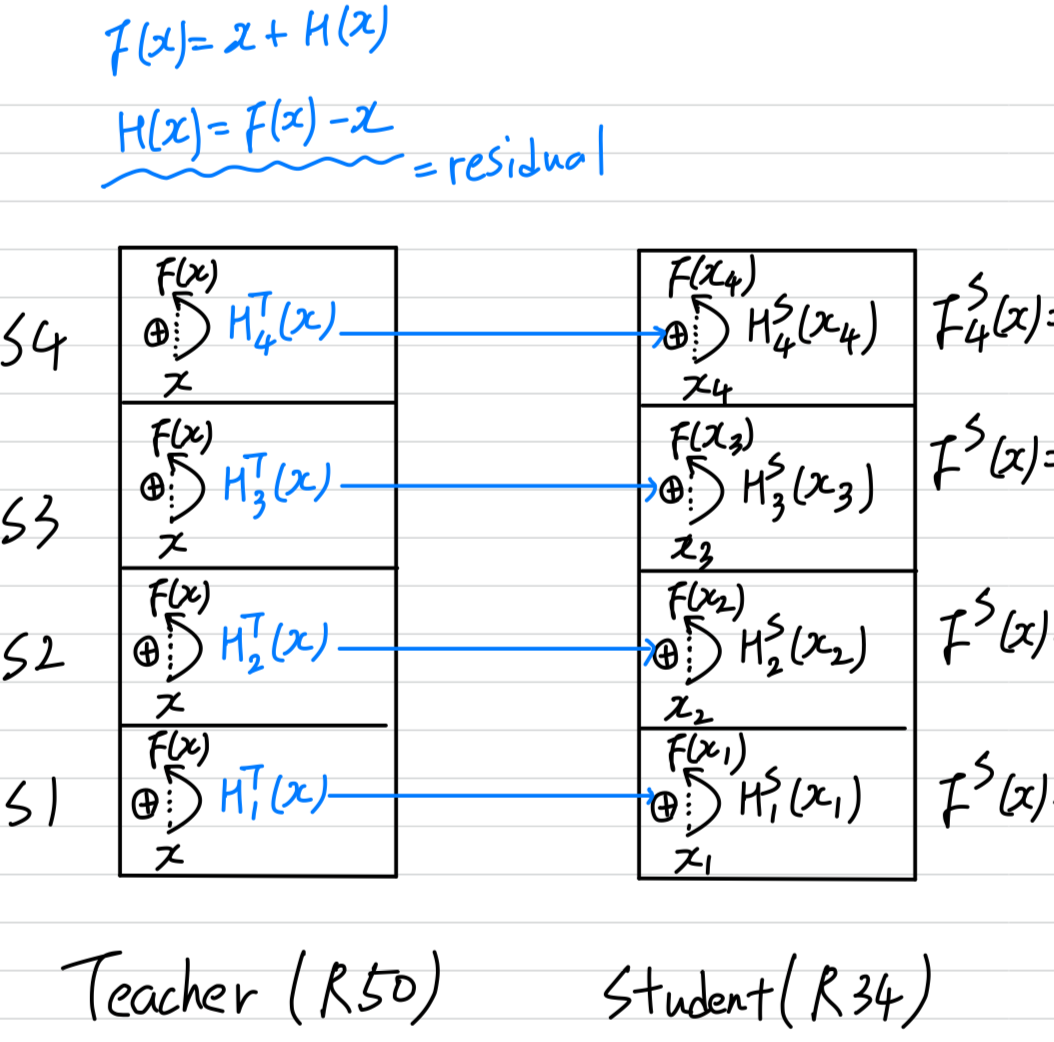  내가 현재 생각하고 있는 아이디어는 아래 그림의 residual을 이용하여 KD를 할 수 있는 방법이었기 때문에
  이 논문은 내가 얻고자 하는 직관과는 거리가 멀어서 3.2.까지만 읽고 그만 읽는다....