신경망 학습 (2)

Hyungseop Lee·2023년 3월 7일

경사법(경사 하강법)

기계학습 문제 대부분은 학습 단계에서 최적의 Parameter를 찾아낸다.
신경망 역시 최적의 Parameter(가중치, 편향)을 학습 시에 찾아야 한다.

여기에서 최적이란 Loss Function이 최솟값이 될 때의 Paramter값이다.

하지만 일반적인 문제의 Loss Function은 매우 복잡하다.
매개변수 공간이 광대하여 어디에 최솟값이 되는 곳인지 짐작할 수 없다.
이런 상황에서 기울기를 이용해 함수의 최솟값(또는 가능한 작은 값)을 찾으려는 것이 경사법이다.

경사법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동한다.
그런 다음 이동한 곳에서도 마찬가지로 기울기를 구하고, 또 그 기울어진 방향으로 나아가기를 반복한다.
이렇게 해서 함수의 값을 점차 줄이는 것이 경사 하강법(Gradient Descent Method)이다.

주의할 점

각 지점에서 함수의 값을 낮추는 방안을 제시하는 지표가 기울기라는 것인데,
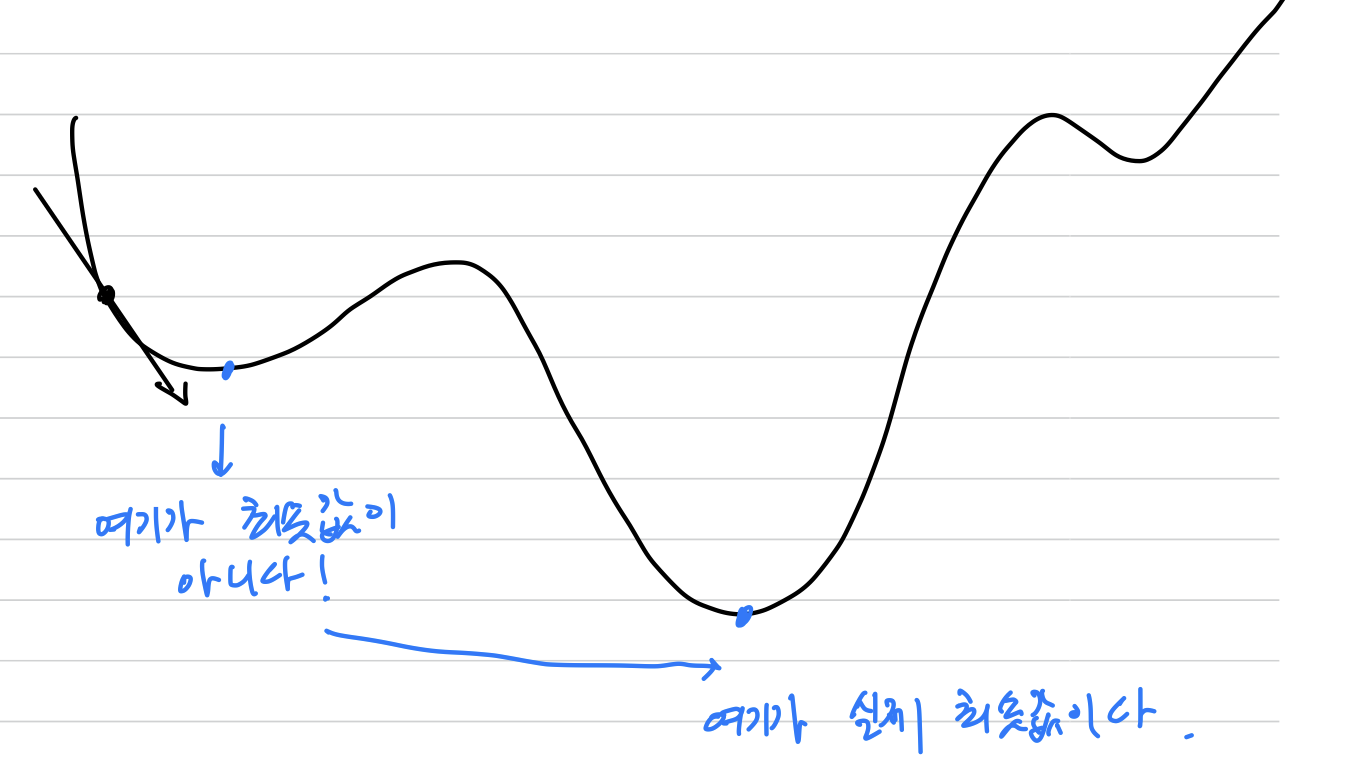
하지만 기울기가 가리키는 곳에 정말 함수의 최솟값이 있는지,
즉 그쪽이 정말로 나아갈 방향인지는 보장할 수 없다.

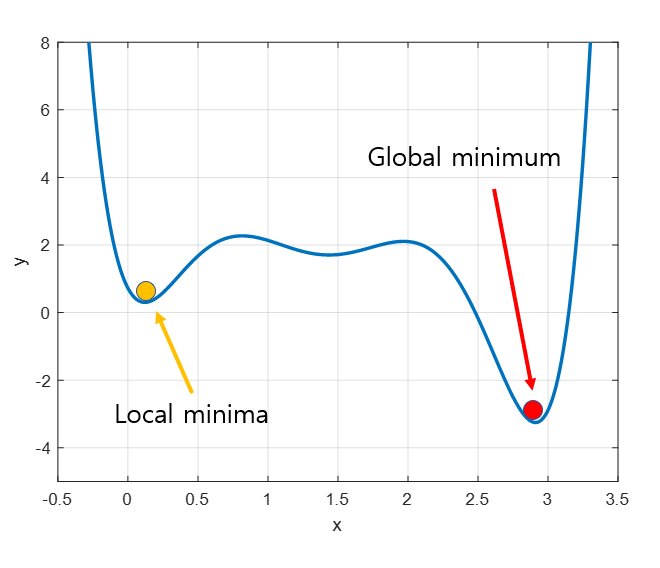
함수가 극솟값, 최솟값, 안장점이 되는 장소에서는 기울기가 0이 된다.

극솟값(한정된 범위에서의 최솟값인 점)

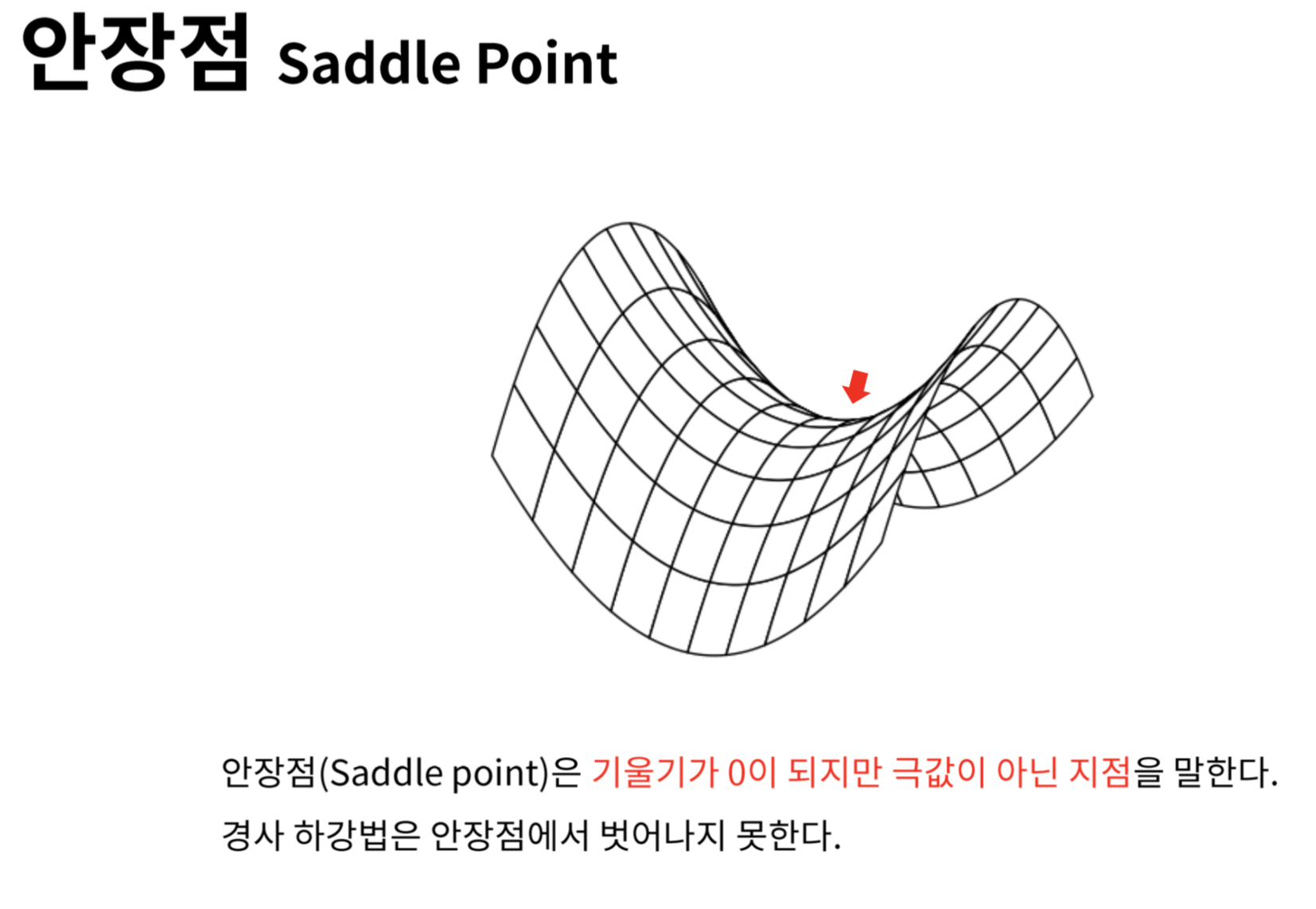
안장점(어느 방향에서 보면 극댓값이고 다른 방향에서 보면 극솟값이 되는 점)

경사법은 기울기가 0인 장소를 찾지만 그것이 반드시 최솟값이라고는 할 수 없다.
극솟값이나 안장점일 가능성이 있기 때문이다.
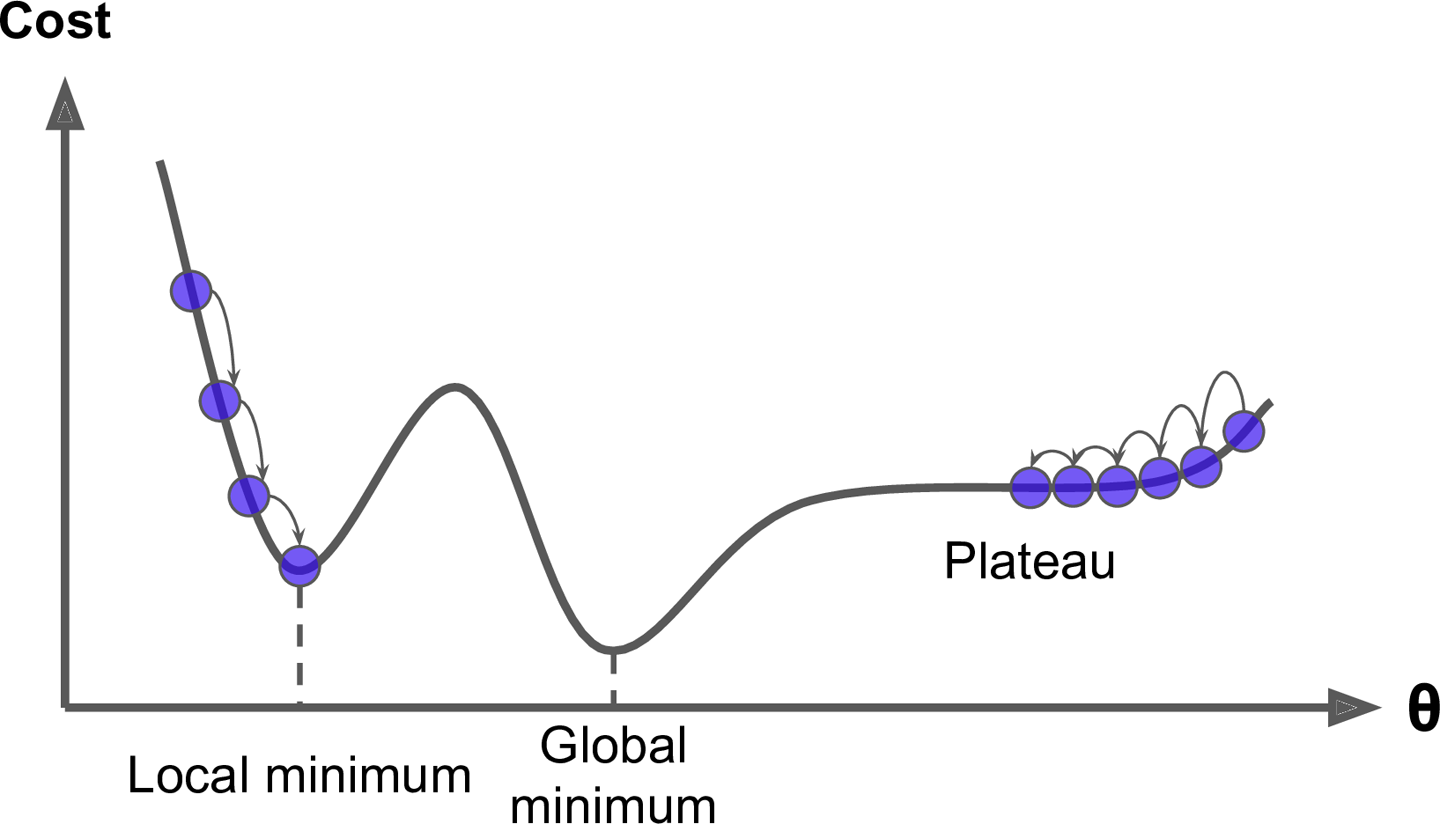
또한 평평한 곳으로 파고들면서 고원(Plateau)이라 하는, 학습이 진행되지 않는 정체기에 빠질 수 있다.

극솟값
안장점
고원(Plateau, 플레토)

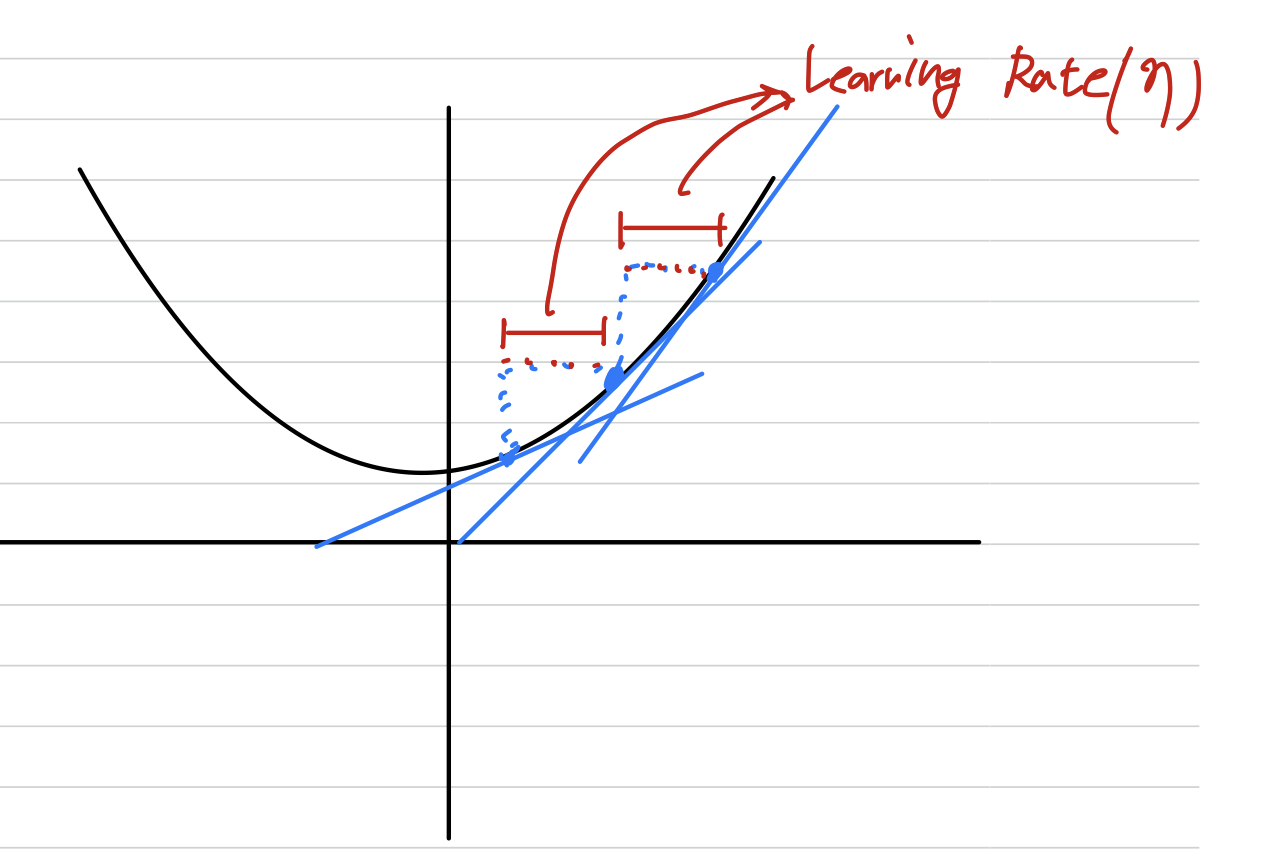
경사법 수식

$\eta$ (eta, 에타) : Learning rate == 학습률 == 갱신하는 양
➡️ 한 번의 학습으로 얼만큼 학습해야 할지, 즉 매개변수 값을 얼마나 갱신하느냐를 정하는 것.

학습률과 같은 매개변수를 Hyper Paramter(초매개변수)라고 한다. 이는 가중치와 편향 같은 매개변수와는 성질이 다른 매개변수이다.
신경망의 가중치 Parameter는 훈련 데이터와 학습 알고리즘에 의해서 자동으로 획득되는 매개변수인 반면, 학습률 같은 Hyper Paramter는 사람이 직접 설정해야하는 매개변수이다.
일반적으로 Hyper Paramter들은 여러 후보 값 중에서 시험을 통해 가장 잘 학습하는 값을 찾는 과정을 거쳐야 한다.

학습률 값은 0.01이나 0.001 등 미리 특정 값으로 정해두어야 한다.
일반적으로 이 값이 너무 크거나 너무 작으면 좋은 장소를 찾아갈 수 없다.

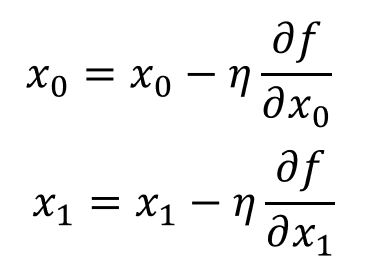
경사법 구현

# f : 최적화하려는 함수
# init_x : 초기값
# lr : 학습률 == learning rate(Hyper Parameter)
# step_num : 경사법 반복 횟수
def gradient_descent(f, init_x, lr=0.01, step_num=100) :
    x = init_x
    
    for i in range(step_num) :
        grad = numerical_gradient(f, x) # 수치 미분 결과 반환 함수(앞서 정의함)
        x -= lr * grad                  # 경사법 수식
    return x

문제 : 경사법으로 $f(x_0, x_1) = x_0^2 + x_1^2$ 의 최솟값을 구하라.

def function_2(x) :
    return x[0]**2 + x[1]**2

# 초기값 임의 설정
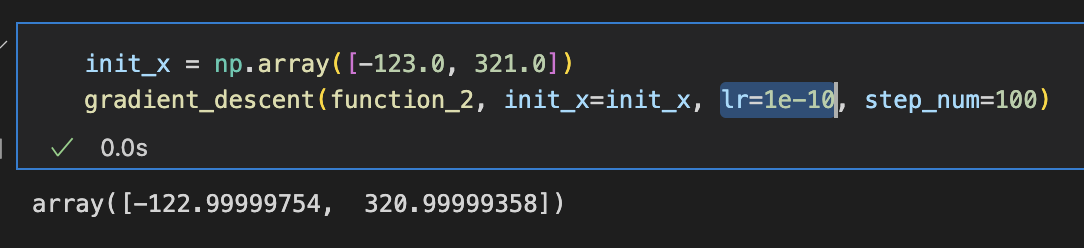
init_x = np.array([-123.0, 321.0])
print(gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100))

최솟값 결과 (-2.50555425e-08 6.53888548e-08)
➡️ (0, 0)과 매우 가까운 결과.

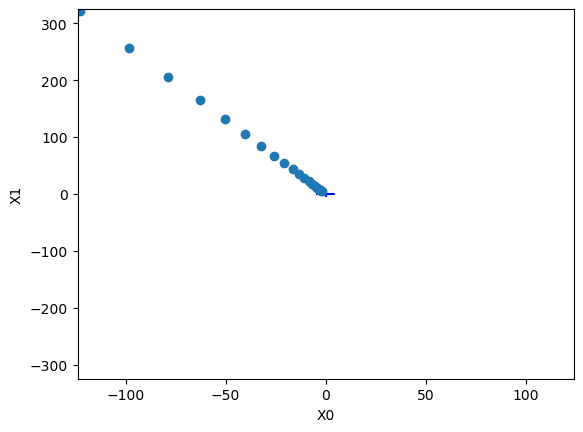
위 그림은 경사법의 갱신 과정을 나타낸 그래프이다.
값이 가장 낮은 장소인 (0, 0)에 가까워지고 있는 것을 확인할 수 있다.

Learning Rate(Hyper Parameter) 설정 시 주의사항

학습률이 너무 크거나, 너무 작으면 좋은 결과를 얻을 수 없다.

학습률이 너무 클 경우

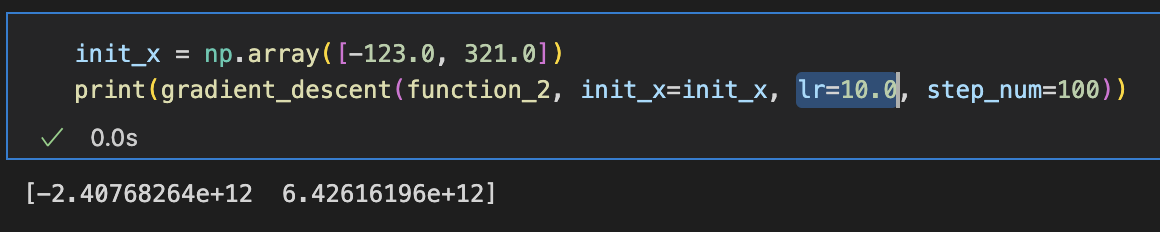
학습률이 너무 작을 경우

신경망에서의 기울기

Loss Function값을 Weight Matrix로 편미분(Weight에 대한 Loss의 기울기)

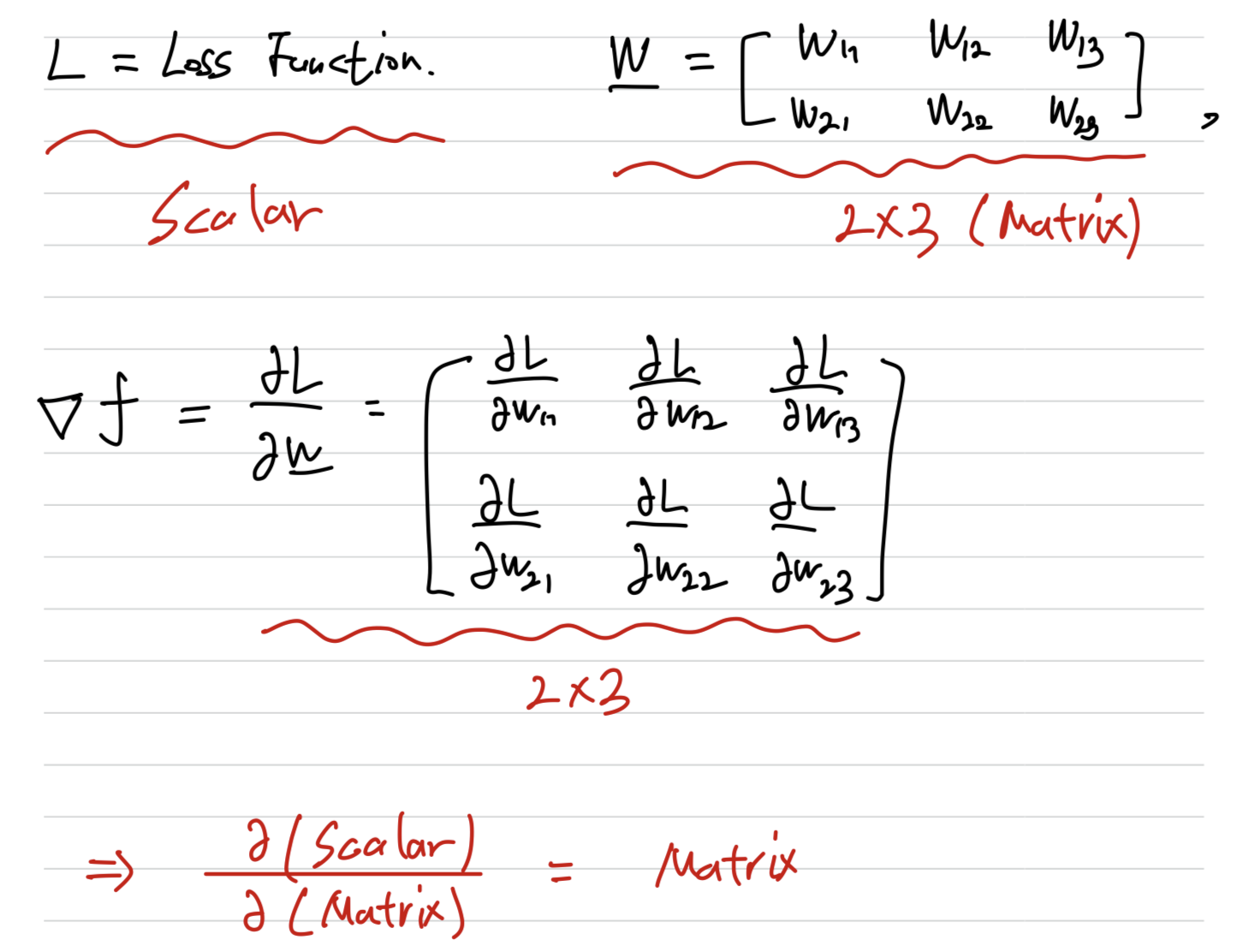
$L$ : Loss Function
$W$ : Weight(가중치)

$\frac{\partial L}{\partial W}$ : Weight값 각각을 조금씩 변경하였을 때 Loss Function의 변화량

💡 포인트 : Scalar를 Matrix에 대하여 편미분한 결과는 Matrix이다(Matrix Shape이 똑같음)

신경망에서의 기울기 구현

아래와 같은 simple한 Neural Net을 구현하고,
SimpleNet의 Loss와 기울기를 출력한다.

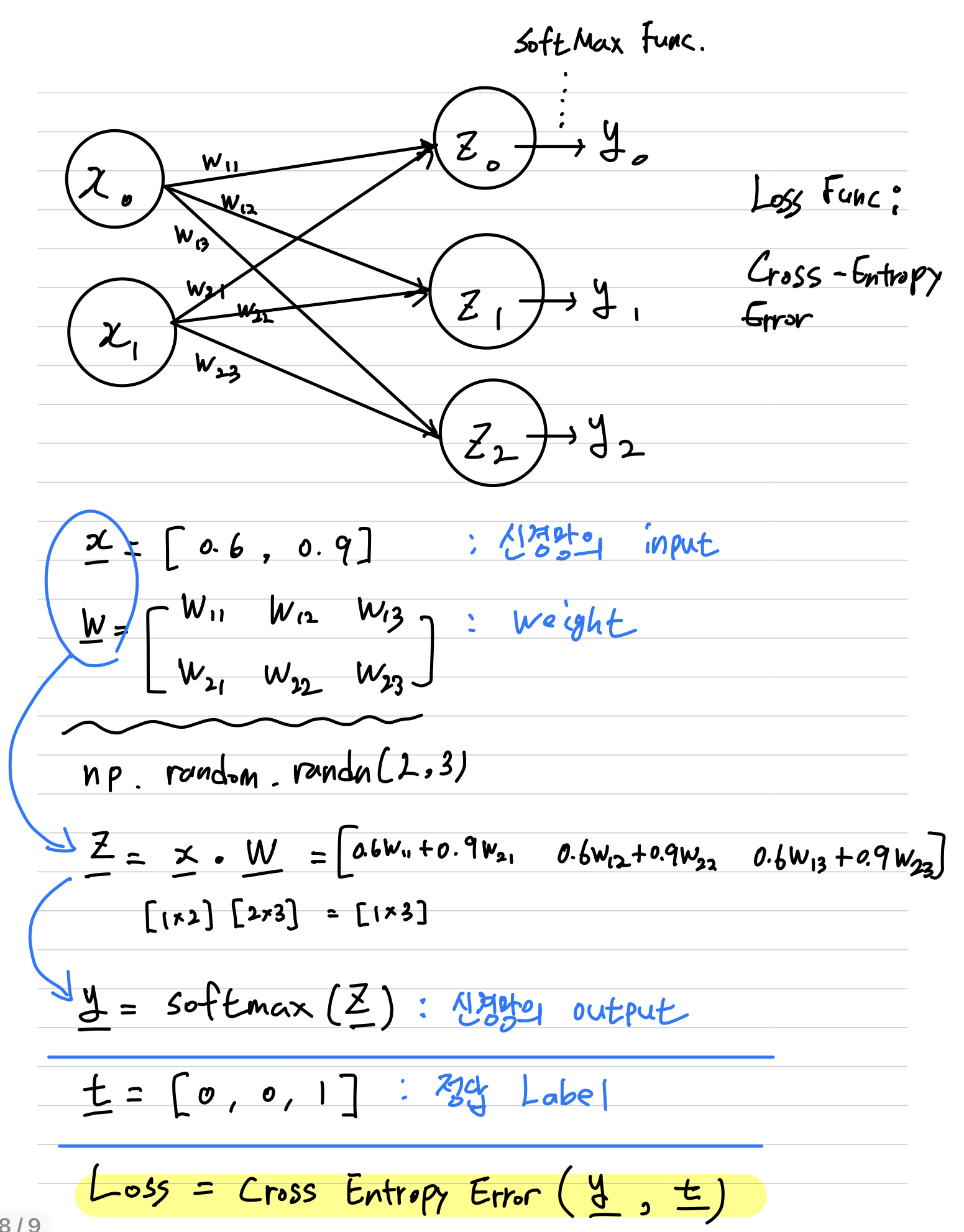
신경망을 생성할 Class 생성

import sys, os
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient

class simpleNet : 
    def __init__(self) -> None:
        self.W = np.random.randn(2, 3) # Weight, 정규분포로 초기화
    def predict(self, x) :
        return np.dot(x, self.W) 
    def loss(self, x, t) :
        print("신경망의 input(x) : \n" + str(x))
        print("신경망의 Weight(W) : \n" + str(self.W), end='\n\n')
        
        z = self.predict(x)  # x*W
        print("신경망에서 예측한 정답(z) \n: " + str(z))
        print(np.argmax(z))
        
        print("실제 정답 label(t) \n: " + str(t), end='\n\n')
        
        y = softmax(z)       
        print("신경망의 예측에 softmax 적용한 최종 output(y) : \n" + str(y), end='\n\n')
        
        loss = cross_entropy_error(y, t) # 손실함수로 cross entropy 사용
        print("이 신경망의 Loss Function으로 Cross-Entropy Eror(y, t)를 반환합니다.")
        return loss

Class를 통해 1개의 신경망 객체 생성 후 Loss Function값 출력

net = simpleNet() # 신경망 생성

x = np.array([0.6, 0.9]) 
t = np.array([0, 0, 1])  # 실제 정답 레이블

print('CEE Loss Function값 : '+ str(net.loss(x, t)))

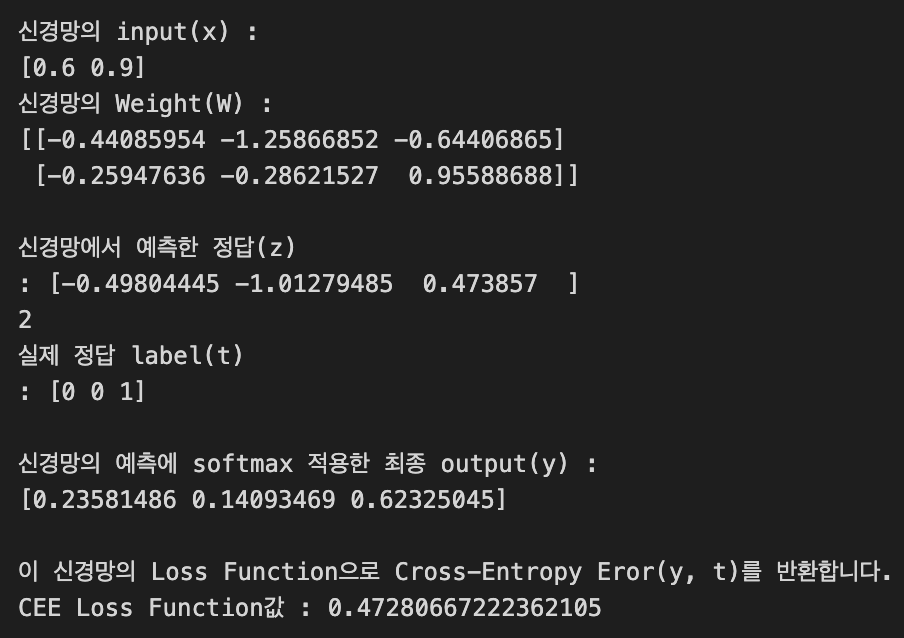
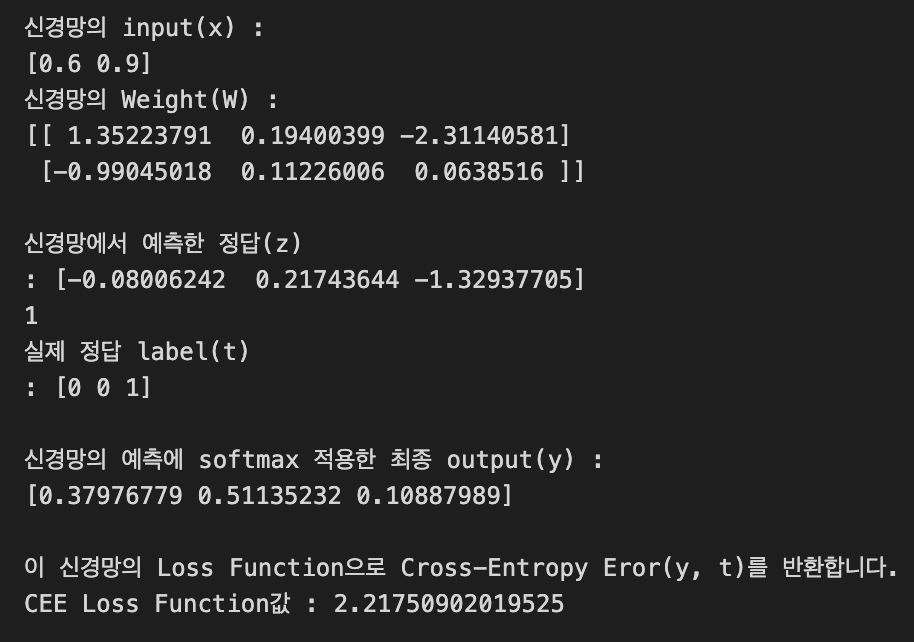
아래는 출력인데,
신경망에서 예측한 정답(y)과 실제 정답(t)이 일치했을 때,
Loss Function값이 낮은 것을 확인할 수 있다.
신경망에서 예측한 정답(y)과 실제 정답(t)이 불일치했을 때,
Loss Function값이 높은 것을 확인할 수 있다.

(핵심) Weight에 대한 Loss의 기울기 구하기

net = simpleNet() # 신경망 생성
x = np.array([0.6, 0.9]) # 신경망 input
t = np.array([0, 0, 1])  # 실제 정답 레이블
f = lambda l : net.loss(x, t) # 신경망의 Loss값

dW = numerical_gradient(f, net.W) # Weight에 대한 Loss의 기울기 구하기
print(dW)