[1][GNN][GCN] Laplacian matrix
1. Intro
- 주어진 그래프를 spectral 도메인으로 해석하는데 laplacian matrix를 사용한다.
- laplacian matrix가 무엇이길래, graph를 표현하는데 쓰이는걸까?
- laplacian matrix의 의미에 대해 알아보자.
2. laplacian matrix란?
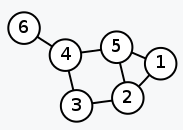
2-1 Adjacaemcy matrix

- Adjacaemcy matrix는 그래프의 연결관계를 표현한 행렬이다.
- 위에서 처럼 두 노드(i,j)가 연결되어 있으면 로 아니면 이 되는 행렬이다.
2-2 Degree matrix

- Degree matrix는 한 노드에 연결된 엣지의 개수이다.
2-3 laplacian matrix

- laplacian matrix는 Degree matrix - Adjacaemcy matrix로 정의된다.
- : Laplacian matrix
- : Degree matrix
- : Adjacaemcy matrix
3. Smoothness
- laplacian matrix는 graph의 smoothness를 측정할 수 있다.
- 이게 무슨말일까?
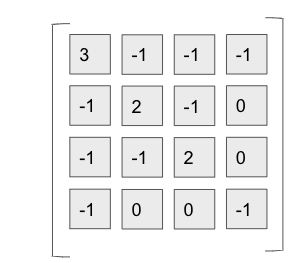
- laplacian matrix()가 아래 처럼 주어졌다고 생각해보자.
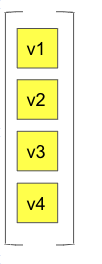
- 이때 각 노드의 값을 (v1, v2, v3, v4) = 로 표현해보자.
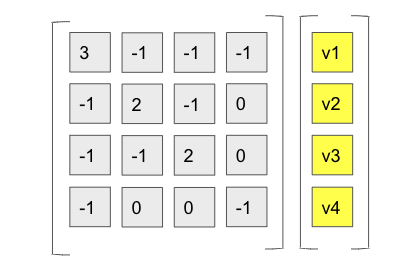
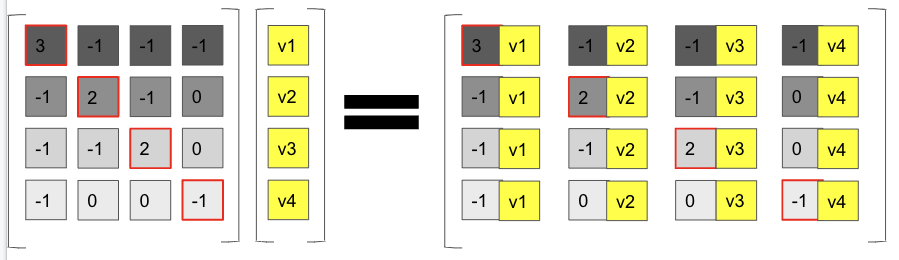
- 그러면 는 다음과 같이 된다.
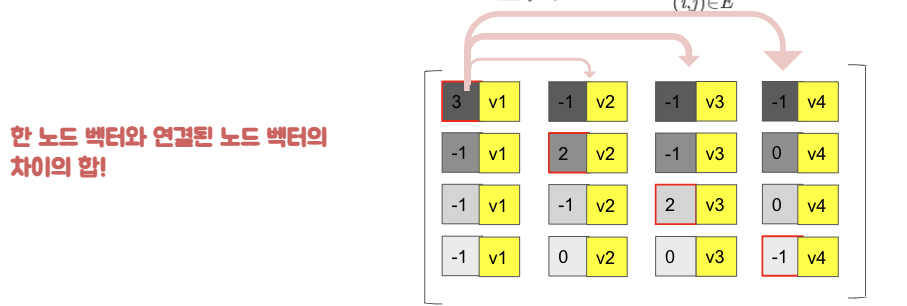
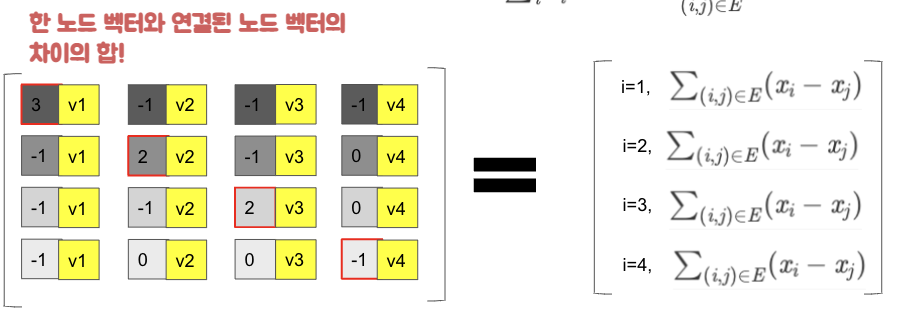
- 위와 같은 과정으로 인해 는 각 노드가 이웃노드와 얼마나 차이가 나는지 측정하게 된다.
- 는 여기서 아래와 같이 된다.
- 즉 는 각 노드와 이웃노드 사이의 차이 제곱의 합이 된다.
- 만약 이웃노드끼리 값이 비슷하다면 는 값이 작을 것이다.
- 만약 이웃노드이지만 값이 크게 다르다면 는 값이 클 것이다.
- 이러한 성질로인해 laplacian matrix는 smoothness를 측정할 수 있다.
4. eigenvalue decomposition
- Lapalacian matrix는 대각성분으로 기준으로 좌우가 대칭이여서 Positive semi-definite matrix이고 성질로 인해 모든 고유값이 실수이다.
- (eigenvalue decomposition이 뭔지 잘 모른다면 10시간정도는 들여서 따로 공부하는 것이 좋을 것 같다.)
- 따라서 다음과 같은 고유값 분해가 가능하다.
- 라플라시안 matrix의 eigenvalue가 작을수록 그래프에 대한 의미를 많이 가지고 있을 수 있다.
- 이어지는 다음글에서 laplacian matrix의 eigenvalue의 의미와 eigenvector를 활용한 graph의 spectral representation에 대해서 알아보자..



글 잘 읽었습니다!
이어지는 다음 글은 어디서 확인할 수 있나요?